26.2.2 二次函数y=ax2+bx+c的图像、性质与系数的关系(课件)九年级数学(华师大版)(共25张PPT)
文档属性
| 名称 | 26.2.2 二次函数y=ax2+bx+c的图像、性质与系数的关系(课件)九年级数学(华师大版)(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 17:45:09 | ||
图片预览






文档简介
(共25张PPT)
第6课时 二次函数y=ax2+bx+c的图像、性质与系数的关系
温故知新
请你说说它的图像和性质吧!
温故知新
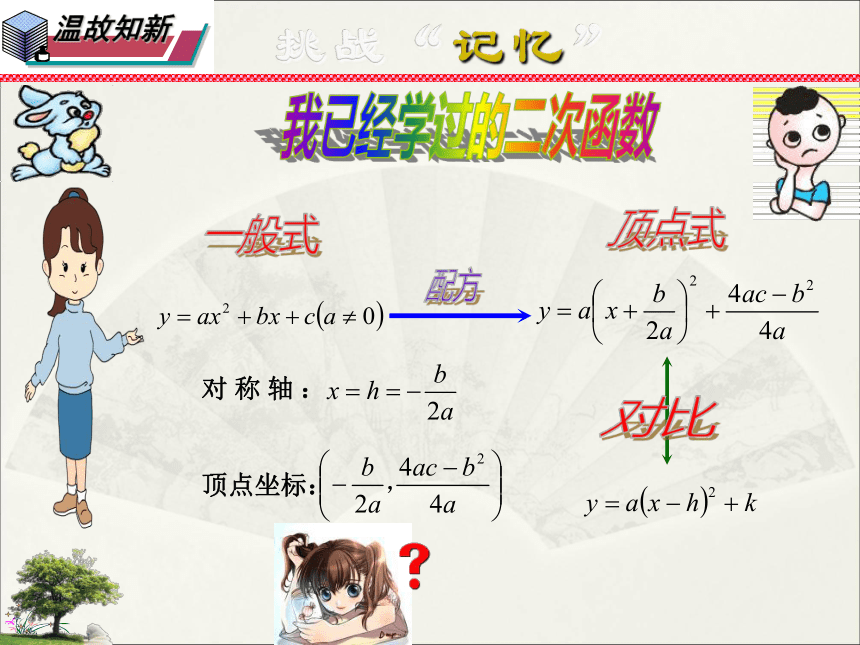
对称轴:
顶点坐标:
情境激疑
想一想:一次函数 的图象与系数之间有何关系?
k决定直线的倾斜方向,决定与y轴的交点情况
二次函数 的图像与系数间有何关系呢?
九年级(下)
新华东师大版第26章 二次函数
探究发现
问题1:二次函数 的二次项系数a有何作用?
x
y
O
直线
如果a>0时,开口向上,当 时,
探究发现
问题1:二次函数 的二次项系数a有何作用?
x
y
O
直线
如果a<0时,开口向下,当 时,
综上所述,a决定抛物线的开口方向:
当a>0 ,抛物线开口向上;当a<0,抛物线开口向下;
当 , 函数取得最值,最值
探究发现
问题2:二次函数 中a,b的作用?
x
y
O
直线
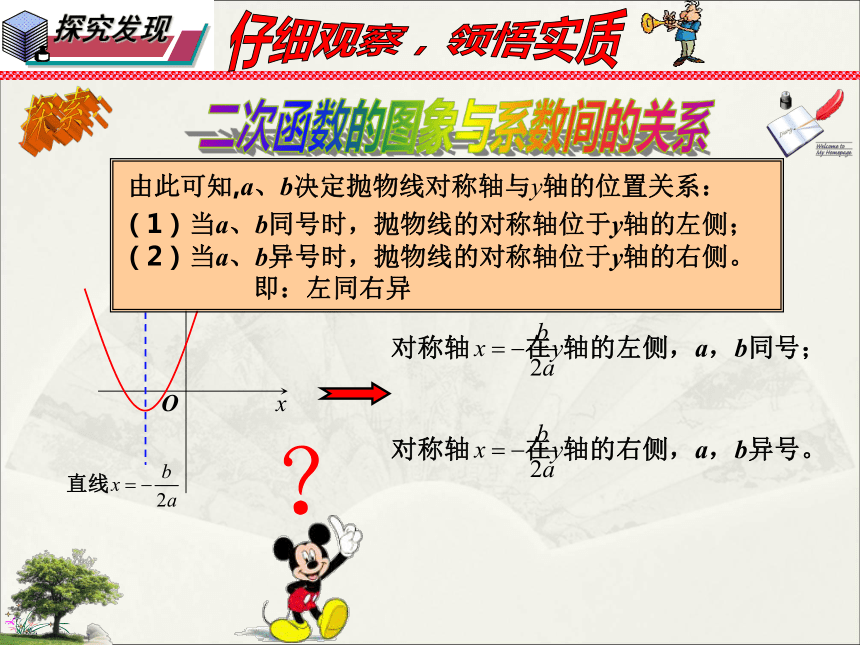
对称轴 在y轴的左侧,a,b同号;
对称轴 在y轴的右侧,a,b异号。
由此可知,a、b决定抛物线对称轴与y轴的位置关系:
(1)当a、b同号时,抛物线的对称轴位于y轴的左侧;
(2)当a、b异号时,抛物线的对称轴位于y轴的右侧。
即:左同右异
?
探究发现
问题3:二次函数 中c有何作用?
x
y
O
当c>0时,抛物线与y轴的交点在y轴的正半轴;
当c=0时,抛物线与y轴的交点为原点;
当c<0时,抛物线与y轴的交点在y轴的负半轴;
由此可知,c决定抛物线与y轴的交点情况:
(1)当c>0时,抛物线与y轴的交点在y轴的正半轴;
(2)当c=0时,抛物线与y轴的交点为原点;
(3)当c<0时,抛物线与y轴的交点在y轴的负半轴。
探究发现
问题4:二次函数 中a,b,c的作用?
x
y
O
当△>0时,抛物线与x轴有两个不同的交点;
当△=0时,抛物线与x轴只有一个交点;
当△<0时,抛物线与x轴没有交点。
由此可知,a,b,c决定抛物线与x轴的交点情况:
(1)当△>0时,抛物线与x轴有两个不同的交点;
(2)当△=0时,抛物线与x轴有且只有一个交点;
(3)当△<0时,抛物线与x轴没有交点。
探究发现
(Ⅰ)a决定抛物线的开口方向:
①当a>0时,抛物线的开口向上,抛物线有最低点,函数有最小值,
当 时, ;
②当a<0时,抛物线的开口向下,抛物线有最高点,函数有最大值,
当 时, ;
(Ⅱ)a、b共同决定对称轴的相对于y轴的位置:
①当a、b同号时,对称轴 在y轴的左侧;
②当a、b异号时,对称轴 在y轴的右侧。
探究发现
(Ⅲ)c决定抛物线与y轴的交点情况:
①当c>0时,抛物线与y轴的交点在y轴的正半轴;
③当c<0时,抛物线与y轴的交点在y轴的负半轴。
(Ⅳ)a、b、c共同决定抛物线与x轴的交点情况:
①当 时,抛物线与x轴有两个不同的交点;
②当c =0时,抛物线经过原点;
②当 时,抛物线与x轴只有一个交点;
③当 时,抛物线与x轴没有交点。
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
你是怎样考虑的?
例 2
如图是二次函数 的图象,对于下列说法:
① , ② , ③ , ④ ,
⑤ , ⑥ , ⑦ .
正确的有 .(填写序号)
x
y
O
2
1
-1
-2
③
⑦
数 学 活 动 室
学 以 致 用
1.已知二次函数y=ax2+bx+c的图像如图所示,下列结论:
①a+b+c<0,②a-b+c>0; ③ abc>0;④b=2a
其中正确的个数为 ( )
A、4个 B、3个 C、2个 D、1个
y
1
x
-1
O
A
学以致用
例 3
二次函数 与一次函数 在同一坐标系内的
大致图象是( )
x
y
o
x
y
x
y
x
y
O
C
D
B
A
O
O
C
数 学 活 动 室
学 以 致 用
2.若一次函数 的图象经过第二、三、四象限,则二次函数
的大致图象是( )
x
y
O
A
-3
x
y
O
B
-3
x
y
O
C
-3
x
y
O
D
-3
C
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.2
P 18
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
第6课时 二次函数y=ax2+bx+c的图像、性质与系数的关系
温故知新
请你说说它的图像和性质吧!
温故知新
对称轴:
顶点坐标:
情境激疑
想一想:一次函数 的图象与系数之间有何关系?
k决定直线的倾斜方向,决定与y轴的交点情况
二次函数 的图像与系数间有何关系呢?
九年级(下)
新华东师大版第26章 二次函数
探究发现
问题1:二次函数 的二次项系数a有何作用?
x
y
O
直线
如果a>0时,开口向上,当 时,
探究发现
问题1:二次函数 的二次项系数a有何作用?
x
y
O
直线
如果a<0时,开口向下,当 时,
综上所述,a决定抛物线的开口方向:
当a>0 ,抛物线开口向上;当a<0,抛物线开口向下;
当 , 函数取得最值,最值
探究发现
问题2:二次函数 中a,b的作用?
x
y
O
直线
对称轴 在y轴的左侧,a,b同号;
对称轴 在y轴的右侧,a,b异号。
由此可知,a、b决定抛物线对称轴与y轴的位置关系:
(1)当a、b同号时,抛物线的对称轴位于y轴的左侧;
(2)当a、b异号时,抛物线的对称轴位于y轴的右侧。
即:左同右异
?
探究发现
问题3:二次函数 中c有何作用?
x
y
O
当c>0时,抛物线与y轴的交点在y轴的正半轴;
当c=0时,抛物线与y轴的交点为原点;
当c<0时,抛物线与y轴的交点在y轴的负半轴;
由此可知,c决定抛物线与y轴的交点情况:
(1)当c>0时,抛物线与y轴的交点在y轴的正半轴;
(2)当c=0时,抛物线与y轴的交点为原点;
(3)当c<0时,抛物线与y轴的交点在y轴的负半轴。
探究发现
问题4:二次函数 中a,b,c的作用?
x
y
O
当△>0时,抛物线与x轴有两个不同的交点;
当△=0时,抛物线与x轴只有一个交点;
当△<0时,抛物线与x轴没有交点。
由此可知,a,b,c决定抛物线与x轴的交点情况:
(1)当△>0时,抛物线与x轴有两个不同的交点;
(2)当△=0时,抛物线与x轴有且只有一个交点;
(3)当△<0时,抛物线与x轴没有交点。
探究发现
(Ⅰ)a决定抛物线的开口方向:
①当a>0时,抛物线的开口向上,抛物线有最低点,函数有最小值,
当 时, ;
②当a<0时,抛物线的开口向下,抛物线有最高点,函数有最大值,
当 时, ;
(Ⅱ)a、b共同决定对称轴的相对于y轴的位置:
①当a、b同号时,对称轴 在y轴的左侧;
②当a、b异号时,对称轴 在y轴的右侧。
探究发现
(Ⅲ)c决定抛物线与y轴的交点情况:
①当c>0时,抛物线与y轴的交点在y轴的正半轴;
③当c<0时,抛物线与y轴的交点在y轴的负半轴。
(Ⅳ)a、b、c共同决定抛物线与x轴的交点情况:
①当 时,抛物线与x轴有两个不同的交点;
②当c =0时,抛物线经过原点;
②当 时,抛物线与x轴只有一个交点;
③当 时,抛物线与x轴没有交点。
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
例 1
抛物线 如图所示,试确定a、b、c、△的符号:
x
O
y
学以致用
你是怎样考虑的?
例 2
如图是二次函数 的图象,对于下列说法:
① , ② , ③ , ④ ,
⑤ , ⑥ , ⑦ .
正确的有 .(填写序号)
x
y
O
2
1
-1
-2
③
⑦
数 学 活 动 室
学 以 致 用
1.已知二次函数y=ax2+bx+c的图像如图所示,下列结论:
①a+b+c<0,②a-b+c>0; ③ abc>0;④b=2a
其中正确的个数为 ( )
A、4个 B、3个 C、2个 D、1个
y
1
x
-1
O
A
学以致用
例 3
二次函数 与一次函数 在同一坐标系内的
大致图象是( )
x
y
o
x
y
x
y
x
y
O
C
D
B
A
O
O
C
数 学 活 动 室
学 以 致 用
2.若一次函数 的图象经过第二、三、四象限,则二次函数
的大致图象是( )
x
y
O
A
-3
x
y
O
B
-3
x
y
O
C
-3
x
y
O
D
-3
C
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.2
P 18
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
