2.6直角三角形的性质与判定(共15张PPT)
文档属性
| 名称 | 2.6直角三角形的性质与判定(共15张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 213.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
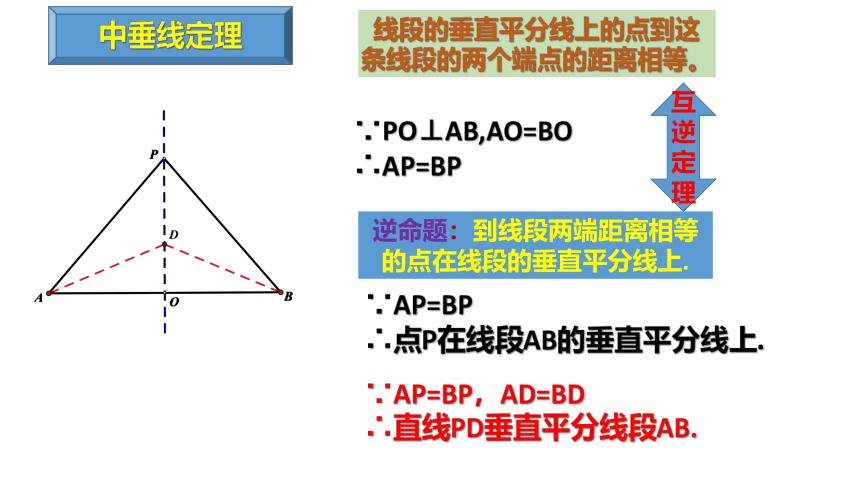
错题订正---作业本①P17第6题
已知:如图,D是▲ABC内部一点,且DB=DC,∠ABD=∠ACD.求证:AB=AC
证明:∵DB=DC
∴∠DBC=∠DCB(在三角形中,等边对等角)
∵∠ABD=∠ACD
∴∠ABD+∠DBC=∠ACD+∠DCB
即∠ABC=∠ACB
∴AB=AC(在三角形中,等角对等边)
强调:若要证明两条线段相等,可分两种情况讨论:
①当两条边在两个三角形中时,可通过证明全等来解决;
②当两条边可在一个三角形中时,可借助等角对等边进行处理.
对应训练---《课时特训》P34第11题
已知:如图,在▲ABC中,D是BC上一点,DA平分∠EDC,且∠E=∠B.DE=DC求证:AB=AC
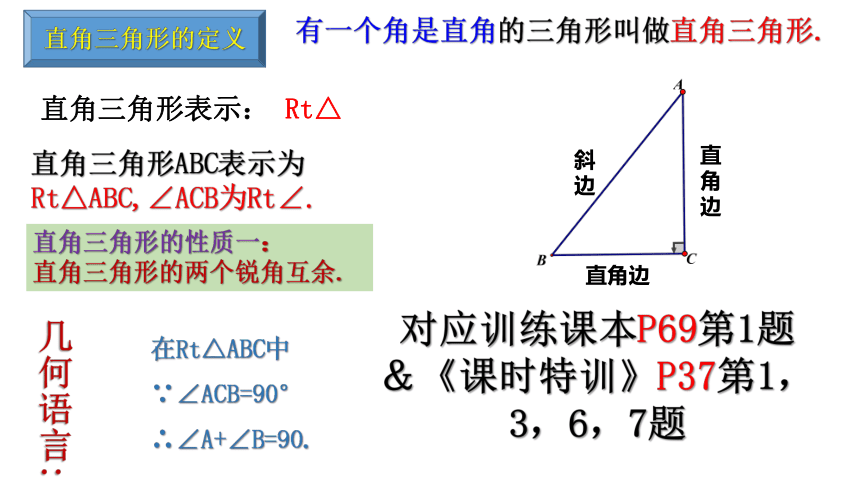
线段的垂直平分线上的点到这条线段的两个端点的距离相等。
逆命题:到线段两端距离相等的点在线段的垂直平分线上.
互逆定理
∵PO⊥AB,AO=BO
∴AP=BP
∵AP=BP
∴点P在线段AB的垂直平分线上.
中垂线定理
∵AP=BP,AD=BD
∴直线PD垂直平分线段AB.
2.5.1直角三角形的性质
有一个角是直角的三角形叫做直角三角形.
直角三角形表示: Rt△
直角三角形ABC表示为Rt△ABC,∠ACB为Rt∠.
直角三角形的定义
斜边
直角边
直角边
在Rt△ABC中
∵∠ACB=90°
∴∠A+∠B=90.
直角三角形的性质一:
直角三角形的两个锐角互余.
对应训练课本P69第1题
&《课时特训》P37第1,3,6,7题
几何语言:
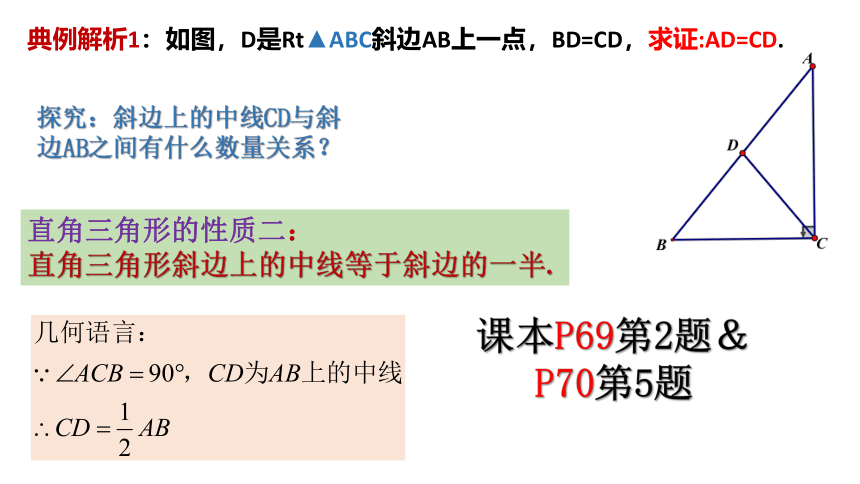
典例解析1:如图,D是Rt▲ABC斜边AB上一点,BD=CD,求证:AD=CD.
探究:斜边上的中线CD与斜边AB之间有什么数量关系?
直角三角形的性质二:
直角三角形斜边上的中线等于斜边的一半.
课本P69第2题&P70第5题
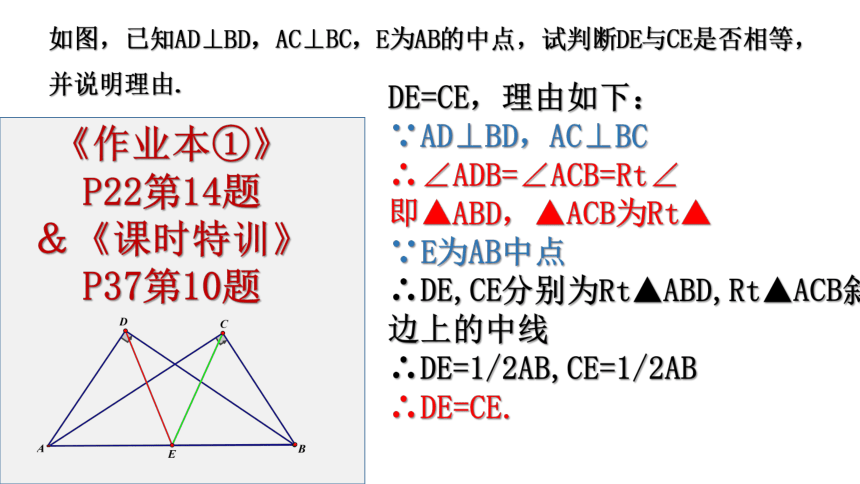
如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由.
DE=CE,理由如下:
∵AD⊥BD,AC⊥BC
∴∠ADB=∠ACB=Rt∠
即▲ABD,▲ACB为Rt▲
∵E为AB中点
∴DE,CE分别为Rt▲ABD,Rt▲ACB斜边上的中线
∴DE=1/2AB,CE=1/2AB
∴DE=CE.
《作业本①》P22第14题
&《课时特训》P37第10题
30°
在Rt三角形ABC中,∠ACB=Rt∠.CD为斜边AB上的中线,若∠A=30°,你能求出那些角的度数?
(1) △BDC是什么三角形?
(2) 此时BC与AC有什么关系?
等边三角形
直角三角形的性质三:
在直角三角形中,30°所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
∴ BC = AB.
《课时特训》P37第8,9题
A
B
C
等腰直角三角形的两个锐角为_____度.
45
两条直角边相等的直角三角形叫做等腰直角三角形.
等腰直角三角形
如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD.请说明理由.
D
《课时特训》P37第13题
2.5.2直角三角形的判定
直 角 三 角 形 的 判 定
直角三角形的判定定理一:
有一个角是直角的三角形是直角三角形.
直角三角形的判定定理二:
有两个角互余的三角形是直角三角形.
直角三角形其他判定方法
直角三角形的判定①:
如果三角形的一个顶点是它的三条高线的交点,那么这个三角形是直角三角形.
典例解析2 已知:如图,CD是三角形ABC的边AB上的中线,CD=1/2AB.求证:三角形ABC是直角三角形
1
2
判断命题“如果一个三角形一条边的中线是这条边的一半,那么这个三角形是直角三角形”是否是真命题.
1
2
直角三角形的判定②:
如果一个三角形一条边的中线是这条边的一半,那么这个三角形是直角三角形.
对应训练《课本P72第5题》
1
2
错题订正---作业本①P17第6题
已知:如图,D是▲ABC内部一点,且DB=DC,∠ABD=∠ACD.求证:AB=AC
证明:∵DB=DC
∴∠DBC=∠DCB(在三角形中,等边对等角)
∵∠ABD=∠ACD
∴∠ABD+∠DBC=∠ACD+∠DCB
即∠ABC=∠ACB
∴AB=AC(在三角形中,等角对等边)
强调:若要证明两条线段相等,可分两种情况讨论:
①当两条边在两个三角形中时,可通过证明全等来解决;
②当两条边可在一个三角形中时,可借助等角对等边进行处理.
对应训练---《课时特训》P34第11题
已知:如图,在▲ABC中,D是BC上一点,DA平分∠EDC,且∠E=∠B.DE=DC求证:AB=AC
线段的垂直平分线上的点到这条线段的两个端点的距离相等。
逆命题:到线段两端距离相等的点在线段的垂直平分线上.
互逆定理
∵PO⊥AB,AO=BO
∴AP=BP
∵AP=BP
∴点P在线段AB的垂直平分线上.
中垂线定理
∵AP=BP,AD=BD
∴直线PD垂直平分线段AB.
2.5.1直角三角形的性质
有一个角是直角的三角形叫做直角三角形.
直角三角形表示: Rt△
直角三角形ABC表示为Rt△ABC,∠ACB为Rt∠.
直角三角形的定义
斜边
直角边
直角边
在Rt△ABC中
∵∠ACB=90°
∴∠A+∠B=90.
直角三角形的性质一:
直角三角形的两个锐角互余.
对应训练课本P69第1题
&《课时特训》P37第1,3,6,7题
几何语言:
典例解析1:如图,D是Rt▲ABC斜边AB上一点,BD=CD,求证:AD=CD.
探究:斜边上的中线CD与斜边AB之间有什么数量关系?
直角三角形的性质二:
直角三角形斜边上的中线等于斜边的一半.
课本P69第2题&P70第5题
如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由.
DE=CE,理由如下:
∵AD⊥BD,AC⊥BC
∴∠ADB=∠ACB=Rt∠
即▲ABD,▲ACB为Rt▲
∵E为AB中点
∴DE,CE分别为Rt▲ABD,Rt▲ACB斜边上的中线
∴DE=1/2AB,CE=1/2AB
∴DE=CE.
《作业本①》P22第14题
&《课时特训》P37第10题
30°
在Rt三角形ABC中,∠ACB=Rt∠.CD为斜边AB上的中线,若∠A=30°,你能求出那些角的度数?
(1) △BDC是什么三角形?
(2) 此时BC与AC有什么关系?
等边三角形
直角三角形的性质三:
在直角三角形中,30°所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
∴ BC = AB.
《课时特训》P37第8,9题
A
B
C
等腰直角三角形的两个锐角为_____度.
45
两条直角边相等的直角三角形叫做等腰直角三角形.
等腰直角三角形
如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD.请说明理由.
D
《课时特训》P37第13题
2.5.2直角三角形的判定
直 角 三 角 形 的 判 定
直角三角形的判定定理一:
有一个角是直角的三角形是直角三角形.
直角三角形的判定定理二:
有两个角互余的三角形是直角三角形.
直角三角形其他判定方法
直角三角形的判定①:
如果三角形的一个顶点是它的三条高线的交点,那么这个三角形是直角三角形.
典例解析2 已知:如图,CD是三角形ABC的边AB上的中线,CD=1/2AB.求证:三角形ABC是直角三角形
1
2
判断命题“如果一个三角形一条边的中线是这条边的一半,那么这个三角形是直角三角形”是否是真命题.
1
2
直角三角形的判定②:
如果一个三角形一条边的中线是这条边的一半,那么这个三角形是直角三角形.
对应训练《课本P72第5题》
1
2
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
