2.7.1探索勾股定理 课件(共23张PPT)
文档属性
| 名称 | 2.7.1探索勾股定理 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 21:52:46 | ||
图片预览




文档简介
(共23张PPT)
2.7.1直角三角形
浙教版 八年级上
新知导入
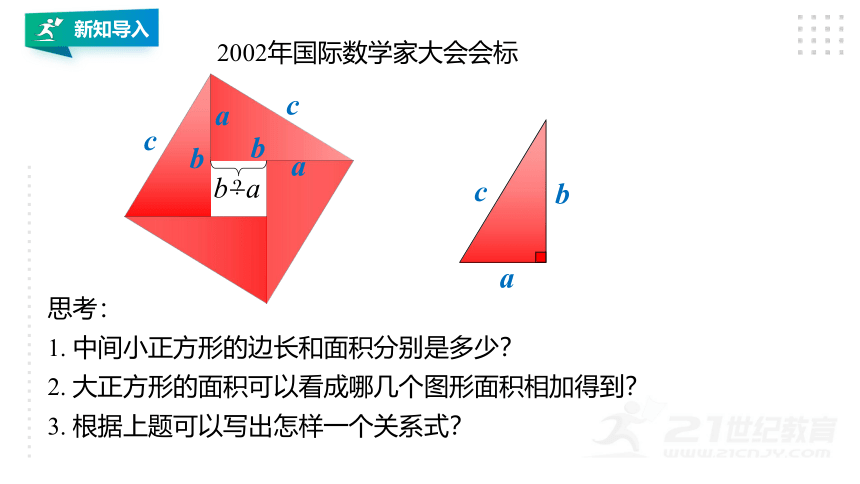
2002年国际数学家大会会标
思考:
1. 中间小正方形的边长和面积分别是多少?
2. 大正方形的面积可以看成哪几个图形面积相加得到?
3. 根据上题可以写出怎样一个关系式?
新知导入
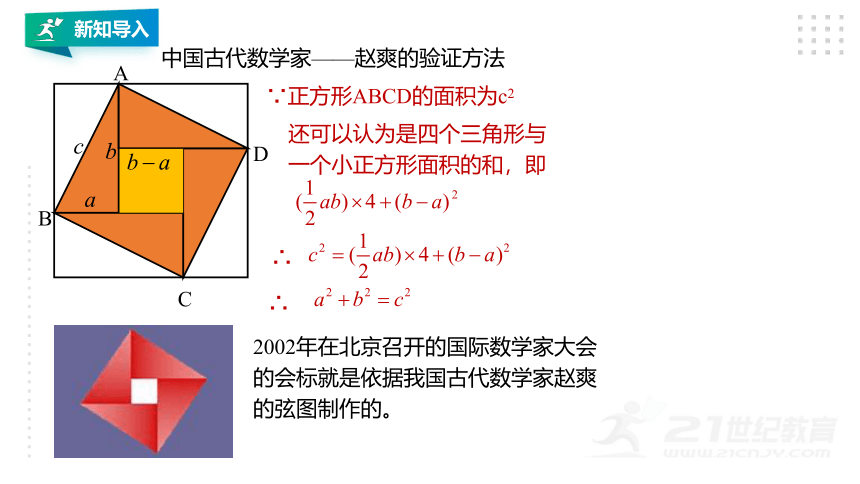
中国古代数学家——赵爽的验证方法
A
B
C
D
还可以认为是四个三角形与一个小正方形面积的和,即
∴
2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。
∴
∵正方形ABCD的面积为c2
知识讲解
勾 股 世 界
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
动手探究
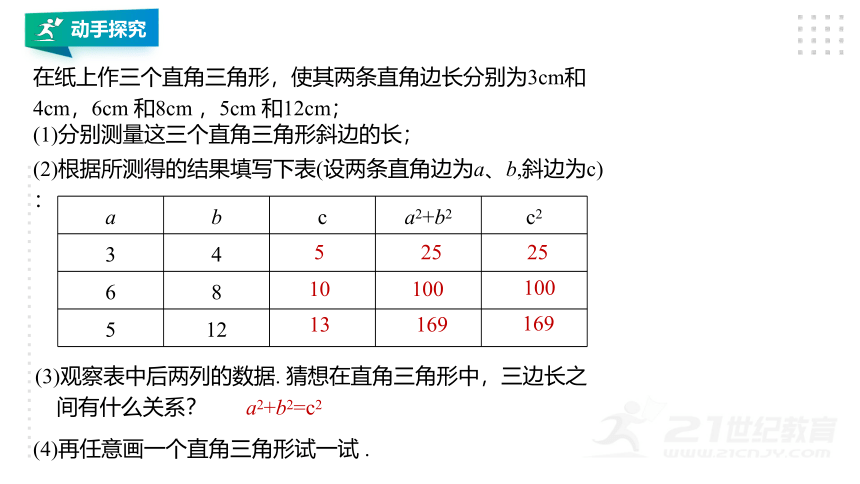
在纸上作三个直角三角形,使其两条直角边长分别为3cm和4cm,6cm 和8cm ,5cm 和12cm;
(1)分别测量这三个直角三角形斜边的长;
(2)根据所测得的结果填写下表(设两条直角边为a、b,斜边为c):
(3)观察表中后两列的数据. 猜想在直角三角形中,三边长之
间有什么关系?
a b c a2+b2 c2
3 4
6 8
5 12
5
10
13
25
100
169
25
169
100
(4)再任意画一个直角三角形试一试 .
a2+b2=c2
动手探究
a
b
a
b
a
b
a
b
c
c
c
c
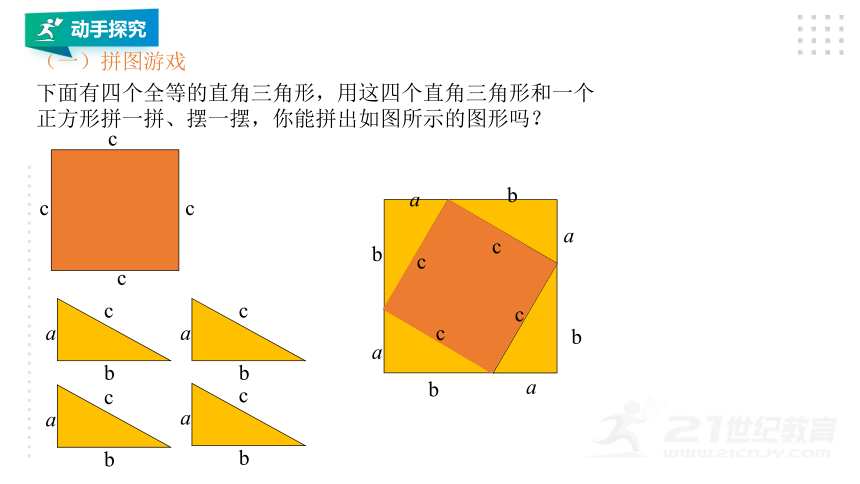
下面有四个全等的直角三角形,用这四个直角三角形和一个正方形拼一拼、摆一摆,你能拼出如图所示的图形吗?
(一)拼图游戏
a
b
c
a
b
c
a
b
c
a
b
c
c
c
c
c
知识讲解
(1) 四个直角三角形和中间一个正方
形的面积和表示为: ;
(二)填一填
(2) 大正方形的面积表示为: .
(3) 因此,我们可以得到等式: .
(4) 化简该等式的结果为: .
(5) 这个等式对于直角三角形说明了什么:
.
直角三角形两条直角边的平方和等于斜边的平方
a
b
a
b
a
b
a
b
c
c
c
c
合作学习
a
b
c
c
a
即a2+b2=c2
a
b
c
4个
a-b
a-b
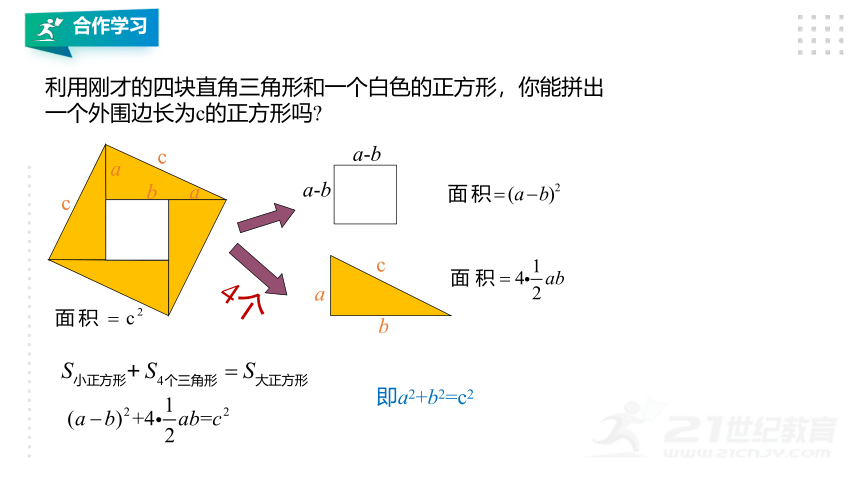
利用刚才的四块直角三角形和一个白色的正方形,你能拼出一个外围边长为c的正方形吗
知识讲解
如果a、b为直角三角形的两条直角边长, c为斜边长,那么
a
b
c
即直角三角形两直角边的平方和等于斜边的平方。
例题讲解
例1 已知△ABC中, ∠C=Rt∠ , BC=a , AC=b , AB=C
(1)已知: a=1 , b=2 , 求c;
(2)已知: a=15 , c=17 , 求b .
解: (1)根据勾股定理得:
c2=a2+b2=12 +22 =5
∵c>0, ∴c=
(2)根据勾股定理得:
b2 = c2 -a2=172 -152
=(17+15)(17-15) =64
∵b>0 , ∴b=8
a
b
c
A
B
C
已知△ABC中 , ∠C=Rt∠ , BC=a , AC=b , AB=c
若c=34 , a:b=8:15 , 求a , b.
解:设a=8x,则b=15x(x>0)
∵a2+b2=c2
∴(8x)2+(15x)2=342
∴x2=4
∵x>0, ∴x=2
∴ a=16,b=30
A
C
B
a
b
c
温馨提示:学会用方程来解决几何问题
当堂练习
解: 过A作铅垂线,过B作水平线,
两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90°
∴ AB2=AC2+BC2 =502+1202
=16900(mm2)
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
例2 如图:是一个长方形零件图,根据所给的尺寸,求两孔中心
A、B之间的距离 .
A
B
C
40
90
160
40
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题
例题讲解
“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐. 已知红莲移动的水平距离是5米,问这里的水深是多少呢?
解:设水深x米,则红莲长(x+1)米,
则 x2+52=(x+1)2
解得 x=12 (米)
答:这里的水深是12米
x
5
x+1
1
C
A
B
当堂练习
课堂小结
勾股定理:
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即a2 + b2 = c2
符号语言:
如图:在Rt△ABC中, ∠C=90°, 则 a2+b2=c2
公式变形:
a2 = c2 - b2 c=
b2 = c2 - a2 a=
b=
小 结
勾股定理的主要用途是 : 在直角三角形中,
1. 已知任意两边求第三边的长;
2. 已知一边及另两边的关系,
求另两边.
c
a
b
B
A
C
勾
弦
股
课堂练习
1. 填空
(1)a=3, b=4,则c= .
(2)c =17,a=8,则b= .
(3)c=61,b=60,则a= .
(4)a:b=3:4,c=10则a= ,b= .
c
a
b
B
A
C
5
15
11
6
8
课堂练习
A
B
C
D
7cm
2. 如图,所有的四边形都是正方形,所有的三角形都是直
角三角形,其中最大的正方形的边长为7cm,则正方形
A,B,C,D的面积之和为 cm2。
49
课堂练习
3.下图中的三角形是直角三角形,其余是正方形,求下列图
中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
课堂练习
8
x
17
16
20
x
12
5
x
方法小结: 可用勾股定理建立方程.
由勾股定理得:
82+x2=172
∴x2=172-82=225
又∵x>0
∴x=15
由勾股定理得:
x2+162=202
∴x2=202-162 =144
又∵x>0
∴x=12
由勾股定理得:
52+122=x2
∴x2=52+122=169
又∵x>0
∴x=13
4.
课堂练习
A
B
3m
1m
C
5. 有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,
此时梯脚B与墙脚C的距离是1米 . 求墙的高度 (精确到
0.1米)
解:∵∠ACB=90° , AB=3,BC=1
∴ AB2=AC2+BC2
答:墙的高度为2.8米
课堂练习
6.如图,AB∥CD,E是AD的中点, CE=EF.
求证:CF⊥AB.
解:如图,延长CE交BA的延长线于点G.
∵CD∥AB,
∴∠DCE=∠G,∠D=∠EAG.
又∵DE=AE,
∴△CDE≌△GAE(AAS).
∴CE=GE= CG.
∵CE=EF,∴EF= CG,
∴△CFG是直角三角形,且CG是斜边,∴CF⊥AB.
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
2.7.1直角三角形
浙教版 八年级上
新知导入
2002年国际数学家大会会标
思考:
1. 中间小正方形的边长和面积分别是多少?
2. 大正方形的面积可以看成哪几个图形面积相加得到?
3. 根据上题可以写出怎样一个关系式?
新知导入
中国古代数学家——赵爽的验证方法
A
B
C
D
还可以认为是四个三角形与一个小正方形面积的和,即
∴
2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。
∴
∵正方形ABCD的面积为c2
知识讲解
勾 股 世 界
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
动手探究
在纸上作三个直角三角形,使其两条直角边长分别为3cm和4cm,6cm 和8cm ,5cm 和12cm;
(1)分别测量这三个直角三角形斜边的长;
(2)根据所测得的结果填写下表(设两条直角边为a、b,斜边为c):
(3)观察表中后两列的数据. 猜想在直角三角形中,三边长之
间有什么关系?
a b c a2+b2 c2
3 4
6 8
5 12
5
10
13
25
100
169
25
169
100
(4)再任意画一个直角三角形试一试 .
a2+b2=c2
动手探究
a
b
a
b
a
b
a
b
c
c
c
c
下面有四个全等的直角三角形,用这四个直角三角形和一个正方形拼一拼、摆一摆,你能拼出如图所示的图形吗?
(一)拼图游戏
a
b
c
a
b
c
a
b
c
a
b
c
c
c
c
c
知识讲解
(1) 四个直角三角形和中间一个正方
形的面积和表示为: ;
(二)填一填
(2) 大正方形的面积表示为: .
(3) 因此,我们可以得到等式: .
(4) 化简该等式的结果为: .
(5) 这个等式对于直角三角形说明了什么:
.
直角三角形两条直角边的平方和等于斜边的平方
a
b
a
b
a
b
a
b
c
c
c
c
合作学习
a
b
c
c
a
即a2+b2=c2
a
b
c
4个
a-b
a-b
利用刚才的四块直角三角形和一个白色的正方形,你能拼出一个外围边长为c的正方形吗
知识讲解
如果a、b为直角三角形的两条直角边长, c为斜边长,那么
a
b
c
即直角三角形两直角边的平方和等于斜边的平方。
例题讲解
例1 已知△ABC中, ∠C=Rt∠ , BC=a , AC=b , AB=C
(1)已知: a=1 , b=2 , 求c;
(2)已知: a=15 , c=17 , 求b .
解: (1)根据勾股定理得:
c2=a2+b2=12 +22 =5
∵c>0, ∴c=
(2)根据勾股定理得:
b2 = c2 -a2=172 -152
=(17+15)(17-15) =64
∵b>0 , ∴b=8
a
b
c
A
B
C
已知△ABC中 , ∠C=Rt∠ , BC=a , AC=b , AB=c
若c=34 , a:b=8:15 , 求a , b.
解:设a=8x,则b=15x(x>0)
∵a2+b2=c2
∴(8x)2+(15x)2=342
∴x2=4
∵x>0, ∴x=2
∴ a=16,b=30
A
C
B
a
b
c
温馨提示:学会用方程来解决几何问题
当堂练习
解: 过A作铅垂线,过B作水平线,
两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90°
∴ AB2=AC2+BC2 =502+1202
=16900(mm2)
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
例2 如图:是一个长方形零件图,根据所给的尺寸,求两孔中心
A、B之间的距离 .
A
B
C
40
90
160
40
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题
例题讲解
“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐. 已知红莲移动的水平距离是5米,问这里的水深是多少呢?
解:设水深x米,则红莲长(x+1)米,
则 x2+52=(x+1)2
解得 x=12 (米)
答:这里的水深是12米
x
5
x+1
1
C
A
B
当堂练习
课堂小结
勾股定理:
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即a2 + b2 = c2
符号语言:
如图:在Rt△ABC中, ∠C=90°, 则 a2+b2=c2
公式变形:
a2 = c2 - b2 c=
b2 = c2 - a2 a=
b=
小 结
勾股定理的主要用途是 : 在直角三角形中,
1. 已知任意两边求第三边的长;
2. 已知一边及另两边的关系,
求另两边.
c
a
b
B
A
C
勾
弦
股
课堂练习
1. 填空
(1)a=3, b=4,则c= .
(2)c =17,a=8,则b= .
(3)c=61,b=60,则a= .
(4)a:b=3:4,c=10则a= ,b= .
c
a
b
B
A
C
5
15
11
6
8
课堂练习
A
B
C
D
7cm
2. 如图,所有的四边形都是正方形,所有的三角形都是直
角三角形,其中最大的正方形的边长为7cm,则正方形
A,B,C,D的面积之和为 cm2。
49
课堂练习
3.下图中的三角形是直角三角形,其余是正方形,求下列图
中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
课堂练习
8
x
17
16
20
x
12
5
x
方法小结: 可用勾股定理建立方程.
由勾股定理得:
82+x2=172
∴x2=172-82=225
又∵x>0
∴x=15
由勾股定理得:
x2+162=202
∴x2=202-162 =144
又∵x>0
∴x=12
由勾股定理得:
52+122=x2
∴x2=52+122=169
又∵x>0
∴x=13
4.
课堂练习
A
B
3m
1m
C
5. 有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,
此时梯脚B与墙脚C的距离是1米 . 求墙的高度 (精确到
0.1米)
解:∵∠ACB=90° , AB=3,BC=1
∴ AB2=AC2+BC2
答:墙的高度为2.8米
课堂练习
6.如图,AB∥CD,E是AD的中点, CE=EF.
求证:CF⊥AB.
解:如图,延长CE交BA的延长线于点G.
∵CD∥AB,
∴∠DCE=∠G,∠D=∠EAG.
又∵DE=AE,
∴△CDE≌△GAE(AAS).
∴CE=GE= CG.
∵CE=EF,∴EF= CG,
∴△CFG是直角三角形,且CG是斜边,∴CF⊥AB.
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
