3.2实数 课件（共20张PPT）

(共20张PPT)
3.2实数
浙教版 七年级上
新知导入
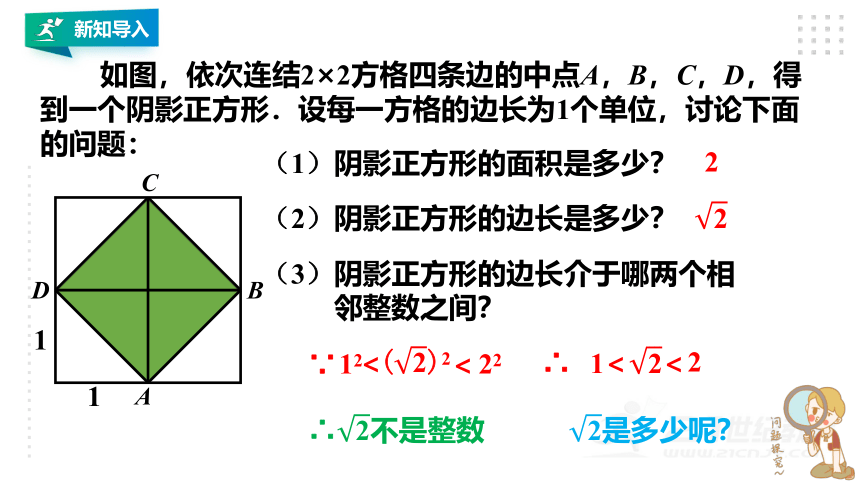
如图，依次连结2×2方格四条边的中点A，B，C，D，得到一个阴影正方形．设每一方格的边长为1个单位，讨论下面的问题：
A
B
C
D
（1）阴影正方形的面积是多少？
1
1
（2）阴影正方形的边长是多少？
（3）阴影正方形的边长介于哪两个相
邻整数之间？
2
()2
＜
12
＜
22
∵
∴
＜
1
＜
2
∴不是整数
是多少呢？
新知导入
探究1：的十分位是多少？
∵1.42＝1.96， 1.52＝2.25
∴1.4＜＜1.5
十分位取相邻两个整数
＝1.4…
探究2：的百分位是多少？
∵1.412＝1.9881， 1.422＝2.0164
∴1.41＜＜1.42
百分位取相邻两个整数
＝1.41…
探究……
＝1.41421 35623 73095 04880 16887 25209 69807 85696…
不是整数，不是有限小数，也不是无限循环小数．
即不是有理数！！！！！！
新知讲解
无理数
像这种无限不循环小数叫做无理数.
常见的无理数有三种：
（1）开不尽方的数，
（2）含π的数，
2π，3π，π＋1．
（3）有规律但无限不循环的小数，
1.010010001…（两个1之间多一个“0”）
新知讲解
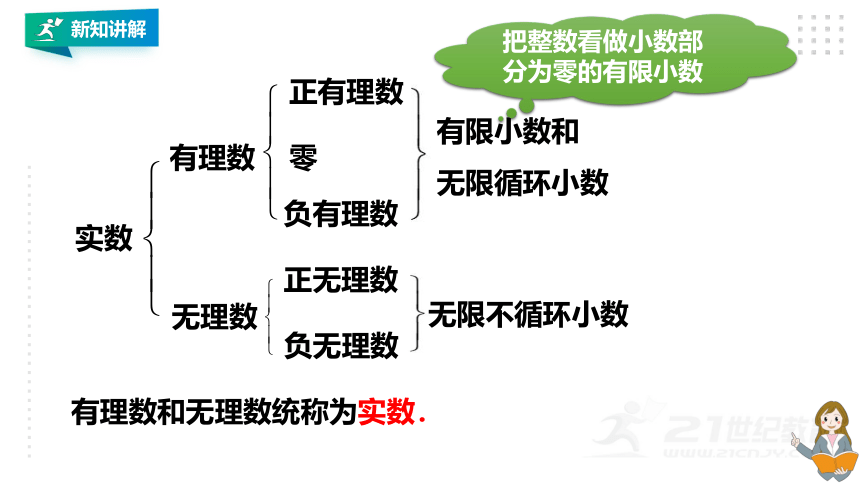
正有理数
负有理数
零
有理数
正无理数
负无理数
无理数
有限小数和
无限循环小数
把整数看做小数部分为零的有限小数
无限不循环小数
实数
有理数和无理数统称为实数．
课堂练习
1．下列各数中，哪些是有理数？哪些是无理数？
3.14159， ，0.36，，2π，，
. .
有理数：
无理数：
3.14159

0.36
. .

2π
课堂练习
2．辨一辨
（1）无理数都是无限不循环小数．
（2）无理数都是无限小数．
（3）无限小数都是无理数．
（4）带根号的数都是无理数．
（5）无理数一定都带根号．
( )
( )
( )
( )
( )
√
√
×
×
×
课堂练习
3．想一想
（1）3的相反数是______．
（3）|3|＝______．
（5）绝对值是3的数是______．
（2） 的相反数是______．
（4）| |＝______．
（6）绝对值是的数是______．
3
3
3或3
或
小结：把数从有理数扩充到实数以后，有理数中的相反数和绝对值的概念同样适用于．
问题探究
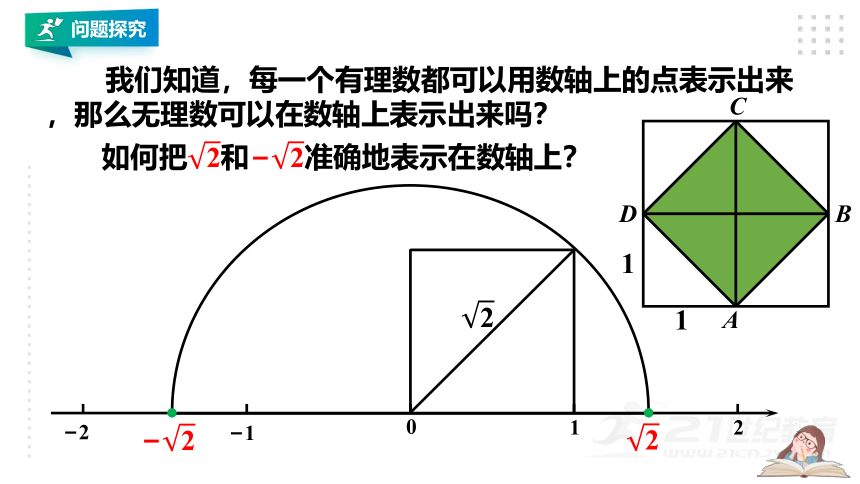
我们知道，每一个有理数都可以用数轴上的点表示出来，那么无理数可以在数轴上表示出来吗？
如何把和准确地表示在数轴上？
0
1
2
2
1
A
B
C
D
1
1
新知讲解
在实数范围内，每一个实数都可以用数轴上的点来表示；反过来，数轴上的每一个点都表示一个实数．
即：实数和数轴上的点一一对应．
例题讲解
例 把下列实数表示在数轴上，并比较它们的大小（用“＜”连接）
0
1
2
3
4
1
2
3
4
5
5
π
1.5
≈2.7
≈3.1
≈1.7
π
1.5
∴π＜＜1.5＜
小结：有理数的大小比较法则也适用于实数．
在数轴上表示的两个实数，右边的数总比左边的数大．
课堂练习
4．在哪两个相邻整数之间？在数轴上离哪一个整数更近？
()2
＜
62
＜
72
∵
∴
＜
6
＜
7
∵
()2
62
＜
72
()2
∴
在数轴上离6更近
拓展提升
已知|2020a|＋＝a，求a20202的值．
解：
由，
∴ 2020a
得 a≥2021．
＜0，
∴ |2020a|＝
2020
2020＋＝a
＝2020
＝20202
20202＝
课堂总结
正有理数
负有理数
零
有理数
正有理数
负有理数
无理数
有限小数和
无限循环小数
把整数看做小数部分为零的有限小数
无限不循环小数
实数
有理数和无理数统称为实数．
实数和数轴上的点一一对应．
正有理数
负有理数
零
有理数
正无理数
负无理数
无理数
有限小数和
无限循环小数
把整数看做小数部分为零的有限小数
无限不循环小数
实数
有理数和无理数统称为实数．
实数和数轴上的点一一对应．
板书设计
作业布置
1．作业本2 3.2实数
2．自主练习
知识补充
手算开平方—连分数法
求
S＝a2＋b（a2＞ b）
＞
＝a＋
0层：＝a
1层：＝a＋
2层：＝a＋
3层：＝a＋
…
例 求
令5＝22＋1，
则a＝2，b＝1
3层： ＝2＋
≈2.236
2层： ＝2＋
≈2.235
知识补充
第一次数学危机
https://www.21cnjy.com/help/help_extract.php