3.4圆心角选择题专题训练-2021-2022学年浙教版九年级数学上册(word版含答案)
文档属性
| 名称 | 3.4圆心角选择题专题训练-2021-2022学年浙教版九年级数学上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 440.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 00:00:00 | ||
图片预览

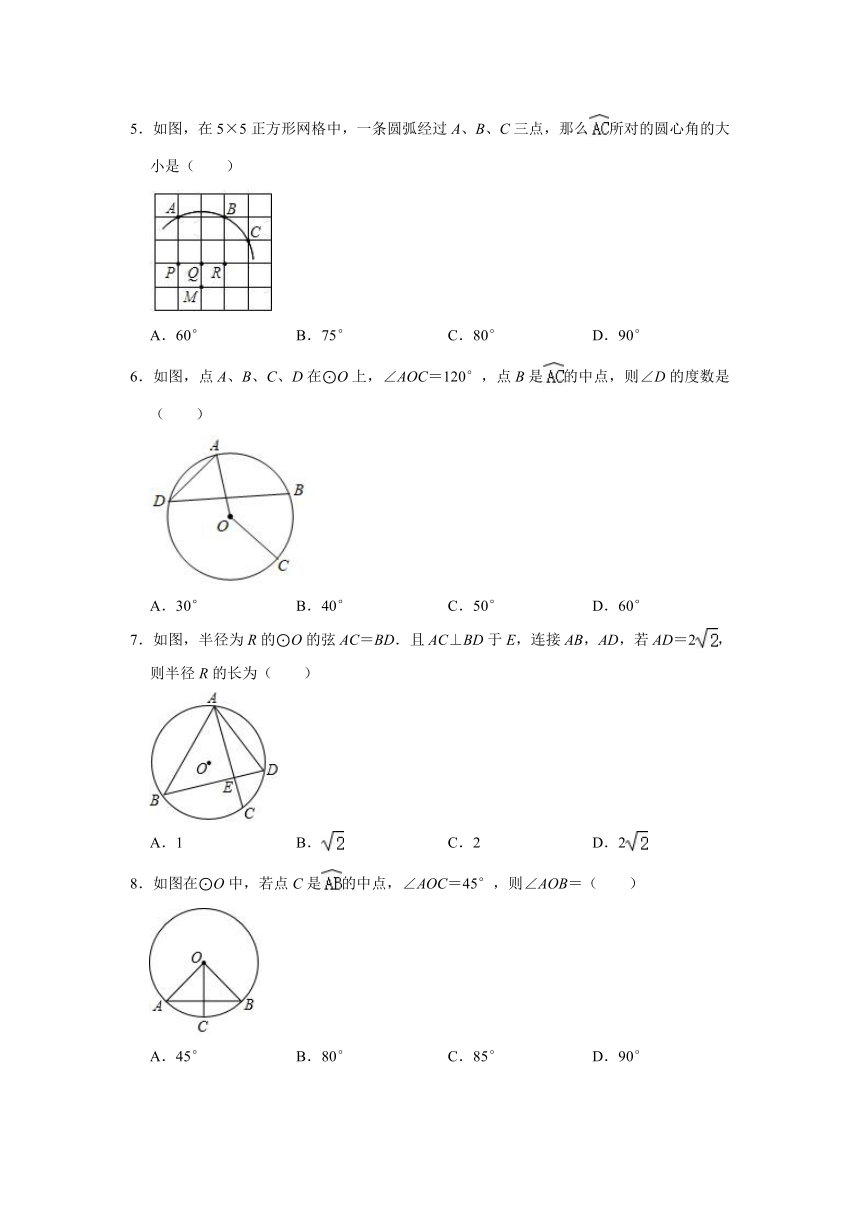



文档简介
2021-2022学年浙教版九年级数学上册《3.4圆心角》选择题专题训练(附答案)
1.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为( )
A.60° B.45° C.30° D.22.5°
2.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是( )
A.= B.= C.= D.不能确定
3.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54° B.55° C.56° D.57°
4.如图,AB是⊙O的直径,点C、D是⊙O上的点,若∠CAB=25°,则∠ADC的度数为( )
A.65° B.55° C.60° D.75°
5.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么所对的圆心角的大小是( )
A.60° B.75° C.80° D.90°
6.如图,点A、B、C、D在⊙O上,∠AOC=120°,点B是的中点,则∠D的度数是( )
A.30° B.40° C.50° D.60°
7.如图,半径为R的⊙O的弦AC=BD.且AC⊥BD于E,连接AB,AD,若AD=2,则半径R的长为( )
A.1 B. C.2 D.2
8.如图在⊙O中,若点C是的中点,∠AOC=45°,则∠AOB=( )
A.45° B.80° C.85° D.90°
9.如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
A. B. C. D.
10.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
11.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
12.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
13.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
14.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
15.如图,已知MN是⊙O的直径,弦AB⊥MN,垂足为C,若∠AON=30°,AB=,则CN=( )
A. B. C. D.2
16.⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定
17.如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
18.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
19.如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为的中点,且CD∥BE,则CD的长为( )
A. B. C. D.
20.如图,AB是⊙O的直径,∠BOD=120°,点C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为( )
A. B. C. D.
21.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且> B.Q点在上,且<
C.Q点在上,且> D.Q点在上,且<
22.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
23.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
参考答案
1.解:∵正六边形ABCDEF内接于圆O
∴的度数等于360°÷6=60°
∴∠ADB=30°
故选:C.
2.解:如图,连接OC,BC,过O作OE⊥AC于D交圆O于E,
∵把半圆沿弦AC折叠,恰好经过点O,
∴OD=OE,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴OD∥BC,
∵OA=OB,
∴OD=BC,
∴BC=OE=OB=OC,
∴∠COB=60°,
∴∠AOC=120°,
∴=,
故选:A.
3.解:连接O1P,O2P,如图,
∵P在小量角器上对应的刻度为63°,
即∠O1O2P=63°,
而O1P=O1O2,
∴∠O1PO2=∠O1O2P=63°,
∴∠PO1O2=180°﹣63°﹣63°=54°,
即点P在大量角器上对应的刻度为54°(只考虑小于90°的角).
故选:A.
4.解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=25°,
∴∠ABC=90°﹣∠CAB=65°,
∴∠ADC=∠ABC=65°.
故选:A.
5.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中
,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即所对的圆心角的大小是90°,
故选:D.
6.解:连接OB,如图,
∵点B是的中点,
∴∠AOB=∠AOC=×120°=60°,
∴∠D=∠AOB=30°.
故选:A.
7.解:连接OA,OD,
∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=2,
∴R=2,
故选:C.
8.解:∵=,
∴∠AOC=∠BOC=45°,
∴∠AOB=45°+45°=90°,
故选:D.
9.解:连OA,OB,AD,DF,过A作AG⊥CF于G点,连OE交⊙O于N,连AN,如图,
∵AB=OA=OB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴弧AB的度数=60°,
又∵AB=BC=CD,
∴弧AB=弧BC=弧CD,
∴弧ABD的度数=3×60°=180°,
∴AD为⊙O的直径,∠CFA=60°,
∵AN=AF=OE=,∴AD平分NF,∴EF过O点,
∴弧FD=弧FA,
∴△FAD为等腰直角三角形,
∴∠FCA=∠FDA=45°,FA=AD=,
在Rt△AGF中,GF=AF=,AG=GF=,
在Rt△AGC中,CG=AG=,
∴S△ACF=CF AG=×(+)×=.
故选:D.
10.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
11.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
12.解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=75°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
13.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
14.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠GCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
15.解:∵MN是⊙O的直径,弦AB⊥MN,∠AON=30°,AB=,
∴OA=2AC,AB=2AC,
∴OA=AB=4=ON,
∴OC=,
∴CN=ON﹣OC=4﹣6,
故选:A.
16.解:连接BM.
∵M为的中点,
∴AM=BM,
∵AM+BM>AB,
∴AB<2AM.
故选:C.
17.解:如图.连接BC.
∵=2,
∴=,
∴AB=BC,
∴AB+BC>AC,
∴2AB>AC,
故选:C.
18.解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).
故选:D.
19.解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x=,
∴CD=KD﹣KC=2x﹣x=x=,
故选:B.
20.解:连接OC.
∵∠DOB=120°,
∴∠AOD=60°,
∵=,
∴∠DOC=∠BOC=60°,
∴=,
∴OD⊥AC,设OA=r,则OE=r=DE=1,
∴OA=2,
∴AE==,
故选:A.
21.解:连接AD,OB,OC,
∵=180°,且=,=,
∴∠BOC=∠DOC=45°,
在圆周上取一点E连接AE,CE,
∴∠E=AOC=67.5°,
∴∠ABC=112.5°<130°,
取的中点F,连接OF,
则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠ABF=∠ABO+∠OBF=45°+(180°﹣22.5°)=123.75°<130°,
∴Q点在上,且<,
故选:B.
22.解:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距相等.
故选:D.
23.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
1.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为( )
A.60° B.45° C.30° D.22.5°
2.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是( )
A.= B.= C.= D.不能确定
3.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54° B.55° C.56° D.57°
4.如图,AB是⊙O的直径,点C、D是⊙O上的点,若∠CAB=25°,则∠ADC的度数为( )
A.65° B.55° C.60° D.75°
5.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么所对的圆心角的大小是( )
A.60° B.75° C.80° D.90°
6.如图,点A、B、C、D在⊙O上,∠AOC=120°,点B是的中点,则∠D的度数是( )
A.30° B.40° C.50° D.60°
7.如图,半径为R的⊙O的弦AC=BD.且AC⊥BD于E,连接AB,AD,若AD=2,则半径R的长为( )
A.1 B. C.2 D.2
8.如图在⊙O中,若点C是的中点,∠AOC=45°,则∠AOB=( )
A.45° B.80° C.85° D.90°
9.如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
A. B. C. D.
10.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
11.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
12.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
13.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
14.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
15.如图,已知MN是⊙O的直径,弦AB⊥MN,垂足为C,若∠AON=30°,AB=,则CN=( )
A. B. C. D.2
16.⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定
17.如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
18.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
19.如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为的中点,且CD∥BE,则CD的长为( )
A. B. C. D.
20.如图,AB是⊙O的直径,∠BOD=120°,点C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为( )
A. B. C. D.
21.如图所示A、B、C、D四点在⊙O上的位置,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确?( )
A.Q点在上,且> B.Q点在上,且<
C.Q点在上,且> D.Q点在上,且<
22.如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
23.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
参考答案
1.解:∵正六边形ABCDEF内接于圆O
∴的度数等于360°÷6=60°
∴∠ADB=30°
故选:C.
2.解:如图,连接OC,BC,过O作OE⊥AC于D交圆O于E,
∵把半圆沿弦AC折叠,恰好经过点O,
∴OD=OE,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴OD∥BC,
∵OA=OB,
∴OD=BC,
∴BC=OE=OB=OC,
∴∠COB=60°,
∴∠AOC=120°,
∴=,
故选:A.
3.解:连接O1P,O2P,如图,
∵P在小量角器上对应的刻度为63°,
即∠O1O2P=63°,
而O1P=O1O2,
∴∠O1PO2=∠O1O2P=63°,
∴∠PO1O2=180°﹣63°﹣63°=54°,
即点P在大量角器上对应的刻度为54°(只考虑小于90°的角).
故选:A.
4.解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=25°,
∴∠ABC=90°﹣∠CAB=65°,
∴∠ADC=∠ABC=65°.
故选:A.
5.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中
,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即所对的圆心角的大小是90°,
故选:D.
6.解:连接OB,如图,
∵点B是的中点,
∴∠AOB=∠AOC=×120°=60°,
∴∠D=∠AOB=30°.
故选:A.
7.解:连接OA,OD,
∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=2,
∴R=2,
故选:C.
8.解:∵=,
∴∠AOC=∠BOC=45°,
∴∠AOB=45°+45°=90°,
故选:D.
9.解:连OA,OB,AD,DF,过A作AG⊥CF于G点,连OE交⊙O于N,连AN,如图,
∵AB=OA=OB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴弧AB的度数=60°,
又∵AB=BC=CD,
∴弧AB=弧BC=弧CD,
∴弧ABD的度数=3×60°=180°,
∴AD为⊙O的直径,∠CFA=60°,
∵AN=AF=OE=,∴AD平分NF,∴EF过O点,
∴弧FD=弧FA,
∴△FAD为等腰直角三角形,
∴∠FCA=∠FDA=45°,FA=AD=,
在Rt△AGF中,GF=AF=,AG=GF=,
在Rt△AGC中,CG=AG=,
∴S△ACF=CF AG=×(+)×=.
故选:D.
10.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
11.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
12.解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=75°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
13.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
14.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠GCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
15.解:∵MN是⊙O的直径,弦AB⊥MN,∠AON=30°,AB=,
∴OA=2AC,AB=2AC,
∴OA=AB=4=ON,
∴OC=,
∴CN=ON﹣OC=4﹣6,
故选:A.
16.解:连接BM.
∵M为的中点,
∴AM=BM,
∵AM+BM>AB,
∴AB<2AM.
故选:C.
17.解:如图.连接BC.
∵=2,
∴=,
∴AB=BC,
∴AB+BC>AC,
∴2AB>AC,
故选:C.
18.解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).
故选:D.
19.解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x=,
∴CD=KD﹣KC=2x﹣x=x=,
故选:B.
20.解:连接OC.
∵∠DOB=120°,
∴∠AOD=60°,
∵=,
∴∠DOC=∠BOC=60°,
∴=,
∴OD⊥AC,设OA=r,则OE=r=DE=1,
∴OA=2,
∴AE==,
故选:A.
21.解:连接AD,OB,OC,
∵=180°,且=,=,
∴∠BOC=∠DOC=45°,
在圆周上取一点E连接AE,CE,
∴∠E=AOC=67.5°,
∴∠ABC=112.5°<130°,
取的中点F,连接OF,
则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠ABF=∠ABO+∠OBF=45°+(180°﹣22.5°)=123.75°<130°,
∴Q点在上,且<,
故选:B.
22.解:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距相等.
故选:D.
23.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
同课章节目录
