2.1二次函数

(共20张PPT)
你知道篮球运动的路线是什么曲线吗？
我们现有的知识能解释这个现象吗？
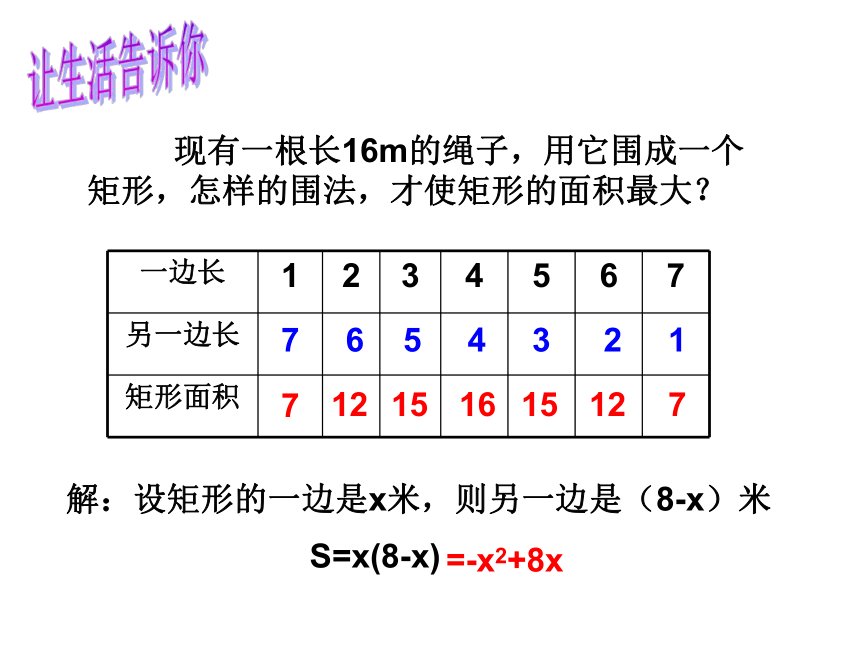
现有一根长16m的绳子，用它围成一个矩形，怎样的围法，才使矩形的面积最大？
解：设矩形的一边是x米，则另一边是（8-x）米
S=x(8-x)
一边长 1 2 3 4 5 6 7
另一边长
矩形面积
7
6
5
4
3
2
1
7
12
15
16
15
12
7
=-x2+8x
请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系：
(1)圆的面积 y ( cm2 )与圆的半径 x ( cm )
y =πx2
(2)某商店1月份的利润是2万元，2、3月份利润逐月增长，这两个月利润的月平均增长率为x，3月份的利润为y(万元)
y = 2(1+x)2
课本26页，完成合作学习
(3)拟建中的一个温室的平面图如图,如果温室外围是一个矩形，周长为120m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2)。
1
1
1
3
x
y = (60-x-4)(x-2)
1.y =πx2
2.y = 2(1+x)2
3.y= (60-x-4)(x-2)
=2x2+4x+2
=-x2+58x-112
上述三个问题中的函数解析式具有哪些共同的特征
经化简后都具有y=ax +bx+c 的形式.
(a,b,c是常数, )
且a≠0
我们把形如y=ax +bx+c(其中a,b,c是常数，a≠0 )的函数叫做二次函数
其中，ax 称为二次项，a称为二次项系数；
bx称为一次项，b称为一次项系数；
C称为常数项。
二次函数的一般式
下列函数中,哪些是二次函数
先化简后判断
不是，是一次函数
不是，右边是分式不是整式
是二次函数
=v2-1
是二次函数
=3n2-3n
是二次函数
=2t+1
不是，是一次函数
判断一个函数是否是二次函数，需要满足几个特征？
填表：写出下列二次函数的二次项系数、一次 项系数和常数项。
函数解析式 二次项
系数 一次项系数 常数项
y=2x2-x-1
m=-3n(n+2)
S=3(t+1)(t-2)
2
-1
-1
-3
-6
0
=3t2-3t-6
3
-3
-6
先化简成一般式
例1：函数
（1）m取什么值时，此函数是正比例函数？
（2）m取什么值时，此函数是反比例函数？
（3）m取什么值时，此函数是二次函数？
解：
由 ，得
由 ，得
由 ，得
例2：已知二次函数y=x2+px+q，当x=1时， y=4；当x=2时y=-5，求二次函数解析式。
解：把x=1，y=4;x=2,y=-5代入，得
解得
∴二次函数解析式是y=x2-12x+15
变式：已知函数y=ax2+bx+c(a≠0),当x=0时，y=-5；当x=1时，y=-8；当x=-1时，y=0，求函数解析式。
解：依题意，得
解得
∴二次函数解析式是y=x2-4x-5
1、若函数 是二次函数，求m的值。
2、已知函数y=ax2+bx+3，当x=2时，函数值是3； 当x=-2时，函数值是2.求函数解析式。
由 ，得
例3: 如图，一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形 (图中阴影部分 ) ，设AE=BF=CG=DH=x(cm)，四边形 EFGH的面积为y(cm2)，求 : 　
(l)求y关于 x的函数解析式和自变量x的取值范围
(2)当x分别为0.25，0.5，1，1.5，
1.75 时 ，求对应的四边形EFGH的
面积y，并列表表示.
x 0.25 0.5 1 1.5 1.75
y 2
A
E
B
H
D
F
C
G
3.125
2.5
2.5
3.125
y=2x2-4x+4 (0自变量要有实际意义
通过本堂课的学习
驶向成功的彼岸
我认识到
……
我体会到
……
认识到：
1、二次函数的概念；
2、用待定系数法求二次函数的解析式；
3、用二次函数表示实际问题中的数量关系，并求自变量取值范围。
体会到：
二次函数在生活中有着广泛的
应用，函数与方程密切相关
1、作业本（1）
2、课后作业《教与学》
如图，已知矩形ABCD中，AB=6cm，BC=8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B沿BC向点C以2cm/s速度移动，P、Q分别从A、B同时出发，有一点到达终点即停止运动，设移动时间为t（s）。
C
A
B
D
P
Q
（1）求S△PQB与t的函数关系式，并写出t的取值范围。
（2）t为何值时，△PQB的面积为8cm2
(3)拟建中的一个温室的平面图如图,如果温室外围是一个矩形，周长为120m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2)。
1
1
1
3
x
y = (60-x-4)(x-2)
由 ， 得
2根据实际问题中的量及相关量有实际意义
=-x2+58x-112