3.1圆（1）

(共18张PPT)
想一想：
现在学校要求你在操场中间作一个半径5m的圆，请你说说有什么方法作这个圆？
如果现在只提供粉笔和绳子这两样工具，那这个圆该怎么作呢？
线段OP绕它固定的一个端点O旋转一周，另一端点P所经过的封闭曲线叫做圆。
封闭曲
线
定点O叫做圆心。
线段OP叫做圆的半径。
表示：
以O为圆心的圆，记做⊙O”，
读做“圆O”。
在同一平面内，
圆上任意两点间的部分，简称弧.
直径将圆分成两部分，每一部分都称为半圆.
连接圆上任意两点间的线段
经过圆心的弦
小于半圆的弧
大于半圆的弧
弦：
直径：
圆弧：
半圆：
劣弧：
优弧：
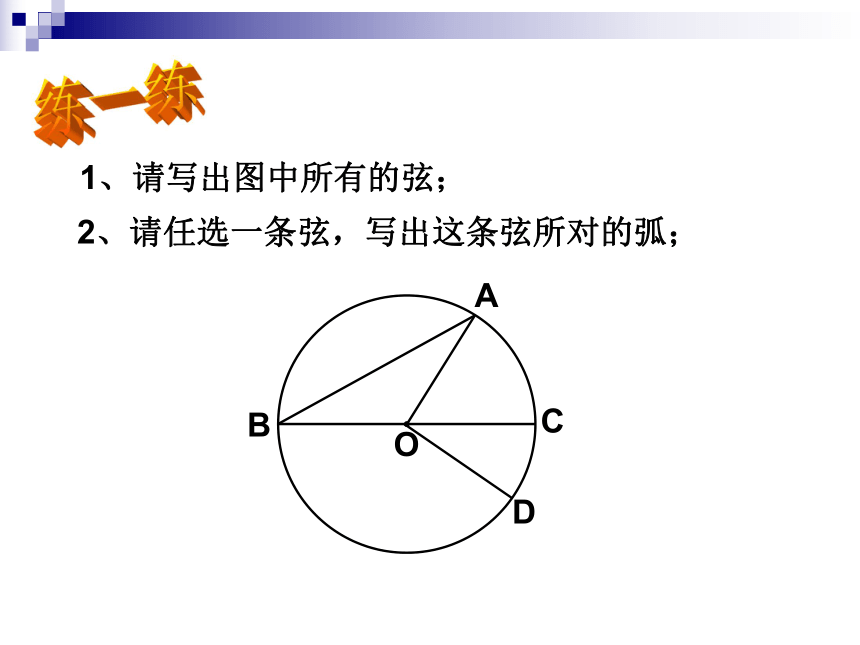
1、请写出图中所有的弦；
2、请任选一条弦，写出这条弦所对的弧；
A
B
C
O
D
2、下列命题中，哪些是真命题？哪些是假命题？
(1)弦是直径；
(2)圆上的任意两点都能将圆分成一条劣弧和一条优弧；
(3)半径相等的圆一定能重合；
假命题
假命题
真命题
O1
r
O2
r
等圆
同心圆
圆心相同，半径不同
半径相同，圆心不同
确定一个圆的要素:
圆心确定其位置，
一是圆心，
二是半径．
半径确定其大小．
在一次军事训练大比拼中，甲乙丙三位教官进行射击比赛，规定谁射击的落点离中心O越近谁就获胜。如右图中A、B、C三点分别是他们三人的第一次射击落点，你认为这一轮中谁的成绩最好？
观察右图，说说A、B、C三点和⊙O之间的位置关系？
如图，设⊙O的半径为r，点到圆心的距离为d。
点与圆的位置关系
如图，设⊙O的半径为r，A点在圆上，B点在圆内，
C点在圆外，那么
若点A在⊙O上
若点B在⊙O内
若点C在⊙O外
OA＝r ， OB ＜ r， OC＞r．
即
点的位置可以确定该点到圆心的距离与半径的关系，反过来，已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系。
1、已知⊙O的面积为25π，判断点P与⊙O的
位置关系．
（1）若PO=5.5，则点P在 ；
（2）若PO=4，则点P在 ；
（3）若PO= ，则点P在圆上．
圆外
圆内
5
2、在直角三角形ABC中，∠C=90o，
AC=3cm ， AB=5cm。若以点C为
圆心，画一个半径为3cm的圆，
试判断点A、点B和⊙C 的相互位
置关系。
C
A
B
例1:如图所示，在A地正北60m的Ｂ处有一幢民房，正西80m的C处有一变电设施，在BC的中点D处是一古建筑。因施工需要，必须在A处进行一次爆破。
(1)为使民房、变电设施、古建筑都不遭到破坏，问爆破影响面的半径应控制在什么范围内？
例1:如图所示，在A地正北60m的Ｂ处有一幢民房，正西80m的C处有一变电设施，在BC的中点D处是一古建筑。因施工需要，必须在A处进行一次爆破。
（2）现在在AB两地之间是一条高速公路，为了使爆炸不影响到交通安全，这个时候爆炸应该问爆破影响面的半径应控制在什么范围内？
例1:如图所示，在A地正北60m的Ｂ处有一幢民房，正西80m的C处有一变电设施，在BC的中点D处是一古建筑。
（3）现在A地有一气象站检测到台风中心将从C点向B点移动，距台风中心50m范围内为受影响区域。问A处是否会受到这次台风影响？
能让大家与你一起分享这节课的收获和体验吗？
1、课本第60页作业题A组：
1、 2、 3、 4。
2、作业本3.1(1)