2021-2022学年浙教新版七年级上册数学《第6章 图形的初步知识》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教新版七年级上册数学《第6章 图形的初步知识》单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 14:24:39 | ||
图片预览




文档简介
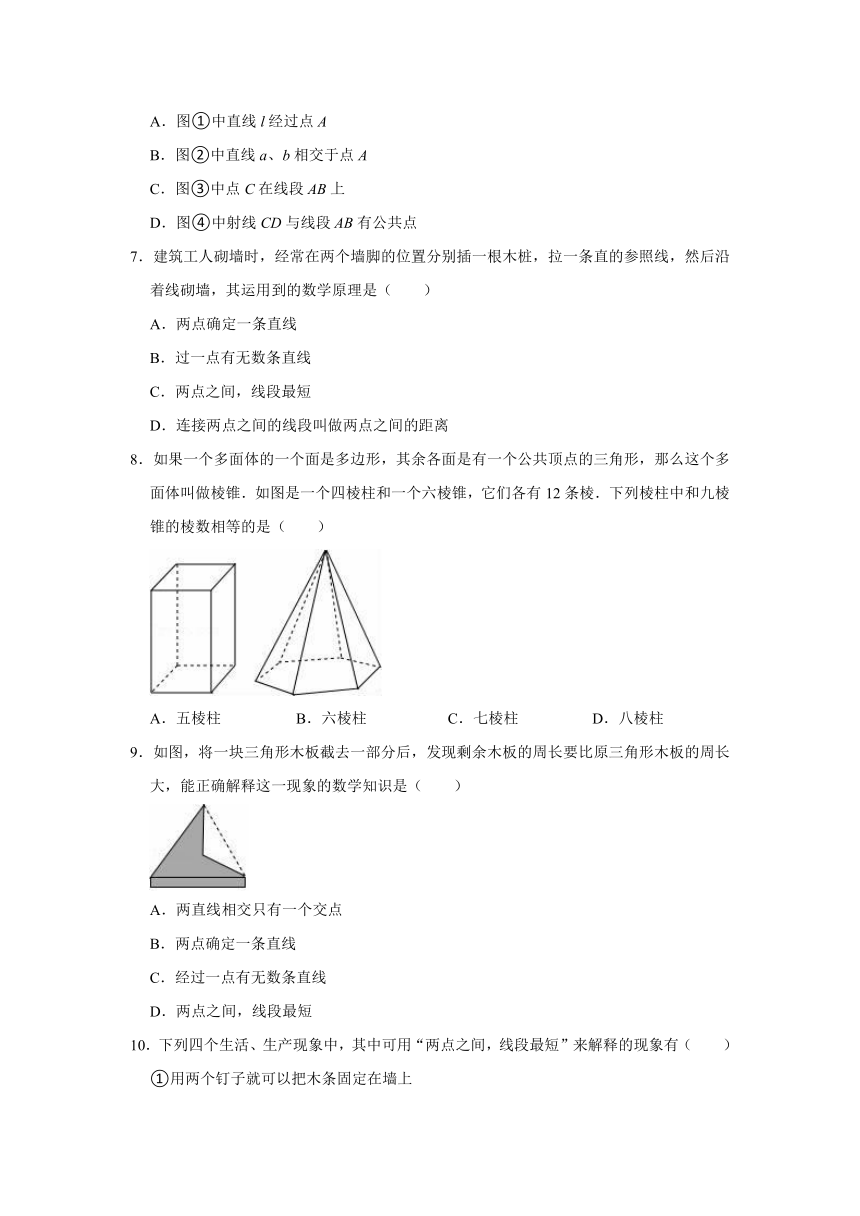
2021-2022学年浙教新版七年级上册数学《第6章 图形的初步知识》单元测试卷
一.选择题
1.下列几何体,都是由平面围成的是( )
A.圆柱 B.三棱柱 C.圆锥 D.球
2.下面几何体中,表面都是平的是( )
A.圆柱 B.圆锥 C.棱柱 D.球
3.下面的图形,是由A、B、C、D中的哪个图旋转形成的( )
A. B. C. D.
4.在下列图形中,是平面上曲线图形的有( )个
①三角形②正方形③长方形④圆.
A.1 B.2 C.3 D.4
5.如图,下列语句错误的是( )
A.直线AC和BD是不同的直线
B.AD=AB+BC+CD
C.射线DC和DB是同一条射线
D.射线BA和BD不是同一条射线
6.下列说法错误的是( )
A.图①中直线l经过点A
B.图②中直线a、b相交于点A
C.图③中点C在线段AB上
D.图④中射线CD与线段AB有公共点
7.建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,拉一条直的参照线,然后沿着线砌墙,其运用到的数学原理是( )
A.两点确定一条直线
B.过一点有无数条直线
C.两点之间,线段最短
D.连接两点之间的线段叫做两点之间的距离
8.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
9.如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( )
A.两直线相交只有一个交点
B.两点确定一条直线
C.经过一点有无数条直线
D.两点之间,线段最短
10.下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有( )
①用两个钉子就可以把木条固定在墙上
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
③从A地到B地架设电线,总是尽可能沿着直线架设
④把弯曲的公路改直,就能缩短路程.
A.①② B.①③ C.②④ D.③④
二.填空题
11.六棱柱有 个顶点, 个面, 条棱.
12.长方体是由 个面围成,圆柱是由 个面围成,圆锥是由 个面围成.
13.把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是 .
14.圆锥由 个面围成,其中 个平面, 个曲面.
15.如图,在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,甲同学认为是两点确定一条直线,乙同学认为是两点之间线段最短.你认为 同学的说法是正确的.
16.如图,图中共有 个梯形.
17.如图,平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为 .
18.直线上有2010个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有 个点.
19.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
20.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 cm3.
三.解答题
21.用彩带捆扎一个圆柱形的蛋糕盒(如图,打结处正好是底面圆心,打结用去彩带18cm.
(1)扎这个盒子至少用去彩带多少厘米?
(2)这个蛋糕盒子的体积是多少立方厘米?
(3)蛋糕的直径比盒子直径少3cm,高比盒子矮5cm,张琳打开盒子,沿着蛋糕底面的直径垂直切开,平均分成两部分,这时蛋糕的表面积增加多少平方厘米?
22.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
23.两个圆柱体容器如图所示,它们的直径分别为4cm和8cm,高分别为39cm和10cm.把容器一倒满水,然后将容器一中的水倒入容器二中,求容器二中的水面离容器口有多少厘米,
24.如图、把一个圆分成四个扇形,求出四个扇形的圆心角(按照从大到小排序).
25.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC、BD交于E点;
(2)作射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
26.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
27.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
参考答案与试题解析
一.选择题
1.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有三棱柱是由5个平面围成的,
故选:B.
2.解:A、圆柱的侧面不是平面图形,不符合题意;
B、圆锥的侧面不是平面图形,不符合题意;
C、棱柱表面是平面图形,符合题意;
D、球表面不是平面图形,不符合题意.
故选:C.
3.解:直角梯形绕直角边旋转得圆台,故A正确;
故选:A.
4.解:∵三角形、正方形、长方形都是平面直线图形,圆是平面曲线图形,
∴平面上曲线图形只有圆,
故选:A.
5.解:A、因为直线是可以向两端无限延伸的,它可以用这条直线上的两个点来表示,所以在A中,直线AC和BD是相同的直线,故A错.
B、∵AD是三条线段的和,∴AD=AB+BC+CD,故B正确;
C、端点相同的两条射线是同一条射线,则射线DC和DB是同一条射线,故C正确;
D、端点相同的两条射线是同一条射线,所以在D中,射线BA和BD不是同一条射线,方向相反,故D正确;
故选:A.
6.解:A、图①中直线l经过点A,正确;
B、图②中直线a、b相交于点A,正确;
C、图③中点C在线段AB外,故本选项错误;
D、图④中射线CD与线段AB有公共点,正确;
故选:C.
7.解:建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,拉一条直的参照线,然后沿着线砌墙,其运用到的数学原理是:两点确定一条直线.
故选:A.
8.解:九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,
A、五棱柱共15条棱,故A错误;
B、六棱柱共18条棱,故B正确;
C、七棱柱共21条棱,故C错误;
D、八棱柱共24条棱,故D错误;
故选:B.
9.解:如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是:两点之间线段最短.
故选:D.
10.解:①用两个钉子就可以把木条固定在墙上,是两点确定一条直线,故此选项错误;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,故此选项错误;
③从A地到B地架设电线,总是尽可能沿着直线架设,是两点之间,线段最短,故此选项正确;
④把弯曲的公路改直,就能缩短路程,是两点之间,线段最短,故此选项正确;
故选:D.
二.填空题
11.解:六棱柱上下两个底面是6边形,侧面是6个长方形.所以共有12个顶点;8个面;18条棱.
故答案为12,8,18.
12.解:长方体是由上下,左右,前后共6个面组成;
圆柱是由上下两个底面,中间一个侧面共3个面组成;
圆锥是由一个底面和一个侧面共2个面组成.
故答案为6,3,2.
13.解:把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是:两点之间线段最短.
故答案为:两点之间线段最短.
14.解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
15.解:在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,应该是两点确定一条直线,而不是两点之间线段最短.
故答案为:甲.
16.解:由图形的特点可知,一个平行四边形和一个三角形可组成一个梯形,且图形中的梯形的形状、大小相同,共有10个.
故答案为10.
17.解:射线OD上的第1个数字为4,
第2个为旋转一周后,是第10个,
第3个,再旋转一周,转过了6个数字;
…
由此发现规律:每两个数字之差为6,那么射线OD上的第n个数字表示为6n﹣2.
18.解:第一次:2010+(2010﹣1)=2×2010﹣1,
第二次:2×2010﹣1+2×2010﹣1﹣1=4×2010﹣3,
第三次:4×2010﹣3+4×2010﹣3﹣1=8×2010﹣7.
∴经过3次这样的操作后,直线上共有8×2010﹣7=16073个点.
故答案为:16073.
19.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
20.解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
故它们的体积分别为16πcm3或32πcm3.
故答案为:16π或32π.
三.解答题
21.解:(1)2(30×2+20×2)+18=218cm,
答:扎这个盒子至少用去彩带218cm;
(2)由圆柱的体积,得
3.14×()2×20=14130(cm3),
答:这个蛋糕盒子的体积是14130cm3
(3)蛋糕的直径是30﹣3=27cm,蛋糕的高是20﹣5=15cm,
截面的面积是27×15×2=810cm2.
答:蛋糕的表面积增加810平方厘米.
22.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
23.解:设第二个容器的水面离容器口有xcm,
第一个容器中水的体积为π×39,
第二个容器中水的体积为π×(10﹣x);
∵水的体积不变,
∴π×22×39=π×42×(10﹣x),
解得x=0.25.
即容器二中的水面离容器口有0.25厘米.
24.解:因为一个圆周角为360°,所以分成的四个扇形的圆心角分别是:
360°×40%=144°
360°×25%=90°
360°×20%=72°
360°×15%=54°
25.解:(1)如图所示:
;
(2)如图所示,
(3)如图所示,
.
26.解:所画图形如下:
27.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
一.选择题
1.下列几何体,都是由平面围成的是( )
A.圆柱 B.三棱柱 C.圆锥 D.球
2.下面几何体中,表面都是平的是( )
A.圆柱 B.圆锥 C.棱柱 D.球
3.下面的图形,是由A、B、C、D中的哪个图旋转形成的( )
A. B. C. D.
4.在下列图形中,是平面上曲线图形的有( )个
①三角形②正方形③长方形④圆.
A.1 B.2 C.3 D.4
5.如图,下列语句错误的是( )
A.直线AC和BD是不同的直线
B.AD=AB+BC+CD
C.射线DC和DB是同一条射线
D.射线BA和BD不是同一条射线
6.下列说法错误的是( )
A.图①中直线l经过点A
B.图②中直线a、b相交于点A
C.图③中点C在线段AB上
D.图④中射线CD与线段AB有公共点
7.建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,拉一条直的参照线,然后沿着线砌墙,其运用到的数学原理是( )
A.两点确定一条直线
B.过一点有无数条直线
C.两点之间,线段最短
D.连接两点之间的线段叫做两点之间的距离
8.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
9.如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( )
A.两直线相交只有一个交点
B.两点确定一条直线
C.经过一点有无数条直线
D.两点之间,线段最短
10.下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有( )
①用两个钉子就可以把木条固定在墙上
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
③从A地到B地架设电线,总是尽可能沿着直线架设
④把弯曲的公路改直,就能缩短路程.
A.①② B.①③ C.②④ D.③④
二.填空题
11.六棱柱有 个顶点, 个面, 条棱.
12.长方体是由 个面围成,圆柱是由 个面围成,圆锥是由 个面围成.
13.把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是 .
14.圆锥由 个面围成,其中 个平面, 个曲面.
15.如图,在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,甲同学认为是两点确定一条直线,乙同学认为是两点之间线段最短.你认为 同学的说法是正确的.
16.如图,图中共有 个梯形.
17.如图,平面内有公共端点的六条射线:OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字:1,2,3,4,5,6,7,….根据规律将射线OD上的第n个数字(从O向D数)用含正整数n的式子表示为 .
18.直线上有2010个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有 个点.
19.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
20.将一个长4cm宽2cm的长方形绕它的一边所在的直线旋转一周,所得几何体的体积为 cm3.
三.解答题
21.用彩带捆扎一个圆柱形的蛋糕盒(如图,打结处正好是底面圆心,打结用去彩带18cm.
(1)扎这个盒子至少用去彩带多少厘米?
(2)这个蛋糕盒子的体积是多少立方厘米?
(3)蛋糕的直径比盒子直径少3cm,高比盒子矮5cm,张琳打开盒子,沿着蛋糕底面的直径垂直切开,平均分成两部分,这时蛋糕的表面积增加多少平方厘米?
22.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
23.两个圆柱体容器如图所示,它们的直径分别为4cm和8cm,高分别为39cm和10cm.把容器一倒满水,然后将容器一中的水倒入容器二中,求容器二中的水面离容器口有多少厘米,
24.如图、把一个圆分成四个扇形,求出四个扇形的圆心角(按照从大到小排序).
25.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC、BD交于E点;
(2)作射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
26.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
27.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
参考答案与试题解析
一.选择题
1.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有三棱柱是由5个平面围成的,
故选:B.
2.解:A、圆柱的侧面不是平面图形,不符合题意;
B、圆锥的侧面不是平面图形,不符合题意;
C、棱柱表面是平面图形,符合题意;
D、球表面不是平面图形,不符合题意.
故选:C.
3.解:直角梯形绕直角边旋转得圆台,故A正确;
故选:A.
4.解:∵三角形、正方形、长方形都是平面直线图形,圆是平面曲线图形,
∴平面上曲线图形只有圆,
故选:A.
5.解:A、因为直线是可以向两端无限延伸的,它可以用这条直线上的两个点来表示,所以在A中,直线AC和BD是相同的直线,故A错.
B、∵AD是三条线段的和,∴AD=AB+BC+CD,故B正确;
C、端点相同的两条射线是同一条射线,则射线DC和DB是同一条射线,故C正确;
D、端点相同的两条射线是同一条射线,所以在D中,射线BA和BD不是同一条射线,方向相反,故D正确;
故选:A.
6.解:A、图①中直线l经过点A,正确;
B、图②中直线a、b相交于点A,正确;
C、图③中点C在线段AB外,故本选项错误;
D、图④中射线CD与线段AB有公共点,正确;
故选:C.
7.解:建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,拉一条直的参照线,然后沿着线砌墙,其运用到的数学原理是:两点确定一条直线.
故选:A.
8.解:九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,
A、五棱柱共15条棱,故A错误;
B、六棱柱共18条棱,故B正确;
C、七棱柱共21条棱,故C错误;
D、八棱柱共24条棱,故D错误;
故选:B.
9.解:如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是:两点之间线段最短.
故选:D.
10.解:①用两个钉子就可以把木条固定在墙上,是两点确定一条直线,故此选项错误;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,故此选项错误;
③从A地到B地架设电线,总是尽可能沿着直线架设,是两点之间,线段最短,故此选项正确;
④把弯曲的公路改直,就能缩短路程,是两点之间,线段最短,故此选项正确;
故选:D.
二.填空题
11.解:六棱柱上下两个底面是6边形,侧面是6个长方形.所以共有12个顶点;8个面;18条棱.
故答案为12,8,18.
12.解:长方体是由上下,左右,前后共6个面组成;
圆柱是由上下两个底面,中间一个侧面共3个面组成;
圆锥是由一个底面和一个侧面共2个面组成.
故答案为6,3,2.
13.解:把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是:两点之间线段最短.
故答案为:两点之间线段最短.
14.解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
15.解:在利用量角器画一个40°的∠AOB的过程中,对于先找点B,再画射线OB这一步骤的画图依据,应该是两点确定一条直线,而不是两点之间线段最短.
故答案为:甲.
16.解:由图形的特点可知,一个平行四边形和一个三角形可组成一个梯形,且图形中的梯形的形状、大小相同,共有10个.
故答案为10.
17.解:射线OD上的第1个数字为4,
第2个为旋转一周后,是第10个,
第3个,再旋转一周,转过了6个数字;
…
由此发现规律:每两个数字之差为6,那么射线OD上的第n个数字表示为6n﹣2.
18.解:第一次:2010+(2010﹣1)=2×2010﹣1,
第二次:2×2010﹣1+2×2010﹣1﹣1=4×2010﹣3,
第三次:4×2010﹣3+4×2010﹣3﹣1=8×2010﹣7.
∴经过3次这样的操作后,直线上共有8×2010﹣7=16073个点.
故答案为:16073.
19.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
20.解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
故它们的体积分别为16πcm3或32πcm3.
故答案为:16π或32π.
三.解答题
21.解:(1)2(30×2+20×2)+18=218cm,
答:扎这个盒子至少用去彩带218cm;
(2)由圆柱的体积,得
3.14×()2×20=14130(cm3),
答:这个蛋糕盒子的体积是14130cm3
(3)蛋糕的直径是30﹣3=27cm,蛋糕的高是20﹣5=15cm,
截面的面积是27×15×2=810cm2.
答:蛋糕的表面积增加810平方厘米.
22.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
23.解:设第二个容器的水面离容器口有xcm,
第一个容器中水的体积为π×39,
第二个容器中水的体积为π×(10﹣x);
∵水的体积不变,
∴π×22×39=π×42×(10﹣x),
解得x=0.25.
即容器二中的水面离容器口有0.25厘米.
24.解:因为一个圆周角为360°,所以分成的四个扇形的圆心角分别是:
360°×40%=144°
360°×25%=90°
360°×20%=72°
360°×15%=54°
25.解:(1)如图所示:
;
(2)如图所示,
(3)如图所示,
.
26.解:所画图形如下:
27.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
