3.4圆心角 同步练习2020-2021学年浙教版数学九年级上册(word版含答案)
文档属性
| 名称 | 3.4圆心角 同步练习2020-2021学年浙教版数学九年级上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 446.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 19:33:41 | ||
图片预览



文档简介
圆心角
一、单选题
1.在半径为的圆中,长度等于的弦所对的弧的度数为( )
A. B. C.或 D.或
2.如图,在⊙O中,,,,则的度数是( )
A. B. C. D.
3.如图所示,C是⊙O上一点,若,则∠AOB的度数为( )
A.20° B.40° C.80° D.140°
4.如图,AB是⊙O的直径,,,则=( )
A.30° B.45° C.60° D.以上都不正确
5.如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )
A.38° B.52° C.76° D.104°
6.如图所示,⊙O的弦AB、AC的夹角为50°,M、N分别是、的中点,则∠MON的度数是( )
A.100° B.110° C.120° D.130°
7.在⊙O中,C是的中点,D是上的任一点(与点A、C不重合),则( )
A.AC+CB=AD+DB B.AC+CB<AD+DB
C.AC+CB>AD+DB D.AC+CB与AD+DB的大小关系不确定
8.如图,在平行四边形ABCO中,,点A,B在⊙O上,点D在优弧ADB上,,则的度数为( )
A.165° B.155° C.145° D.135°
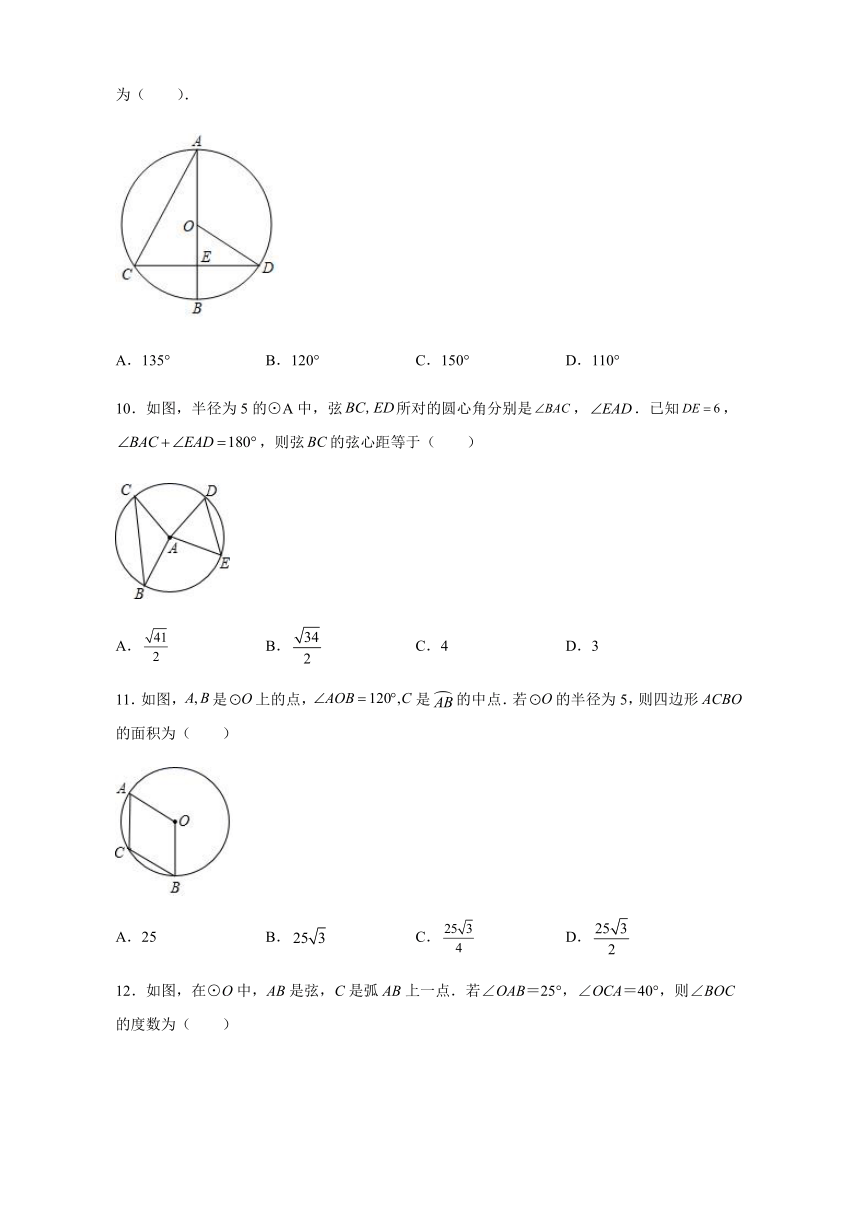
9.如图,为的直径,为弦,,垂足为E,若,则的度数为( ).
A.135° B.120° C.150° D.110°
10.如图,半径为5的⊙A中,弦所对的圆心角分别是,.已知,,则弦的弦心距等于( )
A. B. C.4 D.3
11.如图,是上的点,是的中点.若的半径为5,则四边形的面积为( )
A.25 B. C. D.
12.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
13.若一条弦把圆周分成的两段弧,则劣弧所对圆心角的度数是________.
14.如图,A、B、C是上三个点,,则弦与的大小关系是______.(填“>”、“<”或“=”)
15.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为_______.
16.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB=________.
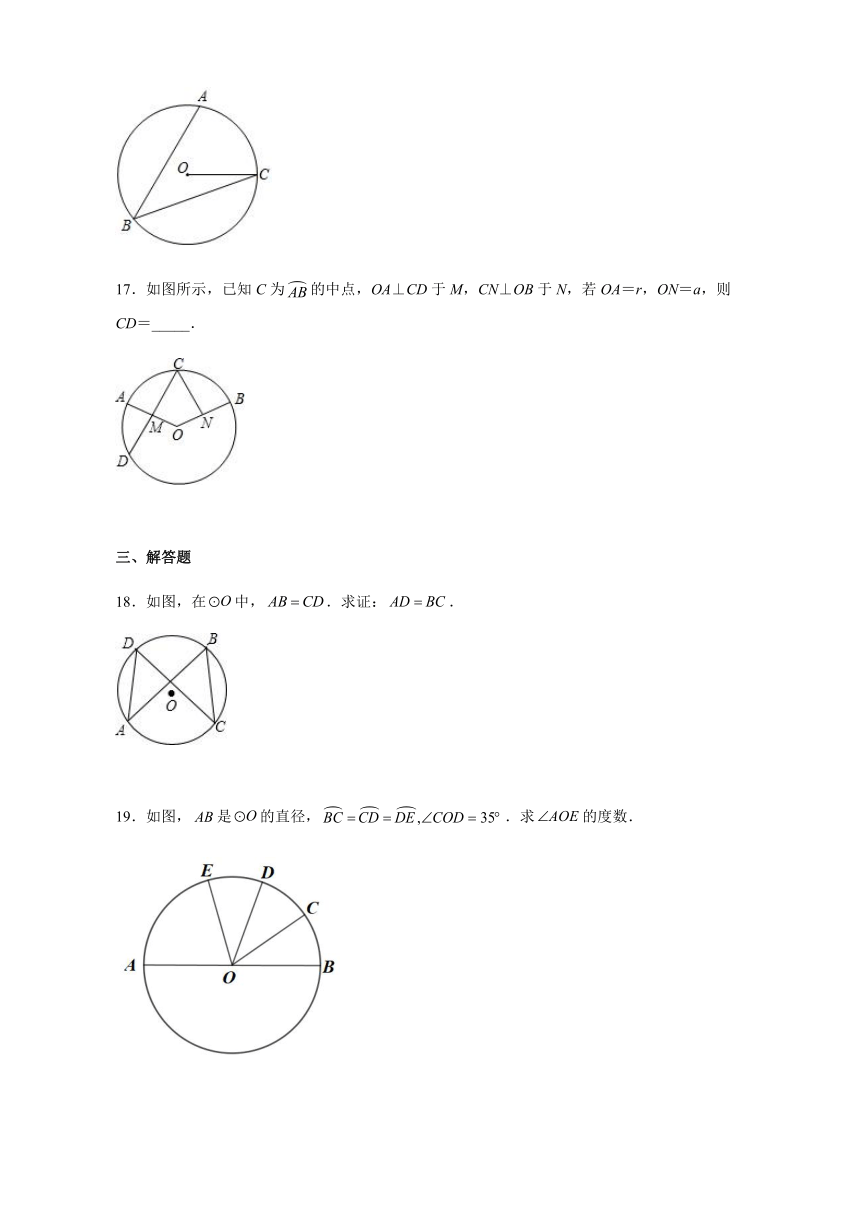
17.如图所示,已知C为的中点,OA⊥CD于M,CN⊥OB于N,若OA=r,ON=a,则CD=_____.
三、解答题
18.如图,在中,.求证:.
19.如图,是的直径,.求的度数.
20.如图,在中,,是两条弦,,,垂足分别为,.
(1)如果,那么与相等吗?说明理由;
(2)如果,那么与相等吗?与相等吗?与呢?
21.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且 .
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
参考答案
1.C
解:由题意可知:半径r=1,弦长为,
根据勾股定理的逆定理可知:()2=12+12,
∴长度等于的弦所对的弧有优弧、劣弧,
∴长度等于的弦所对弧的度数为90°或者270°.
故选C.
2.B
解:∵,
∴,
∴,
∵,
∴130°=2+50°,
∴=40°.
故选:B.
3.C
解:如图,,;
故选C.
4.C
解:∵,
∴,
∴,
故选:C.
5.C
解:∵OM=ON,
∴∠M=∠N=52°,
∴∠MON=180°-2×52°=76°.
故选C.
6.D
解:∵M、N分别是、的中点,
∴OM⊥AB,ON⊥AC,
∴∠AEO=∠AFO=90 ,
∵∠EAF=50 ,
∴∠MON=360 -∠AEO-∠AFO-∠EAF=360 -90 -90 -50 =130 ,
故选择:D.
7.C
解:如图;
以C为圆心,AC为半径作圆,交BD的延长线于E,连接AE、CE;
∵CB=CE,
∴∠CBE=∠CEB;
∵∠DAC=∠CBE,
∴∠DAC=∠CEB;
∵AC=CE,
∴∠CAE=∠CEA,
∴∠CAE﹣∠DAC=∠CEA﹣∠CED,即∠DAE=∠DEA;
∴AD=DE;
∵EC+BC>BE,EC=AC,BE=BD+DE=AD+BD,
∴AC+BC>BD+AD;
故选:C.
8.D
解:连接OB,∵四边形ABCO是平行四边形,
∴∠OAB=∠C=45°,
∵OA=OB,
∴∠OBA=∠OAB=45°,
∴∠AOB=90°,
∵DA=DA,
∴∠AOD=∠BOD=(360°﹣90°)=135°,
故选:D.
9.B
解:∵AB为⊙O的直径,CD为弦,CD⊥AB,
∴,
∴∠BOD=2∠BAC=60°,
∴∠AOD=180°-∠BOD=120°,
故选:B.
10.D
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
而CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3,
故选:D.
11.D
解:如图所示,连接OC,
∵C是的中点,
∴,
∴∠AOC=∠BOC,
∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵OA=OB=OC,
∴△AOC和△BOC均为等边三角形,
∵的半径为5,
∴OA=AC=OC=5,
作OD⊥AC于D点,
∴OA=5,AD=,OD=,
∴,
∴,
故选:D.
12.A
解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
13.
解:∵一条弦把圆周分成的两段弧,
∴劣弧所对圆心角的度数为,
故答案为:.
14.<.
解:取中点为D,连结AD,BD,OD,
∴,
∴∠AOD=∠BOD=,
∵,
∴,
∴AD=BD=BC,
在△ABD中,AB<AD+BD=2AD=2BC.
故答案为<.
15.150°
解:连接OB,如图所示:
∵四边形ABCO是平行四边形,
∴∠OAB=∠C=60°,
∵OA=OB,
∴∠OBA=∠OAB=60°,
∴∠AOB=180°﹣60°﹣60°=60°,
∵DA=DB,
∴,
∴∠AOD=∠BOD=(360°﹣60°)=150°,
故答案为:150°.
16.20°
解:如图,连接AO,BO,
∴OA=OB=OC,
∴∠OBC=∠OCB,∠OAB=∠OBA,
∵AB=BC,
∴∠BOC=∠AOB,
∴,
∵∠ABC=40°,OB=OC,
∴∠OCB=∠OBC=20°.
故答案为:20°.
17.2
解:连接OC,
∵C为的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA,ON=a,
∴OM=ON=n,
∴CM==,
∵CM⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=2,
故答案为:2.
18.见解析
解:,
,
,
即,
.
19.75°
解:∵,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180° ∠EOD ∠COD ∠BOC=75°.
20.(1)相等,见解析;(2),,,见解析
解:(1)OE=OF,
理由是:∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD,
∵∠AOB=∠COD,
∴∠EOB=∠FOD,
∵在△EOB和△FOD中,
∴△EOB≌△FOD(AAS),
∴OE=OF.;
(2),,.
理由:∵,,
∴,
又∵,,∴,
∴,
∵,,,,
∴,,
∴,∴,.
21.(1)见解析;(2).
解:(1)连接OA、OB,如图1所示:
∵OA=OB,
∴∠A=∠B,
∵,
∴∠AOE=∠BOF,
在△AOE和△OBF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)连接OA,如图2所示:
∵OM⊥AB,
∴AM=AB=6,
设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得:62+x2=(x+3)2,
解得:x=,
∴OM=.
一、单选题
1.在半径为的圆中,长度等于的弦所对的弧的度数为( )
A. B. C.或 D.或
2.如图,在⊙O中,,,,则的度数是( )
A. B. C. D.
3.如图所示,C是⊙O上一点,若,则∠AOB的度数为( )
A.20° B.40° C.80° D.140°
4.如图,AB是⊙O的直径,,,则=( )
A.30° B.45° C.60° D.以上都不正确
5.如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为( )
A.38° B.52° C.76° D.104°
6.如图所示,⊙O的弦AB、AC的夹角为50°,M、N分别是、的中点,则∠MON的度数是( )
A.100° B.110° C.120° D.130°
7.在⊙O中,C是的中点,D是上的任一点(与点A、C不重合),则( )
A.AC+CB=AD+DB B.AC+CB<AD+DB
C.AC+CB>AD+DB D.AC+CB与AD+DB的大小关系不确定
8.如图,在平行四边形ABCO中,,点A,B在⊙O上,点D在优弧ADB上,,则的度数为( )
A.165° B.155° C.145° D.135°
9.如图,为的直径,为弦,,垂足为E,若,则的度数为( ).
A.135° B.120° C.150° D.110°
10.如图,半径为5的⊙A中,弦所对的圆心角分别是,.已知,,则弦的弦心距等于( )
A. B. C.4 D.3
11.如图,是上的点,是的中点.若的半径为5,则四边形的面积为( )
A.25 B. C. D.
12.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
13.若一条弦把圆周分成的两段弧,则劣弧所对圆心角的度数是________.
14.如图,A、B、C是上三个点,,则弦与的大小关系是______.(填“>”、“<”或“=”)
15.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为_______.
16.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB=________.
17.如图所示,已知C为的中点,OA⊥CD于M,CN⊥OB于N,若OA=r,ON=a,则CD=_____.
三、解答题
18.如图,在中,.求证:.
19.如图,是的直径,.求的度数.
20.如图,在中,,是两条弦,,,垂足分别为,.
(1)如果,那么与相等吗?说明理由;
(2)如果,那么与相等吗?与相等吗?与呢?
21.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且 .
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
参考答案
1.C
解:由题意可知:半径r=1,弦长为,
根据勾股定理的逆定理可知:()2=12+12,
∴长度等于的弦所对的弧有优弧、劣弧,
∴长度等于的弦所对弧的度数为90°或者270°.
故选C.
2.B
解:∵,
∴,
∴,
∵,
∴130°=2+50°,
∴=40°.
故选:B.
3.C
解:如图,,;
故选C.
4.C
解:∵,
∴,
∴,
故选:C.
5.C
解:∵OM=ON,
∴∠M=∠N=52°,
∴∠MON=180°-2×52°=76°.
故选C.
6.D
解:∵M、N分别是、的中点,
∴OM⊥AB,ON⊥AC,
∴∠AEO=∠AFO=90 ,
∵∠EAF=50 ,
∴∠MON=360 -∠AEO-∠AFO-∠EAF=360 -90 -90 -50 =130 ,
故选择:D.
7.C
解:如图;
以C为圆心,AC为半径作圆,交BD的延长线于E,连接AE、CE;
∵CB=CE,
∴∠CBE=∠CEB;
∵∠DAC=∠CBE,
∴∠DAC=∠CEB;
∵AC=CE,
∴∠CAE=∠CEA,
∴∠CAE﹣∠DAC=∠CEA﹣∠CED,即∠DAE=∠DEA;
∴AD=DE;
∵EC+BC>BE,EC=AC,BE=BD+DE=AD+BD,
∴AC+BC>BD+AD;
故选:C.
8.D
解:连接OB,∵四边形ABCO是平行四边形,
∴∠OAB=∠C=45°,
∵OA=OB,
∴∠OBA=∠OAB=45°,
∴∠AOB=90°,
∵DA=DA,
∴∠AOD=∠BOD=(360°﹣90°)=135°,
故选:D.
9.B
解:∵AB为⊙O的直径,CD为弦,CD⊥AB,
∴,
∴∠BOD=2∠BAC=60°,
∴∠AOD=180°-∠BOD=120°,
故选:B.
10.D
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
而CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3,
故选:D.
11.D
解:如图所示,连接OC,
∵C是的中点,
∴,
∴∠AOC=∠BOC,
∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵OA=OB=OC,
∴△AOC和△BOC均为等边三角形,
∵的半径为5,
∴OA=AC=OC=5,
作OD⊥AC于D点,
∴OA=5,AD=,OD=,
∴,
∴,
故选:D.
12.A
解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
13.
解:∵一条弦把圆周分成的两段弧,
∴劣弧所对圆心角的度数为,
故答案为:.
14.<.
解:取中点为D,连结AD,BD,OD,
∴,
∴∠AOD=∠BOD=,
∵,
∴,
∴AD=BD=BC,
在△ABD中,AB<AD+BD=2AD=2BC.
故答案为<.
15.150°
解:连接OB,如图所示:
∵四边形ABCO是平行四边形,
∴∠OAB=∠C=60°,
∵OA=OB,
∴∠OBA=∠OAB=60°,
∴∠AOB=180°﹣60°﹣60°=60°,
∵DA=DB,
∴,
∴∠AOD=∠BOD=(360°﹣60°)=150°,
故答案为:150°.
16.20°
解:如图,连接AO,BO,
∴OA=OB=OC,
∴∠OBC=∠OCB,∠OAB=∠OBA,
∵AB=BC,
∴∠BOC=∠AOB,
∴,
∵∠ABC=40°,OB=OC,
∴∠OCB=∠OBC=20°.
故答案为:20°.
17.2
解:连接OC,
∵C为的中点,
∴=,
∴∠AOC=∠BOC,
∵CN⊥OB,CD⊥OA,ON=a,
∴OM=ON=n,
∴CM==,
∵CM⊥OA,
即OM⊥CD,
由垂径定理得:CD=2CM=2,
故答案为:2.
18.见解析
解:,
,
,
即,
.
19.75°
解:∵,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180° ∠EOD ∠COD ∠BOC=75°.
20.(1)相等,见解析;(2),,,见解析
解:(1)OE=OF,
理由是:∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD,
∵∠AOB=∠COD,
∴∠EOB=∠FOD,
∵在△EOB和△FOD中,
∴△EOB≌△FOD(AAS),
∴OE=OF.;
(2),,.
理由:∵,,
∴,
又∵,,∴,
∴,
∵,,,,
∴,,
∴,∴,.
21.(1)见解析;(2).
解:(1)连接OA、OB,如图1所示:
∵OA=OB,
∴∠A=∠B,
∵,
∴∠AOE=∠BOF,
在△AOE和△OBF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)连接OA,如图2所示:
∵OM⊥AB,
∴AM=AB=6,
设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得:62+x2=(x+3)2,
解得:x=,
∴OM=.
同课章节目录
