2021--2022学年浙教版九年级数学上册3.6圆内接四边形同步练习卷 (word版、含答案)
文档属性
| 名称 | 2021--2022学年浙教版九年级数学上册3.6圆内接四边形同步练习卷 (word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 20:37:52 | ||
图片预览


文档简介
2021年浙教版数学九年级上册
3.6《圆内接四边形》同步练习卷
一、选择题
1.圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
A. 20° B. 30° C. 70° D. 110°
2.如图,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( )
A.50° B.80° C.100° D.130°
3.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
4.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
A.40° B.60° C.70° D.80°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70° B.110° C.120° D.140°
6.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
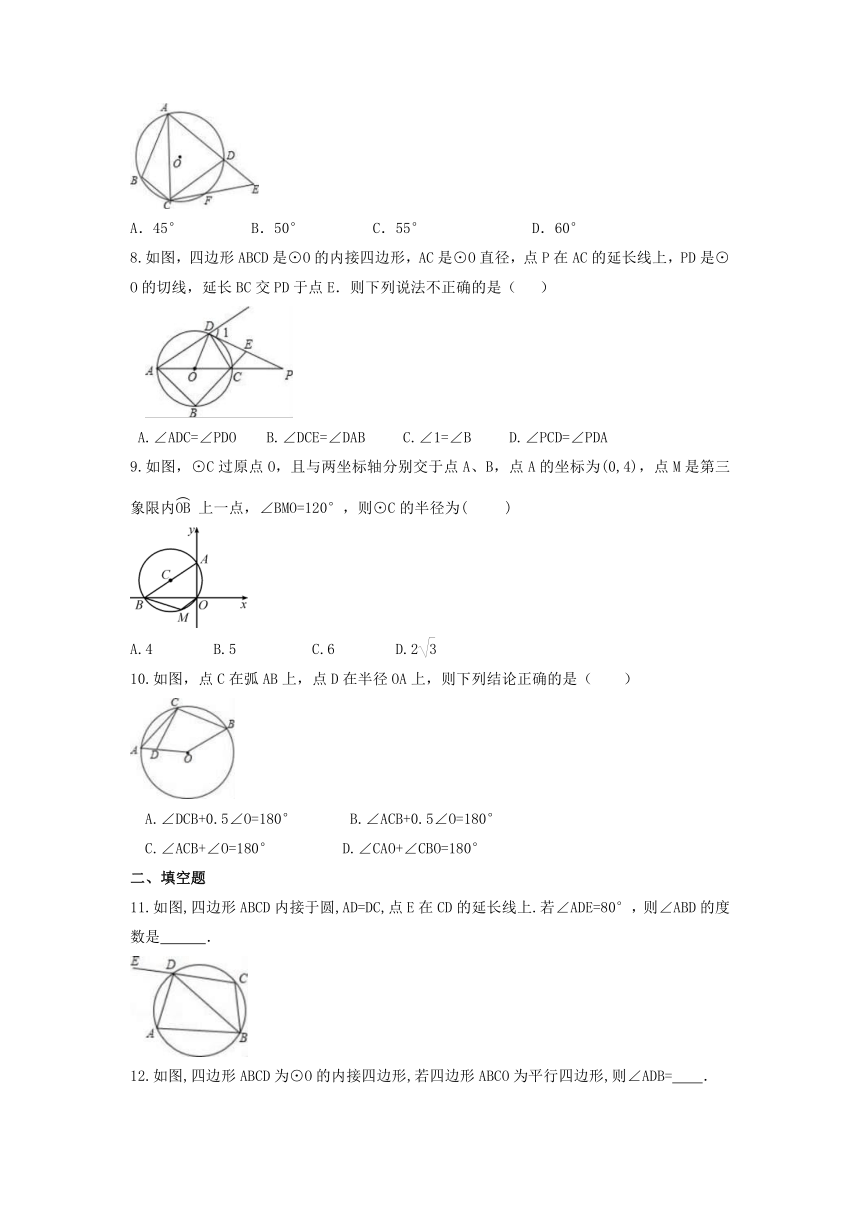
7.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
8.如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,点P在AC的延长线上,PD是⊙O的切线,延长BC交PD于点E.则下列说法不正确的是( )
A.∠ADC=∠PDO B.∠DCE=∠DAB C.∠1=∠B D.∠PCD=∠PDA
9.如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内上一点,∠BMO=120°,则⊙C的半径为( )
A.4 B.5 C.6 D.2
10.如图,点C在弧AB上,点D在半径OA上,则下列结论正确的是( )
A.∠DCB+0.5∠O=180° B.∠ACB+0.5∠O=180°
C.∠ACB+∠O=180° D.∠CAO+∠CBO=180°
二、填空题
11.如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是 .
12.如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB= .
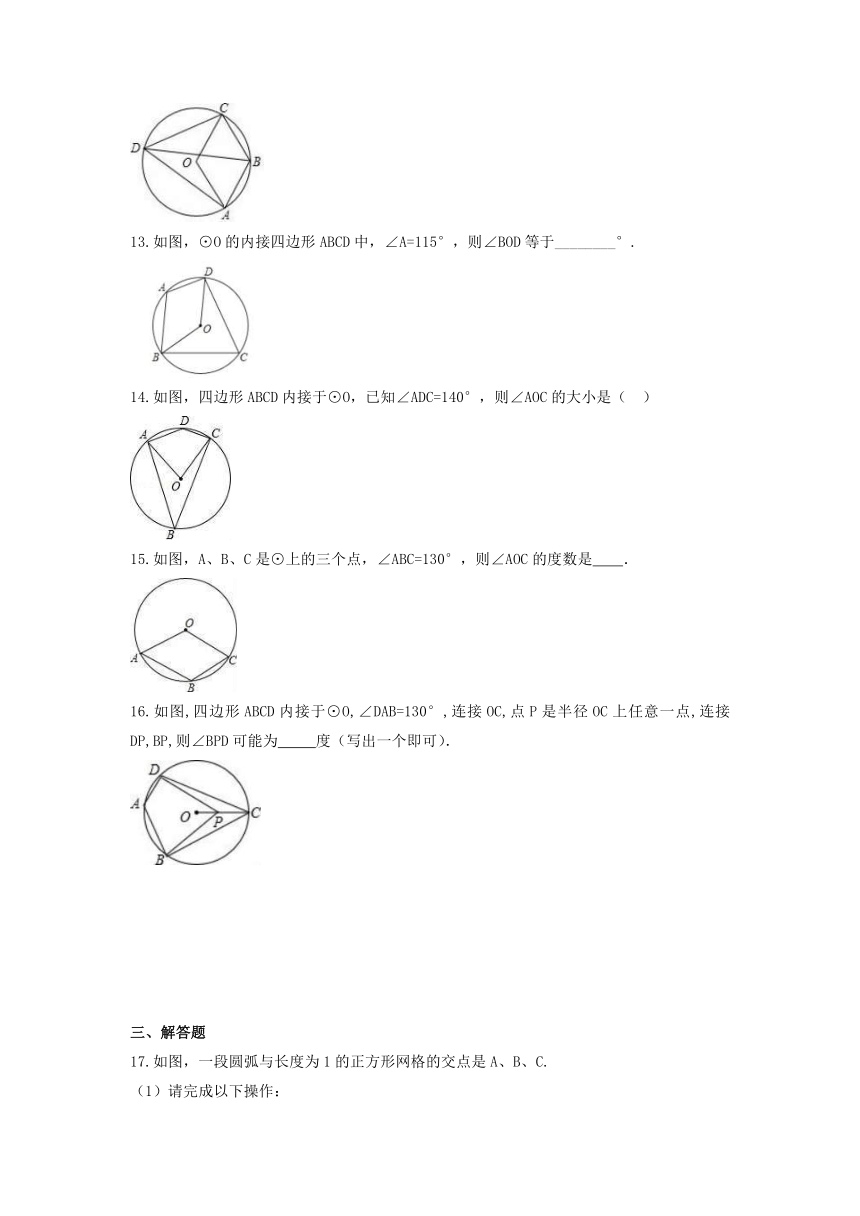
13.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于________°.
14.如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
15.如图,A、B、C是⊙上的三个点,∠ABC=130°,则∠AOC的度数是 .
16.如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为 度(写出一个即可).
三、解答题
17.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:⊙D的半径为 ;点(6,﹣2)在⊙D ;(填“上”、“内”、“外”)∠ADC的度数为 .
18.如图,已知四边形ABCD内接于⊙O,E是AD延长线上一点,且AC=BC.
求证:DC平分∠BDE。
19.已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.
(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数.
(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.
20.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:PD=PF;
(3)连接CD,若CD=3,BD=4,求⊙O的半径和DE的长.
21.如图,已知⊙O是△ABC的外接圆, =,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD.
求证:四边形AGCE是平行四边形.
参考答案
1.D
2.D
3.D
4.D
5.D
6.C
7.B.
8.C
9.A.
10.B
11.答案为:40°.
12.答案为:30°.
13.答案为:150°.
14.答案为:80°;
15.答案为:100°.
16.答案为:80.
17.解:(1)①平面直角坐标系如图所示:
②圆心点D,如图所示;
(2)⊙D的半径=AD==2,
∵点(6,﹣2)到圆心D的距离==2=半径,
∴点(6,﹣2)在⊙D上.观察图象可知:∠ADC=90°,
故答案为:2,上,90°.
18.
19.解:(Ⅰ)如图1,连接OC、OD,
∵CD=1,OC=OD=1,
∴△OCD为等边三角形,
∴∠COD=60°,
∴∠CBD=∠COD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠AEB=90°﹣∠DBE=90°﹣30°=60°;
(Ⅱ)如图2,连接OC、OD,同理可得∠CBD=30°,∠ADB=90°,
∴∠AEB=90°+∠DBE=90°+30°=120°.
20.(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA,
∵AB是⊙O的直径,DE⊥AB,
∴∠ADB=∠AED=90°,
∴∠ADE+∠DAE=90°,∠DBA+∠DAE=90°,
∴∠ADE=∠DBA,
∴∠DAC=∠ADE,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠ADE+∠EDB=∠DFA+∠DAC=90°,
又∵∠ADE=∠DAP,
∴∠PDF=∠PFD,
∴PD=PF;
(3)解:连接CD,
∵∠CBD=∠DBA,
∴CD=AD,
∵CD=3,∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.
即DE的长为2.4.
21.证明:(1)在⊙O中,∵=,
∴AB=AC,
∴∠B=∠ACB,
∵AE∥BC,
∴∠EAC=∠ACB,∴∠B=∠EAC,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(SAS),
∴AD=CE;
(2)连接AO并延长,交边BC于点H,
∵=,OA为半径,
∴AH⊥BC,
∴BH=CH,
∵AD=AG,
∴DH=HG,
∴BH﹣DH=CH﹣GH,即BD=CG,
∵BD=AE,
∴CG=AE,
∵CG∥AE,
∴四边形AGCE是平行四边形.
3.6《圆内接四边形》同步练习卷
一、选择题
1.圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
A. 20° B. 30° C. 70° D. 110°
2.如图,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( )
A.50° B.80° C.100° D.130°
3.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
4.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
A.40° B.60° C.70° D.80°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70° B.110° C.120° D.140°
6.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
7.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
8.如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,点P在AC的延长线上,PD是⊙O的切线,延长BC交PD于点E.则下列说法不正确的是( )
A.∠ADC=∠PDO B.∠DCE=∠DAB C.∠1=∠B D.∠PCD=∠PDA
9.如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内上一点,∠BMO=120°,则⊙C的半径为( )
A.4 B.5 C.6 D.2
10.如图,点C在弧AB上,点D在半径OA上,则下列结论正确的是( )
A.∠DCB+0.5∠O=180° B.∠ACB+0.5∠O=180°
C.∠ACB+∠O=180° D.∠CAO+∠CBO=180°
二、填空题
11.如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是 .
12.如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB= .
13.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于________°.
14.如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
15.如图,A、B、C是⊙上的三个点,∠ABC=130°,则∠AOC的度数是 .
16.如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为 度(写出一个即可).
三、解答题
17.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:⊙D的半径为 ;点(6,﹣2)在⊙D ;(填“上”、“内”、“外”)∠ADC的度数为 .
18.如图,已知四边形ABCD内接于⊙O,E是AD延长线上一点,且AC=BC.
求证:DC平分∠BDE。
19.已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.
(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数.
(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.
20.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:PD=PF;
(3)连接CD,若CD=3,BD=4,求⊙O的半径和DE的长.
21.如图,已知⊙O是△ABC的外接圆, =,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD.
求证:四边形AGCE是平行四边形.
参考答案
1.D
2.D
3.D
4.D
5.D
6.C
7.B.
8.C
9.A.
10.B
11.答案为:40°.
12.答案为:30°.
13.答案为:150°.
14.答案为:80°;
15.答案为:100°.
16.答案为:80.
17.解:(1)①平面直角坐标系如图所示:
②圆心点D,如图所示;
(2)⊙D的半径=AD==2,
∵点(6,﹣2)到圆心D的距离==2=半径,
∴点(6,﹣2)在⊙D上.观察图象可知:∠ADC=90°,
故答案为:2,上,90°.
18.
19.解:(Ⅰ)如图1,连接OC、OD,
∵CD=1,OC=OD=1,
∴△OCD为等边三角形,
∴∠COD=60°,
∴∠CBD=∠COD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠AEB=90°﹣∠DBE=90°﹣30°=60°;
(Ⅱ)如图2,连接OC、OD,同理可得∠CBD=30°,∠ADB=90°,
∴∠AEB=90°+∠DBE=90°+30°=120°.
20.(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA,
∵AB是⊙O的直径,DE⊥AB,
∴∠ADB=∠AED=90°,
∴∠ADE+∠DAE=90°,∠DBA+∠DAE=90°,
∴∠ADE=∠DBA,
∴∠DAC=∠ADE,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠ADE+∠EDB=∠DFA+∠DAC=90°,
又∵∠ADE=∠DAP,
∴∠PDF=∠PFD,
∴PD=PF;
(3)解:连接CD,
∵∠CBD=∠DBA,
∴CD=AD,
∵CD=3,∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.
即DE的长为2.4.
21.证明:(1)在⊙O中,∵=,
∴AB=AC,
∴∠B=∠ACB,
∵AE∥BC,
∴∠EAC=∠ACB,∴∠B=∠EAC,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(SAS),
∴AD=CE;
(2)连接AO并延长,交边BC于点H,
∵=,OA为半径,
∴AH⊥BC,
∴BH=CH,
∵AD=AG,
∴DH=HG,
∴BH﹣DH=CH﹣GH,即BD=CG,
∵BD=AE,
∴CG=AE,
∵CG∥AE,
∴四边形AGCE是平行四边形.
同课章节目录
