3.3垂径定理 同步练习题 2021-2022学年浙教版九年级数学上册(word版含答案)
文档属性
| 名称 | 3.3垂径定理 同步练习题 2021-2022学年浙教版九年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 297.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 21:19:56 | ||
图片预览
文档简介
2021-2022学年浙教版九年级数学上册《3.3垂径定理》同步练习题(附答案)
1.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
2.如图,⊙O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3≤OP≤5 B.4<OP<5 C.4≤OP≤5 D.3<OP<5
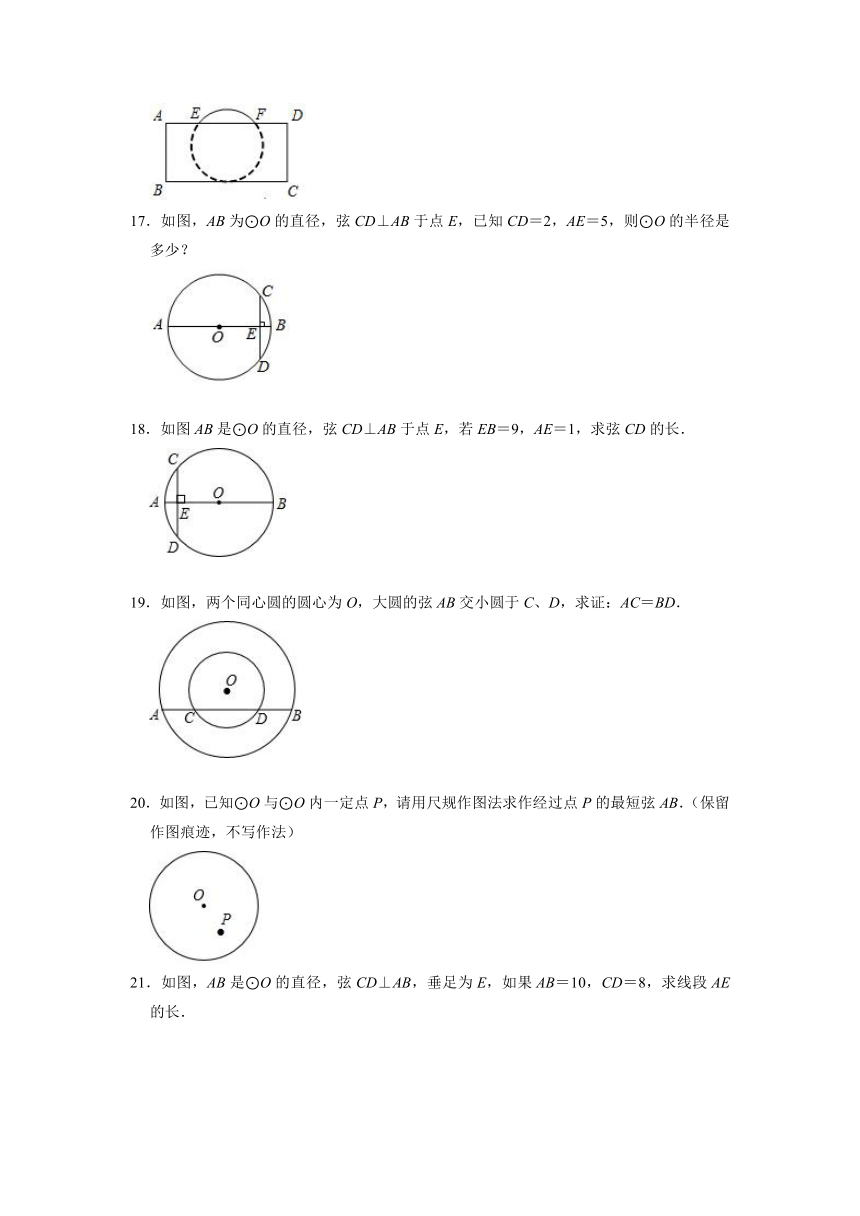
3.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A. B. C. D.
4.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( )
A.2cm B.3cm C.4cm D.5cm
5.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
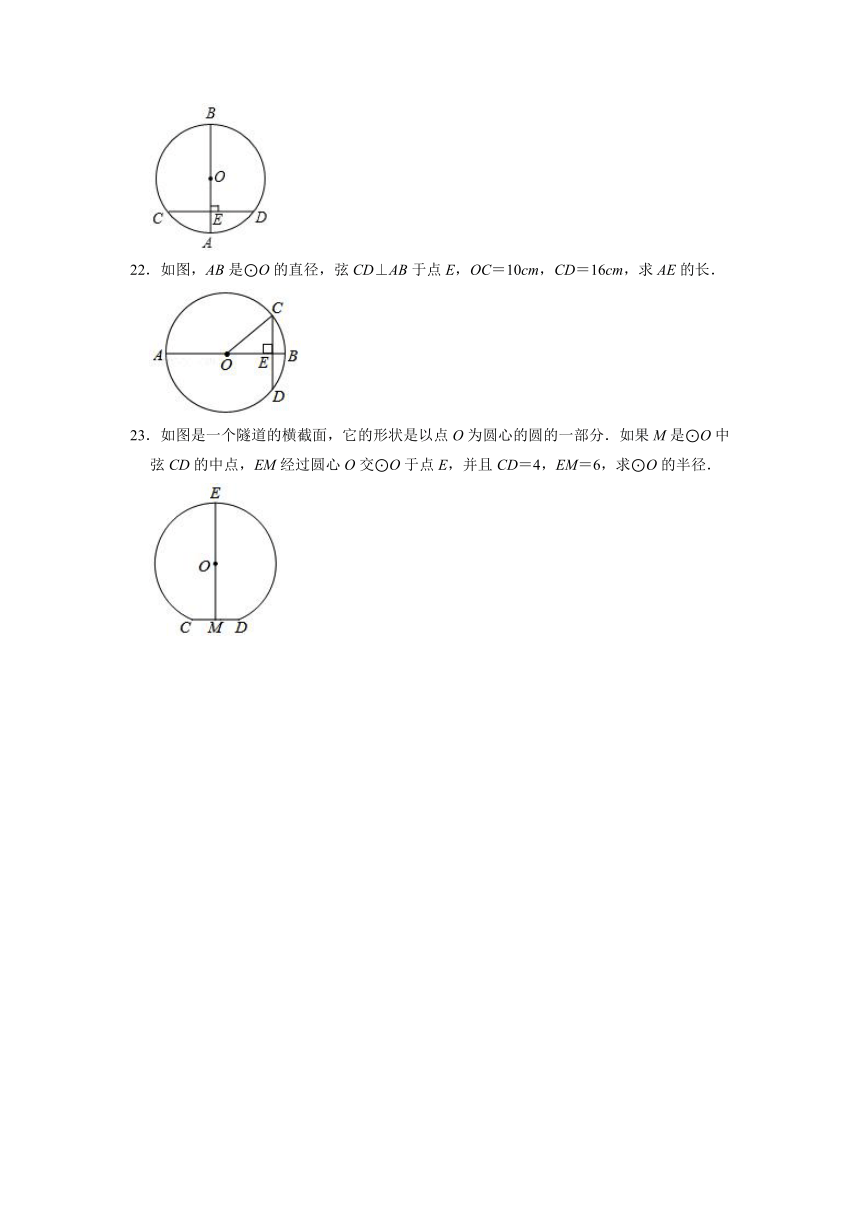
A.3 B.4 C.5 D.6
6.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若CD=BP=8,则⊙O的直径为( )
A.10 B.8 C.5 D.3
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10 B.8 C.5 D.3
8.如图,⊙O的直径CD为10,弦AB的长为8,且AB⊥CD,垂足为M,则CM的长为( )
A.1 B.2 C.3 D.4
9.如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C.3 D.4
10.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm B.4mm C.5mm D.8mm
11.如图,在⊙O中,直径AB=10,弦CD⊥AB,交直径AB于点E,CD=6,则EB= .
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2m,水面宽AB为8m,则输水管的半径为 m.
13.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
14.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,EB=2,则⊙O的半径为 .
15.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
16.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
17.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=2,AE=5,则⊙O的半径是多少?
18.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
19.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
20.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
21.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
22.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=10cm,CD=16cm,求AE的长.
23.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4,EM=6,求⊙O的半径.
参考答案
1.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
2.解:连接OA,过点O作OH⊥AB于H,
则AH=HB=AB=3,
由勾股定理得,OH==4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:C.
3.解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD∥BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH=EF=1,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:r2﹣(2﹣r)2=12,
解得:r=,
即球的半径长为,
故选:C.
4.解:连接OA,则OA=10cm,
∵OC⊥AB,OC过O,AB=16cm,
∴∠ODA=90°,AD=BD=8cm,
在Rt△ODA中,由勾股定理得:OD===6(cm),
∵OC=10cm,
∴CD=OC﹣OD=4cm,
故选:C.
5.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
6.解:连接OD,
∵CD⊥AB,CD=8,
∴PD=CD=×8=4,
在Rt△ODP中,设OD=x,则OB=x,
∵PD=4,OP=BP﹣OB=8﹣x,
∴OD2=PD2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
7.解:连接OC,
∵CD⊥AB,CD=8,
∴PC=CD=×8=4,
在Rt△OCP中,设OC=x,则OA=x,
∵PC=4,OP=AP﹣OA=8﹣x,
∴OC2=PC2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
8.解:连接OA.
∵直径CD⊥AB,AB=8,
∴AM=BM=AB=4,
在Rt△AOM中,OA=5,AM=4,
根据勾股定理得:OM==3,
则CM=OC﹣OM=5﹣3=2,
故选:B.
9.解:连接OB,作OE⊥AB于E,OF⊥CD于F,
则BE=AB=4,四边形PEOF为矩形,
∵AB=CD,OE⊥AB,OF⊥CD,
∴OE=OF,
∴矩形PEOF为正方形,
∴OE=PE,
在Rt△OEB中,OE==3,
∴OP==3,
故选:C.
10.解:连接OA,
∵OD⊥AB,
∴AD=AB=4(mm),
由勾股定理得,OA==5(mm),
故选:C.
11.解:连接OC,如图所示:
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3,
在Rt△OEC中,∠OEC=90°,CE=3,OC=AB=5,
∴OE==4,
∴BE=OB﹣OE=AB﹣OE=5﹣4=1,
故答案为:1.
12.解:由题意得:OD⊥AB,
∴AC=AB=×8=4(m),
设OA=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
即r2=(r﹣2)2+42,
解得:r=5,
即输水管的半径为5m,
故答案为:5.
13.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
14.解:连接OC,
设⊙O的半径为R,则OE=R﹣2,
∵CD⊥AB,
∴CE=CD=4,
由勾股定理得,OC2=OE2+CE2,即R2=(R﹣2)2+42,
解得,R=5,
则⊙O的半径为5,
故答案为:5.
15.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
16.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
17.解:连接OD,设⊙O的半径为r,
∵AB为⊙O的直径,弦CD⊥AB,CD=2,AE=5,
∴DE=1,OE=5﹣r,
在Rt△ODE中,OD2=OE2+DE2,即r2=(5﹣r)2+1,
解得,r=2.6,
答:⊙O的半径是2.6.
18.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE==3,
∴CD=2CE=6.
19.证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
20.解:如图所示:线段AB即为所求;
21.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
22.解:∵弦CD⊥AB于点E,CD=16cm,
∴CE=CD=8cm.
在Rt△OCE中,OC=10cm,CE=8cm,
∴OE===6(cm),
∴AE=AO+OE=10+6=16(cm).
23.解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
1.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
2.如图,⊙O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3≤OP≤5 B.4<OP<5 C.4≤OP≤5 D.3<OP<5
3.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A. B. C. D.
4.如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( )
A.2cm B.3cm C.4cm D.5cm
5.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
A.3 B.4 C.5 D.6
6.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若CD=BP=8,则⊙O的直径为( )
A.10 B.8 C.5 D.3
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=AP=8,则⊙O的直径为( )
A.10 B.8 C.5 D.3
8.如图,⊙O的直径CD为10,弦AB的长为8,且AB⊥CD,垂足为M,则CM的长为( )
A.1 B.2 C.3 D.4
9.如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C.3 D.4
10.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm B.4mm C.5mm D.8mm
11.如图,在⊙O中,直径AB=10,弦CD⊥AB,交直径AB于点E,CD=6,则EB= .
12.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2m,水面宽AB为8m,则输水管的半径为 m.
13.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
14.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,EB=2,则⊙O的半径为 .
15.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
16.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
17.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=2,AE=5,则⊙O的半径是多少?
18.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
19.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
20.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
21.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
22.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=10cm,CD=16cm,求AE的长.
23.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4,EM=6,求⊙O的半径.
参考答案
1.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
2.解:连接OA,过点O作OH⊥AB于H,
则AH=HB=AB=3,
由勾股定理得,OH==4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:C.
3.解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD∥BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH=EF=1,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:r2﹣(2﹣r)2=12,
解得:r=,
即球的半径长为,
故选:C.
4.解:连接OA,则OA=10cm,
∵OC⊥AB,OC过O,AB=16cm,
∴∠ODA=90°,AD=BD=8cm,
在Rt△ODA中,由勾股定理得:OD===6(cm),
∵OC=10cm,
∴CD=OC﹣OD=4cm,
故选:C.
5.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
6.解:连接OD,
∵CD⊥AB,CD=8,
∴PD=CD=×8=4,
在Rt△ODP中,设OD=x,则OB=x,
∵PD=4,OP=BP﹣OB=8﹣x,
∴OD2=PD2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
7.解:连接OC,
∵CD⊥AB,CD=8,
∴PC=CD=×8=4,
在Rt△OCP中,设OC=x,则OA=x,
∵PC=4,OP=AP﹣OA=8﹣x,
∴OC2=PC2+OP2,
即x2=42+(8﹣x)2,
解得x=5,
∴⊙O的直径为10.
故选:A.
8.解:连接OA.
∵直径CD⊥AB,AB=8,
∴AM=BM=AB=4,
在Rt△AOM中,OA=5,AM=4,
根据勾股定理得:OM==3,
则CM=OC﹣OM=5﹣3=2,
故选:B.
9.解:连接OB,作OE⊥AB于E,OF⊥CD于F,
则BE=AB=4,四边形PEOF为矩形,
∵AB=CD,OE⊥AB,OF⊥CD,
∴OE=OF,
∴矩形PEOF为正方形,
∴OE=PE,
在Rt△OEB中,OE==3,
∴OP==3,
故选:C.
10.解:连接OA,
∵OD⊥AB,
∴AD=AB=4(mm),
由勾股定理得,OA==5(mm),
故选:C.
11.解:连接OC,如图所示:
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3,
在Rt△OEC中,∠OEC=90°,CE=3,OC=AB=5,
∴OE==4,
∴BE=OB﹣OE=AB﹣OE=5﹣4=1,
故答案为:1.
12.解:由题意得:OD⊥AB,
∴AC=AB=×8=4(m),
设OA=rm,则OC=OD﹣CD=(r﹣2)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
即r2=(r﹣2)2+42,
解得:r=5,
即输水管的半径为5m,
故答案为:5.
13.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
14.解:连接OC,
设⊙O的半径为R,则OE=R﹣2,
∵CD⊥AB,
∴CE=CD=4,
由勾股定理得,OC2=OE2+CE2,即R2=(R﹣2)2+42,
解得,R=5,
则⊙O的半径为5,
故答案为:5.
15.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
16.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
17.解:连接OD,设⊙O的半径为r,
∵AB为⊙O的直径,弦CD⊥AB,CD=2,AE=5,
∴DE=1,OE=5﹣r,
在Rt△ODE中,OD2=OE2+DE2,即r2=(5﹣r)2+1,
解得,r=2.6,
答:⊙O的半径是2.6.
18.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE==3,
∴CD=2CE=6.
19.证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
20.解:如图所示:线段AB即为所求;
21.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
22.解:∵弦CD⊥AB于点E,CD=16cm,
∴CE=CD=8cm.
在Rt△OCE中,OC=10cm,CE=8cm,
∴OE===6(cm),
∴AE=AO+OE=10+6=16(cm).
23.解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
同课章节目录
