1.3 解直角三角形 同步练习卷 浙教版数学九年级下册(word版含答案)
文档属性
| 名称 | 1.3 解直角三角形 同步练习卷 浙教版数学九年级下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 18:25:20 | ||
图片预览



文档简介
2021年浙教版数学九年级下册
1.3《解直角三角形》同步练习卷
一、选择题
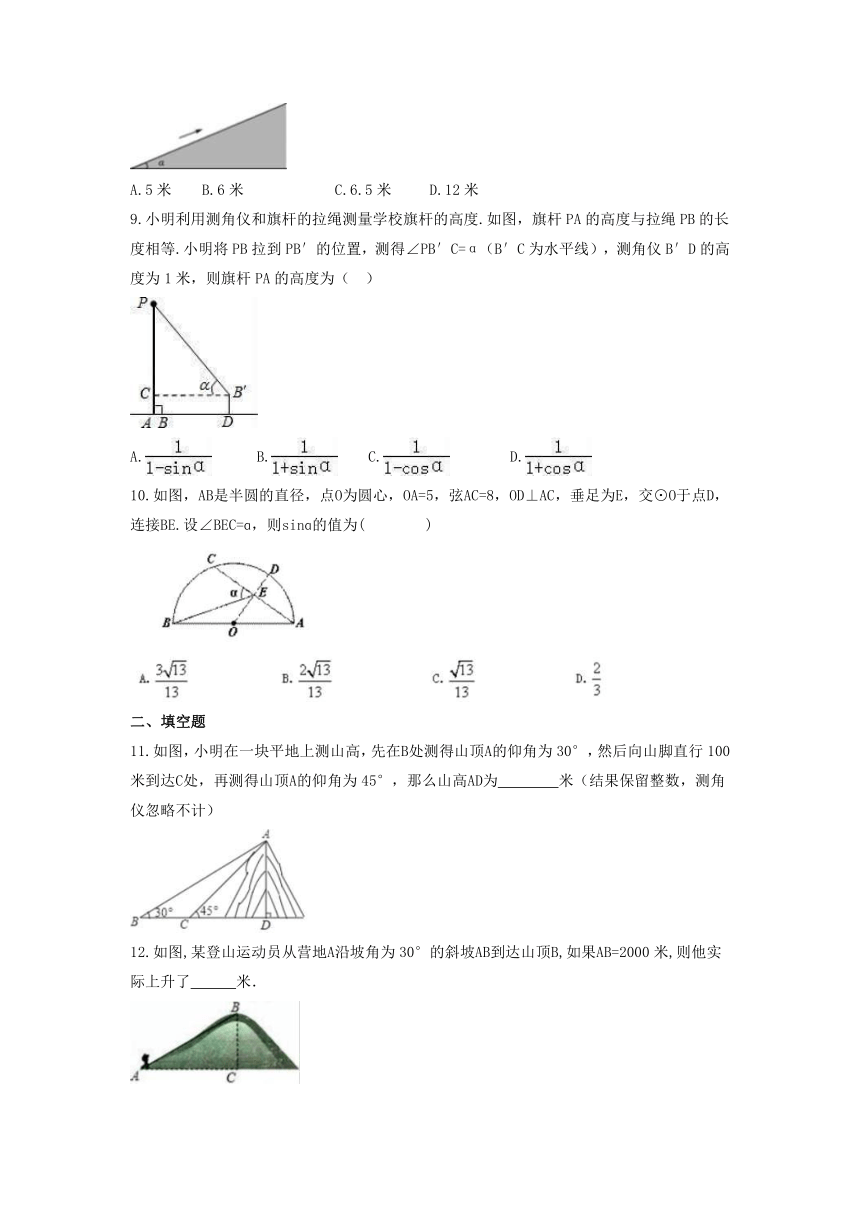
1.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
2.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
3.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.km B.km C.km D.km
4.周末,身高都为1.6 m的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角ɑ为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A,B两点的距离为30 m.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01)( )
A.36.21 m B.37.71 m C.40.98 m D.42.48 m
5.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2 C.(4+)米2 D.(4+4tanθ)米2
6.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin 35°米 B.100sin 55°米
C.100tan 35°米 D.100tan 55°米
7.如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.米 B.米 C.米 D.米
8.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cos α=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.12米
9.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A. B. C. D.
10.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=ɑ,则sinɑ的值为( )
二、填空题
11.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计)
12.如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
13.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
14.如图,河坝横断面迎水坡AB的坡比是1:,堤高BC=5米,则坝底AC的长度是 米.
15.如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为 米.(参考数据:≈1.41,≈1.73)
16.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
三、解答题
17.如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据≈1.414,≈1.732)
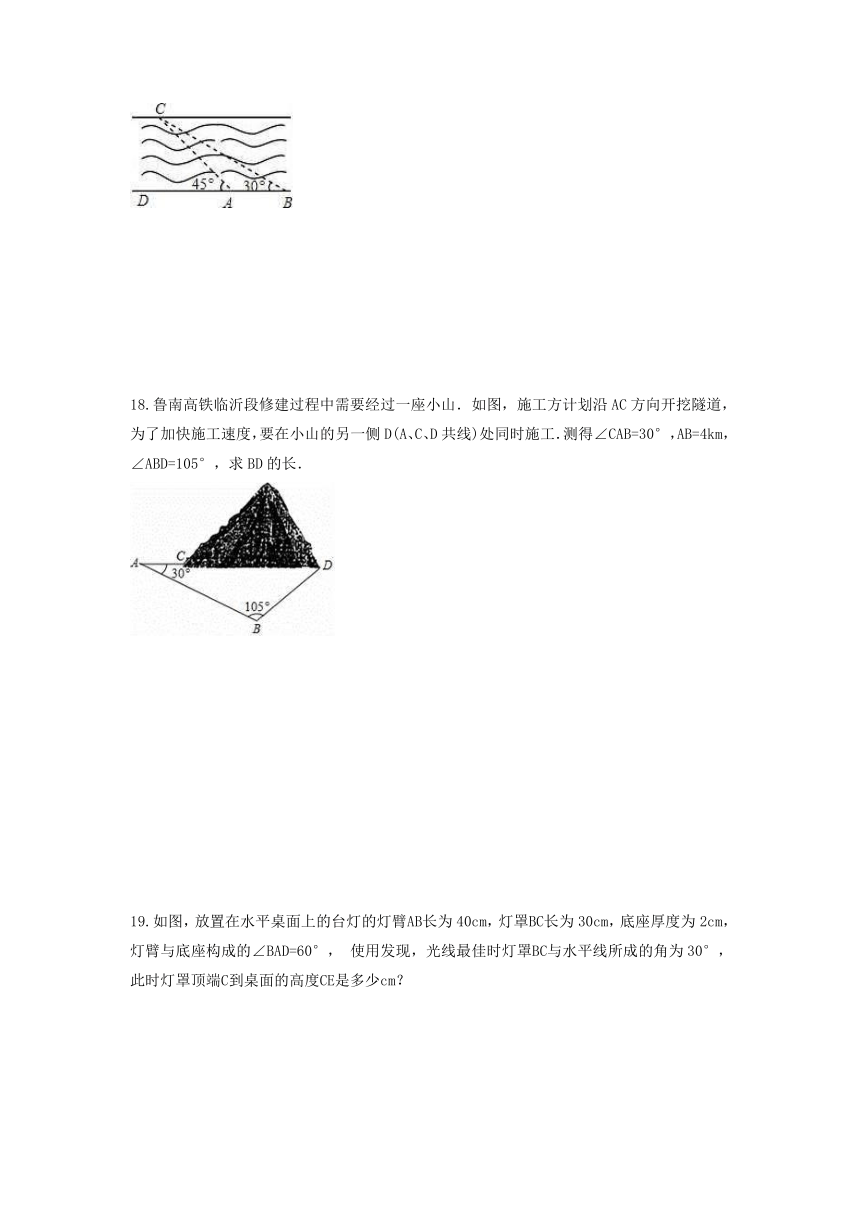
18.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,求BD的长.
19.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°, 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
20.如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若=,求sinE的值.
21.某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(参考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,1.73)
参考答案
1.C
2.A
3.B
4.D
5.D
6.C;
7.B
8.A;
9.A
10.A
11.答案为:137.
12.答案为:1000.
13.答案为:(5+5).
14.答案为:.
15.答案为:18.8米
16.答案为:
17.解:过C作CE⊥AB于E,设CE=x米,在Rt△AEC中:∠CAE=45°,AE=CE=x
在Rt△BCE中:∠CBE=30°,BE=CE=x,∴x=x+50解之得:x=25+25≈68.30.
答:河宽为68.30米.
18.解:作BE⊥AD于点E,
∵∠CAB=30°,AB=4km,
∴∠ABE=60°,BE=2km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=2km,
∴BD==2km,
即BD的长是2km.
19.解:过点B作BM⊥CE于点M,BF⊥DA于点F,如图所示.
在Rt△BCM中,BC=30cm,∠CBM=30°,
∴CM=BC sin∠CBM=15cm.
在Rt△ABF中,AB=40cm,∠BAD=60°,
∴BF=AB sin∠BAD=20cm.
∵∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2=20+17(cm).
答:此时灯罩顶端C到桌面的高度CE是(20+17)cm.
20.(1)证明:连接OC,如图①.
∵OC切半圆O于C,
∴OC⊥DC,
又AD⊥CD.
∴OC∥AD.
∴∠OCA=∠DAC.
∵OC=OA,
∴∠OAC=∠ACO.
∴∠DAC=∠CAO,即AC平分∠DAB.
(2)解:在Rt△OCE中,∵OC=OB=OE,∴∠E=30°.
∴在Rt△OCF中,CF=OC·sin60°=2×=.
(3)解:连接OC,如图②.
∵CO∥AD,∴△CGO∽△AGD.∴==.
不妨设CO=AO=3k,则AD=4k.
又△COE∽△DAE,∴===.∴EO=9k.
在Rt△COE中,sinE===.
21.解:(1)过点C作CG⊥AM于点G,如图1,
∵AB⊥AM,DE⊥AM,∴AB∥CG∥DE,∴∠DCG=180°﹣∠CDE=110°,
∴BCG=∠BCD﹣∠GCD=30°,∴∠ABC=180°﹣∠BCG=150°;
(2)过点C作CP⊥DE于点P,过点B作BQ⊥DE于点Q,交CG于点N,如图2,
在Rt△CPD中,DP=CP×cos70°≈0.51(米),
在Rt△BCN中,CN=BC×cos30°≈1.04(米),
所以,DE=DP+PQ+QE=DP+CN+AB=2.35(米),
如图3,过点D作DH⊥AM于点H,过点C作CK⊥DH于点K,
在Rt△CKD中,DK=CD×cos50°≈1.16(米),所以,DH=DK+KH=3.16(米),
所以,DH﹣DE=0.8(米),
所以,斗杆顶点D的最高点比初始位置高了0.8米.
1.3《解直角三角形》同步练习卷
一、选择题
1.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
2.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
3.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.km B.km C.km D.km
4.周末,身高都为1.6 m的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角ɑ为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A,B两点的距离为30 m.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01)( )
A.36.21 m B.37.71 m C.40.98 m D.42.48 m
5.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2 C.(4+)米2 D.(4+4tanθ)米2
6.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
A.100sin 35°米 B.100sin 55°米
C.100tan 35°米 D.100tan 55°米
7.如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.米 B.米 C.米 D.米
8.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cos α=,则小车上升的高度是( )
A.5米 B.6米 C.6.5米 D.12米
9.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A. B. C. D.
10.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=ɑ,则sinɑ的值为( )
二、填空题
11.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计)
12.如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
13.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
14.如图,河坝横断面迎水坡AB的坡比是1:,堤高BC=5米,则坝底AC的长度是 米.
15.如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为 米.(参考数据:≈1.41,≈1.73)
16.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
三、解答题
17.如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据≈1.414,≈1.732)
18.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,求BD的长.
19.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°, 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
20.如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若=,求sinE的值.
21.某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(参考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,1.73)
参考答案
1.C
2.A
3.B
4.D
5.D
6.C;
7.B
8.A;
9.A
10.A
11.答案为:137.
12.答案为:1000.
13.答案为:(5+5).
14.答案为:.
15.答案为:18.8米
16.答案为:
17.解:过C作CE⊥AB于E,设CE=x米,在Rt△AEC中:∠CAE=45°,AE=CE=x
在Rt△BCE中:∠CBE=30°,BE=CE=x,∴x=x+50解之得:x=25+25≈68.30.
答:河宽为68.30米.
18.解:作BE⊥AD于点E,
∵∠CAB=30°,AB=4km,
∴∠ABE=60°,BE=2km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=2km,
∴BD==2km,
即BD的长是2km.
19.解:过点B作BM⊥CE于点M,BF⊥DA于点F,如图所示.
在Rt△BCM中,BC=30cm,∠CBM=30°,
∴CM=BC sin∠CBM=15cm.
在Rt△ABF中,AB=40cm,∠BAD=60°,
∴BF=AB sin∠BAD=20cm.
∵∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2=20+17(cm).
答:此时灯罩顶端C到桌面的高度CE是(20+17)cm.
20.(1)证明:连接OC,如图①.
∵OC切半圆O于C,
∴OC⊥DC,
又AD⊥CD.
∴OC∥AD.
∴∠OCA=∠DAC.
∵OC=OA,
∴∠OAC=∠ACO.
∴∠DAC=∠CAO,即AC平分∠DAB.
(2)解:在Rt△OCE中,∵OC=OB=OE,∴∠E=30°.
∴在Rt△OCF中,CF=OC·sin60°=2×=.
(3)解:连接OC,如图②.
∵CO∥AD,∴△CGO∽△AGD.∴==.
不妨设CO=AO=3k,则AD=4k.
又△COE∽△DAE,∴===.∴EO=9k.
在Rt△COE中,sinE===.
21.解:(1)过点C作CG⊥AM于点G,如图1,
∵AB⊥AM,DE⊥AM,∴AB∥CG∥DE,∴∠DCG=180°﹣∠CDE=110°,
∴BCG=∠BCD﹣∠GCD=30°,∴∠ABC=180°﹣∠BCG=150°;
(2)过点C作CP⊥DE于点P,过点B作BQ⊥DE于点Q,交CG于点N,如图2,
在Rt△CPD中,DP=CP×cos70°≈0.51(米),
在Rt△BCN中,CN=BC×cos30°≈1.04(米),
所以,DE=DP+PQ+QE=DP+CN+AB=2.35(米),
如图3,过点D作DH⊥AM于点H,过点C作CK⊥DH于点K,
在Rt△CKD中,DK=CD×cos50°≈1.16(米),所以,DH=DK+KH=3.16(米),
所以,DH﹣DE=0.8(米),
所以,斗杆顶点D的最高点比初始位置高了0.8米.
