2.1二次函数

(共20张PPT)
温故知新
我们已经学习了哪些函数？
正比例函数　y=kx 　 (k是常数，k≠0)
一次函数　y=kx+b (k,b 是常数，且k≠0)
反比例函数 　　 (k是常数，k≠0)
一元二次方程的一般形式是？
ax2+bx+c=0 (a,b,c是常数，a≠0)
请用适当的函数解析式表示下列问题情境中的两个变量y与x之间的关系：
(1)圆的面积 y (cm2)与圆的半径 x ( cm )
y =πx2
(2)王先生存人银行2万元,先存一个一年定期，一年后银行将本息自动转存为又一个一年定期,设一年定期的年存款利率为x ,两年后王先生共得本息y元;
y = 20000(1+x)2
合作学习:
(3)拟建中的一个温室的平面图如图,如果温室外围是一个矩形，周长为12Om , 室内通道的尺寸如图,设一条边长为 x (cm), 种植面积为 y (m2)·
1
1
1
3
x
y = (60-x-4)(x-2)
这些关系中
y是x的什么函数？
1、y =πx2
2、y = 2(1+x)2
3、y = (60-x-4)(x-2)
=2x2+4x+2
=-x2+58x-112
上述三个问题中的函数解析式具有哪些共同的特征
经化简后都具y=ax +bx+c 的形式.
(a,b,c是常数, )
a≠0
合作探究
二次函数y=ax +bx+c中a≠0,但b、c可以为0.
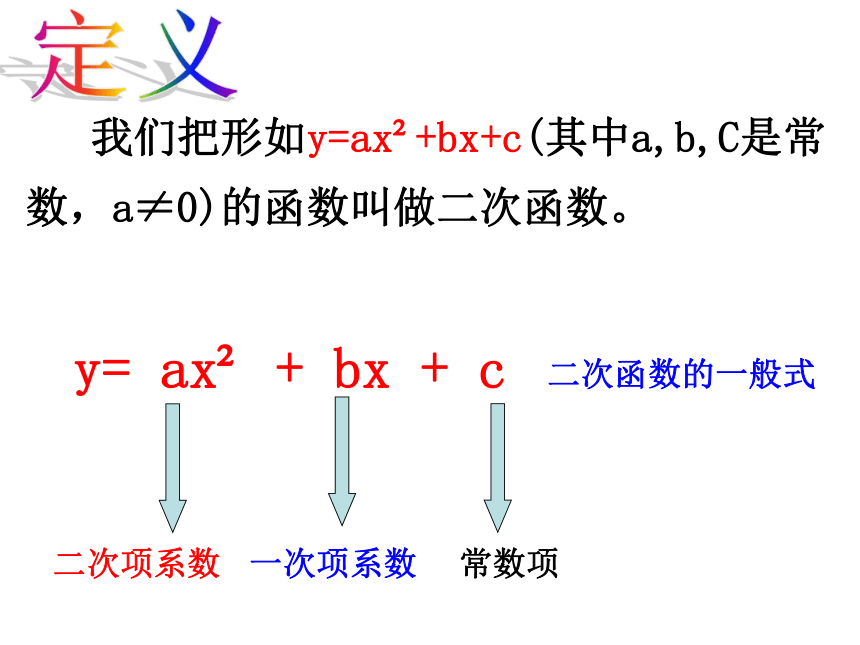
我们把形如y=ax +bx+c(其中a,b,C是常数，a≠0)的函数叫做二次函数。
y= ax + bx + c
二次项系数
一次项系数
常数项
二次函数的一般式
二次函数的特殊形式：
当b＝0时， y＝ax2＋c
当c＝0时， y＝ax2＋bx
当b＝0，c＝0时， y＝ax2
例如，
1、二次函数 y=-x2+58x-112 的
二次项系数为 ，
一次项系数为 ，
常数项 。
2、二次涵数y=πx2的
二次项系数 ,
一次项系数 ，
常数项 。
a=-1
b=58
c=-112
a=π
b=0
c=0
下列函数中,哪些是二次函数
是
不是
是
是
不是
辨一辨
下列函数中,哪些是二次函数
辨一辨
)
1
)(
1
(
)
1
(
)
5
(
2
-
+
-
-
=
x
x
x
y
)
1
(
)
4
(
-
=
x
x
y
1
2
)
3
(
2
-
-
=
x
x
y
1
)
2
(
2
-
=
x
y
)
1
(
2
=
x
y
　　
分别说出这些二次函数的二次项系数a、一次项系数b和常数项c：
　　说明：要确定二次函数的二次项系数、一次项系数和常数项，必须先将二次函数化简为y= ax2+bx+c形式。并按自变量的次数从高到低排列.
例1、如图，一张正方形纸板的边长为2cm，将它剪去4个全等 的直角三角形 (图中阴影部分 )，设AE=BF =CG=DH=x(cm)，四边形 EFGH的面积为y(cm2)，求 :
(l) y关于x的函数解析式和自变量x的取值范围 ;
(2 )当 x分别为0.25，0.5，1，1.5，1.75时 ，
对应的四边形EFGH 的面积，并列表表示.
A
B
E
F
C
G
D
H
X
X
X
X
2–X
2–X
2–X
2–X
y=22-4x（2-x）÷2
=2x2-4x+4
解：（1）由已知得：
(0＜x＜2)
即所求函数解析式为y=2x2-4x+4
注意:当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范围.
(2 )当 x分别为0.25，0.5，1，1.5，1.75时 ，
对应的四边形 EFGH的 面积，并列表表示.
y=2x2-4x+4 (0＜x＜2)
(2)解:当x=0.25时,y=2×0.252-4×0.25+4=3.125(cm2)
列表如下:
x(cm) 0.25 0.5 1 1.5 1.75
y(cm2) 3.125 2.5 2 2.5 3.125
依次计算可得：当x=0.5时, y=2.5(cm2)
当x=1时, y=2(cm2)
当x=1.5时, y=2.5（cm2)
当x=1.75时, y=3.125(cm2)
写出下列二次函数的二次项系数、一次项系数和常数项：
练一练:
函数解析式 二次项系数 一次项系数 常数项
练一练
　用20米的篱笆围成一边靠墙矩形花圃，如图，设连墙的一边为x,矩形的面积为y,求：
　(1)写出y关于x的函数关系式
和自变量x的取值范围。　　　　　　　　　
　(2)当x=3时,矩形的面积为多少
x
(２)当x=3时
自变量x的取值范围(0例２、已知二次函数y=x +px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.
｛
待定系数法
1、已知二次函数y=ax +bx+3, 当x=2时,函数值为3, 当x= - 2时, 函数值为2, 求这个二次函数的解析式.
做一做
2、已知关于x的二次函数,当x=－1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
｛
做一做
当m取何值时，函数是y= (m+2)x
是一次函数？
m2-2
二次函数？
课 外 拓 展
反比例函数？
想一想:
心理学家研究发现：一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力y随时间t的变化规律有如下关系式：
（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？
（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？
（3）一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目.
课 外 拓 展