《3.7正多边形》同步练习 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 《3.7正多边形》同步练习 2021-2022学年浙教版九年级数学上册(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 572.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《3.7正多边形》同步练习题(附答案)
1.已知一个正六边形的边心距为,则它的外接圆的面积为( )
A.4π B.3π C.2π D.π
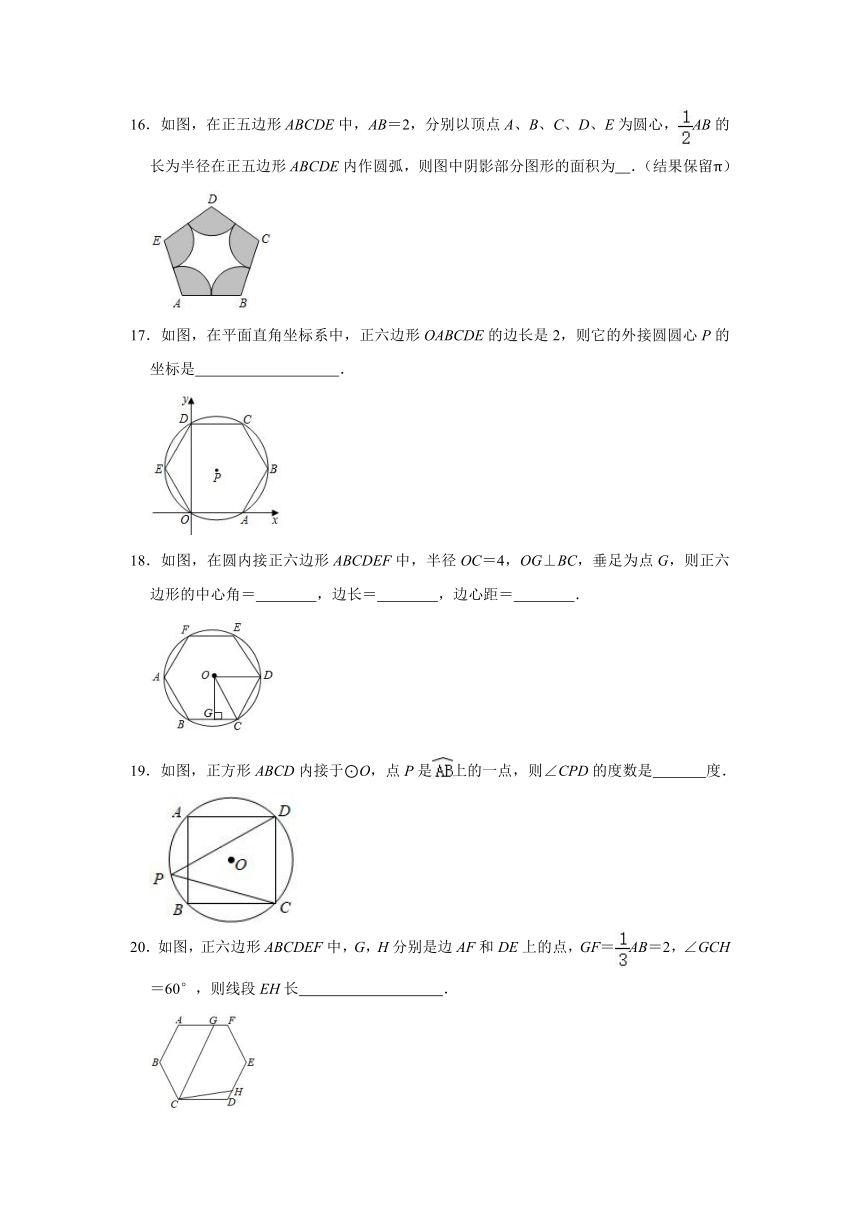
2.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
3.如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A. B. C.2 D.
4.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2 B. C.2 D.2
5.正方形外接圆的半径为4,则其内切圆的半径为( )
A.2 B. C.1 D.
6.如图,将边长为6的正六边形ABCDEF沿HG折叠,点B的对应点B′恰好落在边AF的中点上,点C、D的对应点为C′、D′,延长B′C′交EF于点M,则C′M的长为( )
A.1 B.
C. D.
7.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A. B. C. D.
8.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A.10 B.9 C.8 D.7
9.如图,用n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )
A.5 B.6 C.8 D.10
10.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2: B.: C.: D.:2
11.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点.则点O是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
12.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2 B. C.3 D.
13.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则等于( )
A.3 B. C.2 D.
14.如图,点A、B、C、D、E、F是⊙O的等分点,分别以点B、D、F为圆心,AF的长为半径画弧,形成美丽的“三叶轮”图案.已知⊙O的半径为1,那么“三叶轮”图案的面积为( )
A. B. C. D.
15.如图,正六边形的边长为4,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 .
16.如图,在正五边形ABCDE中,AB=2,分别以顶点A、B、C、D、E为圆心,AB的长为半径在正五边形ABCDE内作圆弧,则图中阴影部分图形的面积为 .(结果保留π)
17.如图,在平面直角坐标系中,正六边形OABCDE的边长是2,则它的外接圆圆心P的坐标是 .
18.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
19.如图,正方形ABCD内接于⊙O,点P是上的一点,则∠CPD的度数是 度.
20.如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点,GF=AB=2,∠GCH=60°,则线段EH长 .
21.如图,边长为2的正方形ABCD内接于⊙O,点E是上一点(不与A、B重合),点F是上一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°.有下列结论:①=;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+;④若BG=1﹣,则BG,GE,围成的面积是,其中正确的是 (把所有正确结论的序号都填上)
22.如图,分别以正六边形ABCDEF的顶点A,D为圆心,以AB长为半径画弧BF,弧CE,若AB=1,则阴影部分的面积为 .
23.如图1,将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转 °,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为4,则所得正八边形的面积为 .
24.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则∠MON= 度.
25.如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4∥B3B4,直线l经过B2、B3,则直线l与A1A2的夹角α= °.
26.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于 度.
27.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为 .
28.如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为 .
29.如图,ABCDE是正五边形,已知AG=1,则FG+JH+CD= .
30.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D,E重合),求∠CPD的余角的度数.
31.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
参考答案
1.解:如图,O为正六边形六边形ABCDEF的中心,过O作OH⊥AB于H,连接OA、OB
则OA为正六边形ABCDEF的外接圆的半径,OH为正六边形ABCDEF的边心距,
即OH=,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴∠OAB=60°,
∵OH⊥AB,
∴sin∠OAH=,
∴OA=2,
∴它的外接圆的面积=π 22=4π,
故选:A.
2.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
3.解:如图,连接OB、OC.
∵六边形ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM===2,
故选:A.
4.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
5.解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE=OA=×4=2,
故选:A.
6.解:如图,过点H作FA的延长线的垂线HQ,
∵∠BAF=120°,
∴∠HAQ=60°,∠HQA=90°,
∴∠AHQ=30°,
设AH=x,∴AQ=x,QH=x,
∴BH=B′H=AB﹣AH=6﹣x,
∵AB′=AB=3,
∴B′Q=B′A+AQ=3+x,
在Rt△B′HQ中,根据勾股定理,得
B′H2=B′Q2+QH2,
∴(6﹣x)2=(3+x)2+x2,
解得x=,
∴B′H=6﹣x==,
∵∠HAB′=∠F=∠HB′M=120°,
∴∠AHB′+∠AB′H=60°,∠FB′M+∠AB′H=60°,
∴∠AHB′=∠FB′M,
∴B′M=7,
∴C′M=B′M﹣B′C′=7﹣6=1.
故选:A.
7.解:如图,连接OA、OB,作OG⊥AB于点G,
∵⊙O的周长等于4πcm,
∴⊙O的半径为:=2,
∵ABCDEF是⊙O的内接正六边形,
∴OA=OB=AB=2,
∵OG⊥AB,
∴AG=BG=AB=1,
∴OG=,
∴S△AOB=AB OG
=2×
=.
∴它的内接正六边形ABCDEF的面积是6S△AOB=6(cm2).
故选:C.
8.解:∵五边形的内角和为(5﹣2) 180°=540°,
∴正五边形的每一个内角为540°÷5=108°,
如图,延长正五边形的两边相交于点O,
则∠1=360°﹣108°×3=360°﹣324°=36°,
360°÷36°=10,
∵已经有3个五边形,
∴10﹣3=7,
即完成这一圆环还需7个五边形.
故选:D.
9.解:∵正五边形的每个内角为:=108°,
∴组成的正多边形的每个内角为:360°﹣2×108°﹣24°=120°,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴组成的正多边形为正n边形,
则=120°,
解得:n=6,
故选:B.
10.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
11.解:从O点出发,确定点O分别到A,B,C,D,E的距离,只有OA=OC=OD,
∵三角形的外心到三角形的三个顶点的距离相等,
∴点O是△ACD的外心,
故选:D.
12.解:设DE与⊙O相切于点N,连接OD、OE、ON,作DM⊥OE于M,如图所示:
则ON⊥DE,DE=2,OD=OE,∠DOE==45°,
∵DM⊥OE,
∴△ODM是等腰直角三角形,
∴DM=OM,OE=OD=DM,
设OM=DM=x,则OD=OE=x,EM=OE﹣OM=(﹣1)x,
在Rt△DEM中,由勾股定理得:x2+(﹣1)2x2=22,
解得:x2=2+,
∵△ODE的面积=DE×ON=OE×DM,
∴ON====+1,
即⊙O的半径为:1+;
故选:B.
13.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,=+1.
故选:B.
14.解:连接OA、OB、AB,作OH⊥AB于H,
∵点A、B、C、D、E、F是⊙O的等分点,
∴∠AOB=60°,又OA=OB,
∴△AOB是等边三角形,
∴AB=OB=1,∠ABO=60°,
∴OH==,
∴“三叶轮”图案的面积=(﹣×1×)×6=π﹣,
故选:B.
15.解:设正六边形的中心为O,连接OA,OB.
由题意,OA=OB=AB=4,
∴S弓形AmB=S扇形OAB﹣S△AOB=﹣×42=π﹣4,
∴S阴=6 (S半圆﹣S弓形AmB)=6 ( π 22﹣π+4)=24﹣4π.
故答案为:24﹣4π.
16.解:∵五边形ABCDE是正五边形,
∴∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,
∵AB=2,
∴AB=1,
∴图中阴影部分图形的面积为=π,
故答案为:.
17.解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA==60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH=∠OPA=30°,OH=OA=1,
∴PH===,
∴P的坐标是(1,),
故答案为:(1,).
18.解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
19.解:连接AC,如图,
∵四边形ABCD为正方形,
∴∠CAD=45°,
又∵∠CPD=∠CAD,
∴∠CPD=45°.
故答案是:45.
20.解:如图,作GP∥AB,交BC于点P,AN∥BC交GP于点N,
∴四边形ABPN是平行四边形,
∴PN=AB=6,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠B=∠BCD=∠D=120°,AF=AB=BC=CD=6,
∴∠BAN=∠NAG=∠AGN=60°,∠CPG=∠D=120°,
∴△ANG是等边三角形,
∴NG=AN=AG=6﹣2=4,
∴PG=NG+PN=4+6=10,
∵∠PCG+∠DCH=∠BCD﹣∠GCH=120°﹣60°=60°,
∠DHC+∠DCH=180°﹣∠D=180°﹣120°=60°,
∴∠PCG=∠DHC,
∵∠CPG=∠D,
∵PC=BC﹣BP=6﹣4=2,PG=10,CD=6,
∴DH=,
∴EH=ED﹣DH=6﹣=.
故答案为:.
21.解:如图所示,连接OC、OB、CF、BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴,
∵,
∴;故①正确,
在△BOG与△COH中,,
∴△BOG≌△COH(ASA),
∴OG=OH,BG=CH,
∵∠HOG=90°
∴△OGH是等腰直角三角形,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故②错误;
∵AB=BC,BG=CH,
∴AG=BH,
∴△BGH的周长=BG+BH+GH=BG+AG+OG=AB+OG=2+OG,
当OG⊥AB时,OG的长最小,此时OG=1,
∴△GBH周长的最小值为2+,故③正确;
作OM⊥AB于M,则OM=BM=AB=1,OB=OM=,
∴GM=,
∴∠GOM=30°,
∵∠BOM=45°,
∴∠BOG=45°﹣30°=15°,
∴扇形BOE的面积==,
∵BG=1﹣,
∴AG=1+,
过G作GP⊥BO于P,
∴PG=PB=﹣,
∴△OBG的面积=××( ﹣)=﹣,
∴BG,GE,围成的面积=扇形BOE的面积﹣△BOG的面积=﹣+,故④错误;
故答案为:①③.
22.解:连接OB、OC,
∵六边形ABCDEF是正六边形,
∴∠A=∠D==120°,∠BOC=60°,
∴△OBC为等边三角形,
∴OB=BC=AB=1,
∴阴影部分的面积=×1××6﹣×2
=﹣π,
故答案为:﹣π.
23.解:如图2所示:
将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转,所得图形与原图的重叠部分是正多边形.
在图2中,由题意得:PM=MN=NQ,AM=AP=BN=BQ,
则MN=PM=AM,
∵AM+MN+BN=AB=4,
∴AM+AM+AM=4,
解得:AM=4﹣2,
则所得正八边形的面积为4×4﹣4××(4﹣2)2=32﹣32;
故答案为:(),32﹣32.
24.解:根据正多边形性质得,中心角为:
∠AOB=360°÷9=40°,
∴∠MON=2∠AOB=80°.
故答案为:80.
25.解:设l交A1A2于E、交A4A3于D,如图所示:
∵六边形A1A2A3A4A5A6是正六边形,六边形的内角和=(6﹣2)×180°=720°,
∴∠A1A2A3=∠A2A3A4==120°,
∵五边形B1B2B3B4B5是正五边形,五边形的内角和=(5﹣2)×180°=540°,
∴∠B2B3B4==108°,
∴∠B4B3D=180°﹣108°=72°,
∵A3A4∥B3B4,
∴∠EDA3=∠B4B3D=72°,
∴α=∠A2ED=360°﹣∠A1A2A3﹣∠A2A3A4﹣∠EDA3=360°﹣120°﹣120°﹣72°=48°,
故答案为:48.
26.解:连接OC、OD,如图所示:
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣∠CPD=90°﹣36°=54°,
故答案为:54.
27.解:边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,
所以原来的纸带宽度=×2=.
故答案为:.
28.解:连接OA、OB,作OM⊥AB于M,如图所示:
则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=2,AM=AB=1,
∴OM==,
即正六边形外接圆的半径=2,
它的内切圆的半径=,
所以圆环的面积=π[22﹣()2]=π;
故答案为:π.
29.解:根据对称性可知:GJ∥BH,GB∥JH,
∴四边形JHBG是平行四边形,
∴JH=BG,
同理可证:四边形CDFB是平行四边形,
∴CD=FB,
∴FG+JH+CD=FG+BG+FB=2BF,
设FG=x,
∵∠AFG=∠AFB,∠FAG=∠ABF=36°,
∵AF=AG=BG=1,
∴x(x+1)=1,
∴x=(负根已经舍弃),
∴BF=+1=,
∴FG+JH+CD=+1.
故答案为+1.
30.解:如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∴∠CPD的余角的度数为90°﹣36°=54°.
31.(1)证明:∵六边形ABCDEF为正六边形,
∴每个内角均为120°.
∵∠FMH=120°,A、M、B在一条直线上,
∴∠AFM+∠FMA=∠FMA+∠BMH=60°,
∴∠AFM=∠BMH.
(2)解:猜想:FM=MH.
证明:①当点M与点A重合时,∠FMB=120°,MB与BQ的交点H与点B重合,有FM=MH.
②当点M与点A不重合时,
证法一:如图1,连接FB并延长到G,使BG=BH,连接MG.
∵∠BAF=120°,AF=AB,
∴∠ABF=30°,
∴∠ABG=180°﹣30°=150°.
∵MH与六边形外角的平分线BQ交于点H,
∴∠CBQ=×60°=30°,
∴∠MBH=∠ABC+∠CBQ=120°+30°=150°,
∴∠MBH=∠MBG=150°.
∵,
∴△MBH≌△MBG,
∴∠MHB=∠MGB,MH=MG,
∵∠AFM=∠BMH,∠HMB+∠MHB=30°,
∴∠AFM+∠MGB=30°,
∵∠AFM+∠MFB=30°,
∴∠MFB=∠MGB.
∴FM=MG=MH.
证法二:如图2,在AF上截取FP=MB,连接PM.
∵AF=AB,FP=MB,
∴PA=AM
∵∠A=120°,
∴∠APM=×(180°﹣120°)=30°,
有∠FPM=150°,
∵BQ平分∠CBN,
∴∠MBQ=120°+30°=150°,
∴∠FPM=∠MBH,
由(1)知∠PFM=∠HMB,
∴△FPM≌△MBH.
∴FM=MH.
1.已知一个正六边形的边心距为,则它的外接圆的面积为( )
A.4π B.3π C.2π D.π
2.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
3.如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A. B. C.2 D.
4.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2 B. C.2 D.2
5.正方形外接圆的半径为4,则其内切圆的半径为( )
A.2 B. C.1 D.
6.如图,将边长为6的正六边形ABCDEF沿HG折叠,点B的对应点B′恰好落在边AF的中点上,点C、D的对应点为C′、D′,延长B′C′交EF于点M,则C′M的长为( )
A.1 B.
C. D.
7.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A. B. C. D.
8.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A.10 B.9 C.8 D.7
9.如图,用n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )
A.5 B.6 C.8 D.10
10.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2: B.: C.: D.:2
11.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点.则点O是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
12.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2 B. C.3 D.
13.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则等于( )
A.3 B. C.2 D.
14.如图,点A、B、C、D、E、F是⊙O的等分点,分别以点B、D、F为圆心,AF的长为半径画弧,形成美丽的“三叶轮”图案.已知⊙O的半径为1,那么“三叶轮”图案的面积为( )
A. B. C. D.
15.如图,正六边形的边长为4,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 .
16.如图,在正五边形ABCDE中,AB=2,分别以顶点A、B、C、D、E为圆心,AB的长为半径在正五边形ABCDE内作圆弧,则图中阴影部分图形的面积为 .(结果保留π)
17.如图,在平面直角坐标系中,正六边形OABCDE的边长是2,则它的外接圆圆心P的坐标是 .
18.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
19.如图,正方形ABCD内接于⊙O,点P是上的一点,则∠CPD的度数是 度.
20.如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点,GF=AB=2,∠GCH=60°,则线段EH长 .
21.如图,边长为2的正方形ABCD内接于⊙O,点E是上一点(不与A、B重合),点F是上一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°.有下列结论:①=;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+;④若BG=1﹣,则BG,GE,围成的面积是,其中正确的是 (把所有正确结论的序号都填上)
22.如图,分别以正六边形ABCDEF的顶点A,D为圆心,以AB长为半径画弧BF,弧CE,若AB=1,则阴影部分的面积为 .
23.如图1,将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转 °,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为4,则所得正八边形的面积为 .
24.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则∠MON= 度.
25.如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4∥B3B4,直线l经过B2、B3,则直线l与A1A2的夹角α= °.
26.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于 度.
27.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为 .
28.如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为 .
29.如图,ABCDE是正五边形,已知AG=1,则FG+JH+CD= .
30.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D,E重合),求∠CPD的余角的度数.
31.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
参考答案
1.解:如图,O为正六边形六边形ABCDEF的中心,过O作OH⊥AB于H,连接OA、OB
则OA为正六边形ABCDEF的外接圆的半径,OH为正六边形ABCDEF的边心距,
即OH=,
∵∠AOB==60°,
∴△OAB是等边三角形,
∴∠OAB=60°,
∵OH⊥AB,
∴sin∠OAH=,
∴OA=2,
∴它的外接圆的面积=π 22=4π,
故选:A.
2.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
3.解:如图,连接OB、OC.
∵六边形ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM===2,
故选:A.
4.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
5.解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE=OA=×4=2,
故选:A.
6.解:如图,过点H作FA的延长线的垂线HQ,
∵∠BAF=120°,
∴∠HAQ=60°,∠HQA=90°,
∴∠AHQ=30°,
设AH=x,∴AQ=x,QH=x,
∴BH=B′H=AB﹣AH=6﹣x,
∵AB′=AB=3,
∴B′Q=B′A+AQ=3+x,
在Rt△B′HQ中,根据勾股定理,得
B′H2=B′Q2+QH2,
∴(6﹣x)2=(3+x)2+x2,
解得x=,
∴B′H=6﹣x==,
∵∠HAB′=∠F=∠HB′M=120°,
∴∠AHB′+∠AB′H=60°,∠FB′M+∠AB′H=60°,
∴∠AHB′=∠FB′M,
∴B′M=7,
∴C′M=B′M﹣B′C′=7﹣6=1.
故选:A.
7.解:如图,连接OA、OB,作OG⊥AB于点G,
∵⊙O的周长等于4πcm,
∴⊙O的半径为:=2,
∵ABCDEF是⊙O的内接正六边形,
∴OA=OB=AB=2,
∵OG⊥AB,
∴AG=BG=AB=1,
∴OG=,
∴S△AOB=AB OG
=2×
=.
∴它的内接正六边形ABCDEF的面积是6S△AOB=6(cm2).
故选:C.
8.解:∵五边形的内角和为(5﹣2) 180°=540°,
∴正五边形的每一个内角为540°÷5=108°,
如图,延长正五边形的两边相交于点O,
则∠1=360°﹣108°×3=360°﹣324°=36°,
360°÷36°=10,
∵已经有3个五边形,
∴10﹣3=7,
即完成这一圆环还需7个五边形.
故选:D.
9.解:∵正五边形的每个内角为:=108°,
∴组成的正多边形的每个内角为:360°﹣2×108°﹣24°=120°,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴组成的正多边形为正n边形,
则=120°,
解得:n=6,
故选:B.
10.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
11.解:从O点出发,确定点O分别到A,B,C,D,E的距离,只有OA=OC=OD,
∵三角形的外心到三角形的三个顶点的距离相等,
∴点O是△ACD的外心,
故选:D.
12.解:设DE与⊙O相切于点N,连接OD、OE、ON,作DM⊥OE于M,如图所示:
则ON⊥DE,DE=2,OD=OE,∠DOE==45°,
∵DM⊥OE,
∴△ODM是等腰直角三角形,
∴DM=OM,OE=OD=DM,
设OM=DM=x,则OD=OE=x,EM=OE﹣OM=(﹣1)x,
在Rt△DEM中,由勾股定理得:x2+(﹣1)2x2=22,
解得:x2=2+,
∵△ODE的面积=DE×ON=OE×DM,
∴ON====+1,
即⊙O的半径为:1+;
故选:B.
13.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,=+1.
故选:B.
14.解:连接OA、OB、AB,作OH⊥AB于H,
∵点A、B、C、D、E、F是⊙O的等分点,
∴∠AOB=60°,又OA=OB,
∴△AOB是等边三角形,
∴AB=OB=1,∠ABO=60°,
∴OH==,
∴“三叶轮”图案的面积=(﹣×1×)×6=π﹣,
故选:B.
15.解:设正六边形的中心为O,连接OA,OB.
由题意,OA=OB=AB=4,
∴S弓形AmB=S扇形OAB﹣S△AOB=﹣×42=π﹣4,
∴S阴=6 (S半圆﹣S弓形AmB)=6 ( π 22﹣π+4)=24﹣4π.
故答案为:24﹣4π.
16.解:∵五边形ABCDE是正五边形,
∴∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,
∵AB=2,
∴AB=1,
∴图中阴影部分图形的面积为=π,
故答案为:.
17.解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA==60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH=∠OPA=30°,OH=OA=1,
∴PH===,
∴P的坐标是(1,),
故答案为:(1,).
18.解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
19.解:连接AC,如图,
∵四边形ABCD为正方形,
∴∠CAD=45°,
又∵∠CPD=∠CAD,
∴∠CPD=45°.
故答案是:45.
20.解:如图,作GP∥AB,交BC于点P,AN∥BC交GP于点N,
∴四边形ABPN是平行四边形,
∴PN=AB=6,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠B=∠BCD=∠D=120°,AF=AB=BC=CD=6,
∴∠BAN=∠NAG=∠AGN=60°,∠CPG=∠D=120°,
∴△ANG是等边三角形,
∴NG=AN=AG=6﹣2=4,
∴PG=NG+PN=4+6=10,
∵∠PCG+∠DCH=∠BCD﹣∠GCH=120°﹣60°=60°,
∠DHC+∠DCH=180°﹣∠D=180°﹣120°=60°,
∴∠PCG=∠DHC,
∵∠CPG=∠D,
∵PC=BC﹣BP=6﹣4=2,PG=10,CD=6,
∴DH=,
∴EH=ED﹣DH=6﹣=.
故答案为:.
21.解:如图所示,连接OC、OB、CF、BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴,
∵,
∴;故①正确,
在△BOG与△COH中,,
∴△BOG≌△COH(ASA),
∴OG=OH,BG=CH,
∵∠HOG=90°
∴△OGH是等腰直角三角形,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故②错误;
∵AB=BC,BG=CH,
∴AG=BH,
∴△BGH的周长=BG+BH+GH=BG+AG+OG=AB+OG=2+OG,
当OG⊥AB时,OG的长最小,此时OG=1,
∴△GBH周长的最小值为2+,故③正确;
作OM⊥AB于M,则OM=BM=AB=1,OB=OM=,
∴GM=,
∴∠GOM=30°,
∵∠BOM=45°,
∴∠BOG=45°﹣30°=15°,
∴扇形BOE的面积==,
∵BG=1﹣,
∴AG=1+,
过G作GP⊥BO于P,
∴PG=PB=﹣,
∴△OBG的面积=××( ﹣)=﹣,
∴BG,GE,围成的面积=扇形BOE的面积﹣△BOG的面积=﹣+,故④错误;
故答案为:①③.
22.解:连接OB、OC,
∵六边形ABCDEF是正六边形,
∴∠A=∠D==120°,∠BOC=60°,
∴△OBC为等边三角形,
∴OB=BC=AB=1,
∴阴影部分的面积=×1××6﹣×2
=﹣π,
故答案为:﹣π.
23.解:如图2所示:
将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转,所得图形与原图的重叠部分是正多边形.
在图2中,由题意得:PM=MN=NQ,AM=AP=BN=BQ,
则MN=PM=AM,
∵AM+MN+BN=AB=4,
∴AM+AM+AM=4,
解得:AM=4﹣2,
则所得正八边形的面积为4×4﹣4××(4﹣2)2=32﹣32;
故答案为:(),32﹣32.
24.解:根据正多边形性质得,中心角为:
∠AOB=360°÷9=40°,
∴∠MON=2∠AOB=80°.
故答案为:80.
25.解:设l交A1A2于E、交A4A3于D,如图所示:
∵六边形A1A2A3A4A5A6是正六边形,六边形的内角和=(6﹣2)×180°=720°,
∴∠A1A2A3=∠A2A3A4==120°,
∵五边形B1B2B3B4B5是正五边形,五边形的内角和=(5﹣2)×180°=540°,
∴∠B2B3B4==108°,
∴∠B4B3D=180°﹣108°=72°,
∵A3A4∥B3B4,
∴∠EDA3=∠B4B3D=72°,
∴α=∠A2ED=360°﹣∠A1A2A3﹣∠A2A3A4﹣∠EDA3=360°﹣120°﹣120°﹣72°=48°,
故答案为:48.
26.解:连接OC、OD,如图所示:
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣∠CPD=90°﹣36°=54°,
故答案为:54.
27.解:边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,
所以原来的纸带宽度=×2=.
故答案为:.
28.解:连接OA、OB,作OM⊥AB于M,如图所示:
则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=2,AM=AB=1,
∴OM==,
即正六边形外接圆的半径=2,
它的内切圆的半径=,
所以圆环的面积=π[22﹣()2]=π;
故答案为:π.
29.解:根据对称性可知:GJ∥BH,GB∥JH,
∴四边形JHBG是平行四边形,
∴JH=BG,
同理可证:四边形CDFB是平行四边形,
∴CD=FB,
∴FG+JH+CD=FG+BG+FB=2BF,
设FG=x,
∵∠AFG=∠AFB,∠FAG=∠ABF=36°,
∵AF=AG=BG=1,
∴x(x+1)=1,
∴x=(负根已经舍弃),
∴BF=+1=,
∴FG+JH+CD=+1.
故答案为+1.
30.解:如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∴∠CPD的余角的度数为90°﹣36°=54°.
31.(1)证明:∵六边形ABCDEF为正六边形,
∴每个内角均为120°.
∵∠FMH=120°,A、M、B在一条直线上,
∴∠AFM+∠FMA=∠FMA+∠BMH=60°,
∴∠AFM=∠BMH.
(2)解:猜想:FM=MH.
证明:①当点M与点A重合时,∠FMB=120°,MB与BQ的交点H与点B重合,有FM=MH.
②当点M与点A不重合时,
证法一:如图1,连接FB并延长到G,使BG=BH,连接MG.
∵∠BAF=120°,AF=AB,
∴∠ABF=30°,
∴∠ABG=180°﹣30°=150°.
∵MH与六边形外角的平分线BQ交于点H,
∴∠CBQ=×60°=30°,
∴∠MBH=∠ABC+∠CBQ=120°+30°=150°,
∴∠MBH=∠MBG=150°.
∵,
∴△MBH≌△MBG,
∴∠MHB=∠MGB,MH=MG,
∵∠AFM=∠BMH,∠HMB+∠MHB=30°,
∴∠AFM+∠MGB=30°,
∵∠AFM+∠MFB=30°,
∴∠MFB=∠MGB.
∴FM=MG=MH.
证法二:如图2,在AF上截取FP=MB,连接PM.
∵AF=AB,FP=MB,
∴PA=AM
∵∠A=120°,
∴∠APM=×(180°﹣120°)=30°,
有∠FPM=150°,
∵BQ平分∠CBN,
∴∠MBQ=120°+30°=150°,
∴∠FPM=∠MBH,
由(1)知∠PFM=∠HMB,
∴△FPM≌△MBH.
∴FM=MH.
同课章节目录
