《3.8弧长及扇形面积》同步练习 2021-2022学年浙教版九年级数学上册(Word版含解析)
文档属性
| 名称 | 《3.8弧长及扇形面积》同步练习 2021-2022学年浙教版九年级数学上册(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 482.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《3.8弧长及扇形面积》同步练习题(附答案)
1.如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( )
A.2π B. C. D.
2.如图,四边形ABCD是一个矩形,⊙C的半径是2cm,CF=4cm,EF=2cm.则图中阴影部分的面积约为(精确到0.1cm2)( )
A.4.0cm2 B.4.1cm2 C.4.19cm2 D.4.2cm2
3.如图,BC为⊙O直径,若∠A=80°,BC=6,则图中灰色区域的面积为( )
A.2π B.3π C.4π D.5π
4.如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( )
A.P>Q B.P<Q C.P=Q D.无法确定
5.如图,在扇形AOB中,∠AOB=90°,OA=2,点C、D分别为OA、OB的中点,分别以C、D为圆心,以OA、OB为直径作半圆,两半圆交于点E,则阴影部分的面积为( )
A. B. C. D.
6.如图,⊙O1与⊙O2的半径均为5,⊙O1的两条弦长分别为6和8,⊙O2的两条弦长均为7,则图中阴影部分面积的大小关系为( )
A.S1>S2 B.S1<S2 C.S1=S2 D.无法确定
7.如图,在直角扇形ABC内,分别以AB和AC为直径作半圆,两条半圆弧相交于点D,整个图形被分成S1,S2,S3,S4四部分,则S2和S4的大小关系是( )
A.S2<S4 B.S2=S4 C.S2>S4 D.无法确定
8.如图,矩形ABCD中.AB=3,BC=6,以点B为圆心、BA为半径画弧,交BC于点E,以点D为圆心、DA为半径画弧,交BC于点F,则阴影部分的面积为( )
A. B.6π﹣ C. D.
9.已知扇形的圆心角为135°,半径为3,则此扇形的面积是 (结果保留π)
10.如图,扇形AOB的圆心角为直角,边长为1的正方形ODCF的顶点F,D,C分别在OA,OB,上,过点B作BE⊥FC,交FC的延长线于点E,则图中阴影部分的面积等于 .
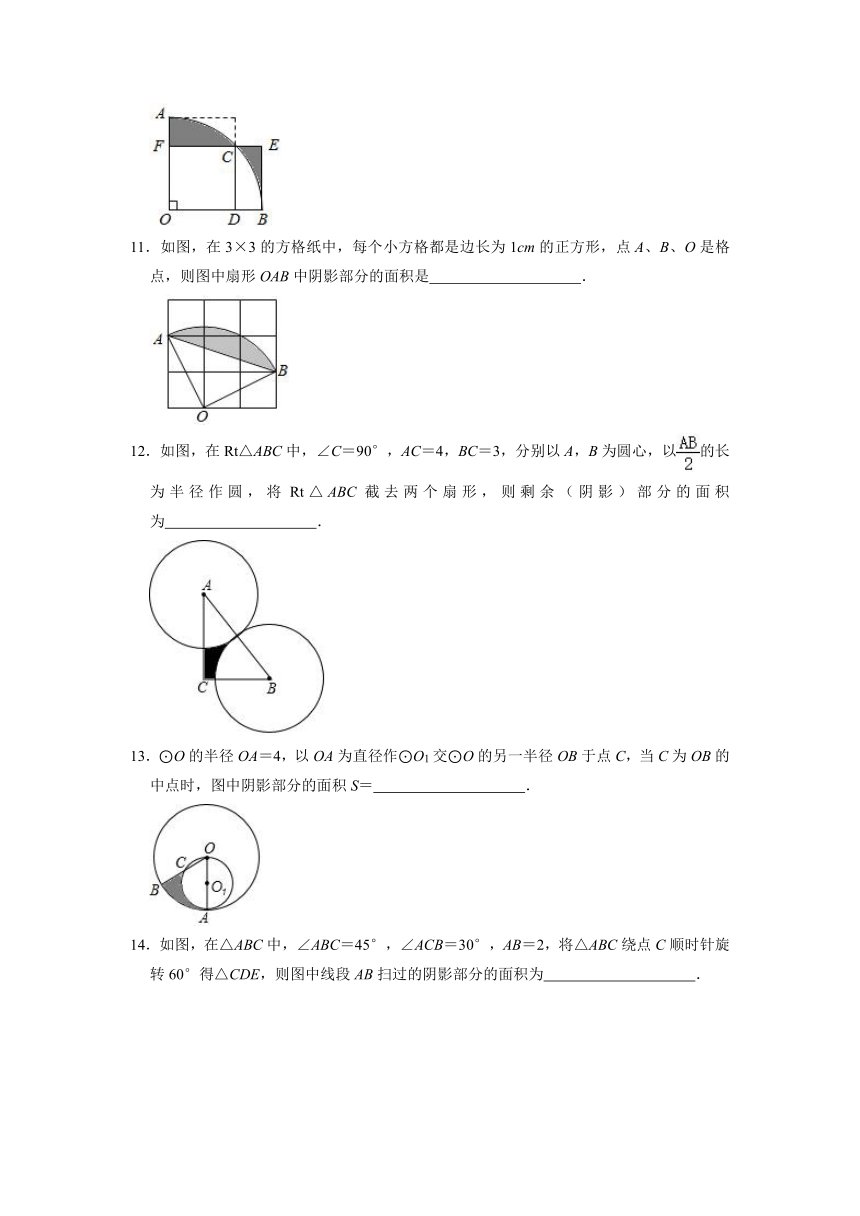
11.如图,在3×3的方格纸中,每个小方格都是边长为1cm的正方形,点A、B、O是格点,则图中扇形OAB中阴影部分的面积是 .
12.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以A,B为圆心,以的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为 .
13.⊙O的半径OA=4,以OA为直径作⊙O1交⊙O的另一半径OB于点C,当C为OB的中点时,图中阴影部分的面积S= .
14.如图,在△ABC中,∠ABC=45°,∠ACB=30°,AB=2,将△ABC绕点C顺时针旋转60°得△CDE,则图中线段AB扫过的阴影部分的面积为 .
15.如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=6,则阴影部分的面积为 .
16.如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=6,则图中阴影部分的面积为 .
17.如图,E是正方形ABCD内一点,连接EA、EB并将△BAE以B为中心顺时针旋转90°得到△BFC,若
BA=4,BE=3,在△BAE旋转到△BCF的过程中AE扫过区域面积 .
18.如图,在圆心角为90°的扇形OAB中,半径OA=cm,C为的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2.
19.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为 .(结果保留π)
20.如图,三个圆心相同的圆心角∠AOB=120°,半径OA=6cm,C、D是的三等分点,则阴影部分的面积之和为 cm2(结果保留π).
21.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4,则阴影部分图形的面积为 .
22.如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°
(1)求证:BD=CD;
(2)若圆O的半径为3,求的长.
23.如图所示,∠AOB=90°,∠COB=45°,
(1)已知OB=10,求以OB为直径的半圆面积及扇形COB的面积;(结果可保留π)
(2)填空:已知阴影甲的面积为6平方厘米,则阴影乙的面积为 平方厘米.
24.如图所示,已知甲、乙、丙三种图案的地砖,它们都是边长为4的正方形.
①甲地砖以正方形的边长为半径作弧得到甲图所示的阴影部分;
②乙地砖以正方形的边长为直径作弧得到乙图所示的阴影部分;
③丙地砖以正方形边长的一半为直径作弧得到丙图所示的阴影部分;
设三种地砖的阴影部分面积分别为S甲、S乙和S丙.
(1)请你直接写出S甲= .(结果保留π)
(2)请你直接将S甲和S乙的数量关系填在横线上: .
(3)由题(2)中面积的数量关系,可直接求得S丙= .(结果保留π)
25.如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和.
26.如图,半圆的直径AB=40,C,D是半圆的三等分点,求弦AC,AD与围成的阴影部分的面积.
27.已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)在(2)的条件下,求图中阴影部分的面积.
28.如图,已知扇形AOB的圆心角为直角,正方形OCDE内接于扇形AOB.点C、E、D分别在OA、OB、弧AB上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和.
参考答案
1.解:如图,连接CO,
∵∠BAC=50°,AO=CO=3,
∴∠ACO=50°,
∴∠AOC=80°,
∴劣弧AC的长为=,
故选:D.
2.解:∵在Rt△CEF中,CF=4,EF=2,
∴∠C=30°,
又∵∠BCD=90°,⊙C的半径是2,
∴阴影部分面积为=≈4.2cm2.
故选:D.
3.解:∵∠A=80°,
∴∠B+∠C=180°﹣80°=100°,
∵OB=OD,OE=OC,
∴∠ODB=∠B,∠OEC=∠C,
∴∠ODB+∠OEC=100°,
∴∠DOB+∠EOC=160°,
∴图中灰色区域的面积==4π,故选:C.
4.解:设OA=a,
扇形OAB的面积==,
以OA,OB为直径在扇形内作的半圆的面积=×π×()2=,
P=扇形OAB的面积﹣(以OA为直径的半圆的面积+以OB为直径的半圆的面积)+Q=﹣×2+Q=Q
故选:C.
5.解:连接OE、DE,
由题意得,∠EOD=45°,
∵DO=DE,
∴∠ODE=90°,
∴弓形OGE的面积=﹣×1×1=﹣,
∴阴影部分的面积=﹣×π×12×2+(﹣)×2=﹣1,
故选:B.
6.解:通过旋转,拼接得到下面图形.
∵62+82=102,
∴△ABC是直角三角形,S△ABC=24,
右边图中,DE=EF=7,作O2M⊥DE,连接O2E交DF于H.
∴EH=4.9,DF=2DH=2=2≈10,
∴S△DEF=>S△ABC,
∵左边空白部分面积=半圆面积﹣S△ABC,右边空白部分面积=弓形DEF的面积﹣△DEF的面积,半圆面积>弓形DEF的面积,
∴左边的空白部分面积>右边空白部分面积,
∴S2>S1,
故选:B.
7.解:设AB=AC=2a,根据题意得,
S2=S扇形ACB﹣S半圆AB﹣S半圆AC+S4=﹣2××π×a2+S4=S4,
所以S2=S4.
故选:B.
8.解:如图,连接DF.
∵四边形ABCD是矩形,
∴∠B=∠C=∠ADC=90°,AB=CD=3,AD=DF=BC=6,
∴CF==3,BF=BC﹣CF=3,
∴∠FDC=30°,∠ADF=60°
∴S阴=S扇形ABE﹣(S矩形ABCD﹣S扇形DAF﹣S△DCF)
=﹣(18﹣﹣ 3 3)
=π﹣,
故选:A.
9.解:扇形的面积==,
故答案为:.
10.解:连接OC,
∵正方形的边长为1,即OD=CD=1,
∴OC==,
∴BD=OB﹣OD=﹣1,
∵OA=OB,OF=OD,
∴AF=BD,
∵CF=CD,
∴阴影部分的面积=长方形CDBE的面积=﹣1,
故答案为:﹣1.
11.解∵∠ACO=90°,
∴∠CAO+∠AOC=90°,
在△ACO和△ODB中,
,
∴△ACO≌△ODB(SAS),
∴∠CAO=∠BOD,
∴∠BOD+∠AOC=90°,
∴∠AOB=90°,
由勾股定理得,OA=OB==(cm),
∴扇形OAB中阴影部分的面积=﹣××=(﹣)cm2,
故答案为:(﹣)cm2.
12.解:∵Rt△ABC中,∠ABC=90°,AC=4,BC=3,
∴AB==5,
∴S阴影部分=×3×4﹣=6﹣π.
故答案是:6﹣π.
13.解:连接O1C,
∵C是OB的中点,OA=OB=4,
∴OC=2,
∵O1是OA的中点,
∴O1A=O1O=2,
∴OC=O1O=O1C=2,
∴△OO1C是等边三角形,
∴∠AOB=∠OO1C=60°,
∴∠AO1C=120°,
∴S阴影=﹣﹣=﹣.
故答案为:.
14.解:作AF⊥BC于F,
∵∠ABC=45°,
∴AF=BF=AB=,
在Rt△AFC中,∠ACB=30°,
∴AC=2AF=2,FC=,
由旋转的性质可知,S△ABC=S△EDC,
∴图中线段AB扫过的阴影部分的面积=扇形DCB的面积+△EDC的面积﹣△ABC的面积﹣扇形ACE的面积
=扇形DCB的面积﹣扇形ACE的面积
=﹣
=,
故答案为:.
15.解:连接OC、AC,
∵OA=OC=AC,
∴△AOC为等边三角形,
∴∠OAC=60°,S△OAC=×6×6×=9,
∴∠BOC=30°,
S扇形OAC==6π,
则阴影部分的面积=﹣(6π﹣9)=9﹣3π,
故答案为:9﹣3π.
16.解:连接OC、OD、AC,
∵点C,D是半圆O的三等分点,
∴CD∥AB,∠COD=60°,
∵OC=OD,
∴△ODC是等边三角形.
∵CD∥AB,
∴△ACD面积等于△OCD面积.
所以阴影部分面积等于扇形COD面积==6π.
故答案为6π.
17.解:∵△BAE以B为中心顺时针旋转90°得到△BFC,
∴△BAE≌△BFC
∴阴影部分的面积=S扇形BAC﹣S扇形BEF=﹣==,
故答案为:π.
18.解:连接OC,过C点作CF⊥OA于F,
∵半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF=1,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积=﹣×1×=π﹣(cm2)
三角形ODE的面积=OD×OE=××=(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积=﹣( π﹣)﹣=π﹣π+﹣=π+﹣.
故答案为:π+﹣.
19.解:∵四边形ABCD是正方形,
∴∠DCB=90°,DC=AB=4cm.
扇形BAC与扇形CBD的弧交于点E,
∴△BCE是等边三角形,∠ECB=60°,
∴∠DCE=∠DCB﹣∠ECB=30°.
根据图形的割补,可得阴影的面积是扇形DCE,
S扇形DCE=π×42×=πcm2.
故答案为:πcm2.
20.解:扇形面积公式==4πcm2.
21.解:如图,假设线段CD、AB交于点E,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2,
又∵∠CDB=30°,
∴∠COE=2∠CDB=60°,∠OCE=30°,
∴OE=2,OC=2OE=4,
∴S阴影=S扇形OCB﹣S△COE+S△BED=﹣OE×EC+BE ED=﹣2+2=.
故答案为:.
22.(1)证明:∵四边形ABCD内接于圆O,
∴∠C=180°﹣∠BAD=75°,
∵∠DBC=75°,
∴∠DBC=∠C,
∴DB=DC;
(2)解:连接OB、OC,
∵∠DBC=∠C=75°,
∴∠BDC=30°,
由圆周角定理得,∠BOC=2∠BDC=60°,
∴的长==π.
23.解:(1)根据题意得:
S半圆=,
S扇=;
(2)观察图形可知:
阴影甲的面积=阴影乙的面积=6平方厘米,
故答案为:6.
24.解:(1)S甲=2(π×42﹣4×4)
=8π﹣16;
故答案为:8π﹣16;
(2)∵S乙=4[π×()2﹣()×()]
=4π﹣8,
故答案为:S甲=2S乙;
(3)S丙=16[π×()2﹣()×()]
=4π﹣8.
故答案为:4π﹣8.
25.解:如图,作直径MN,使MN⊥EF于O,交AB于G,交CD于H;连接OA、OB、OC、OD;
在Rt△OBG中,BG=3cm,OB=5cm,因此OG=4cm;
同理:在Rt△OCH中,CH=4cm,OC=5cm,因此OH=3cm;
即∠DOF=∠AOM=∠COE=∠BOM,∠CON=∠DON=∠AOE=∠BOF,
因此S扇形OAE=S扇形OBF=S扇形CON=S扇形ODN
∴S阴影=S△ABE+S弓形AMB+S△CDF+S弓形CND
=S△OAB+S弓形AMB+S△OCD+S弓形CND
=S扇形OAB+S扇形OCN+S扇形ODN
=S扇形OAB+S扇形OAE+S扇形OBF
=S⊙O
=12.5πcm2.
故图中阴影部分面积之和为12.5πcm2.
26.解:连接OC、OD、CD.
∵△COD和△CDA等底等高,
∴S△COD=S△ACD.
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
∴阴影部分的面积=S扇形COD==π.
27.证明:(1)连接DO.
∵△ABC是等边三角形,
∴∠A=∠C=60°.
∵OA=OD,
∴△OAD是等边三角形.
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°﹣∠C=30°,
∴∠FDO=180°﹣∠ADO﹣∠CDF=90°,
∴DF为⊙O的切线;
(2)∵△OAD是等边三角形,
∴AD=AO=AB=2.
∴CD=AC﹣AD=2.
Rt△CDF中,
∵∠CDF=30°,
∴CF=CD=1.
∴DF=;
(3)连接OE,由(2)同理可知CE=2.
∴CF=1,
∴EF=1.
∴S直角梯形FDOE=(EF+OD) DF=,
∴S扇形OED==,
∴S阴影=S直角梯形FDOE﹣S扇形OED=﹣.
28.解:连接OD,
∵正方形的边长为1,即OC=CD=1,
∴OD=,
∴AC=OA﹣OC=﹣1,
∵DE=DC,BE=AC,弧BD=弧AD
∴S阴=长方形ACDF的面积=AC CD=﹣1.
1.如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( )
A.2π B. C. D.
2.如图,四边形ABCD是一个矩形,⊙C的半径是2cm,CF=4cm,EF=2cm.则图中阴影部分的面积约为(精确到0.1cm2)( )
A.4.0cm2 B.4.1cm2 C.4.19cm2 D.4.2cm2
3.如图,BC为⊙O直径,若∠A=80°,BC=6,则图中灰色区域的面积为( )
A.2π B.3π C.4π D.5π
4.如图,扇形OAB的圆心角为90°,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是( )
A.P>Q B.P<Q C.P=Q D.无法确定
5.如图,在扇形AOB中,∠AOB=90°,OA=2,点C、D分别为OA、OB的中点,分别以C、D为圆心,以OA、OB为直径作半圆,两半圆交于点E,则阴影部分的面积为( )
A. B. C. D.
6.如图,⊙O1与⊙O2的半径均为5,⊙O1的两条弦长分别为6和8,⊙O2的两条弦长均为7,则图中阴影部分面积的大小关系为( )
A.S1>S2 B.S1<S2 C.S1=S2 D.无法确定
7.如图,在直角扇形ABC内,分别以AB和AC为直径作半圆,两条半圆弧相交于点D,整个图形被分成S1,S2,S3,S4四部分,则S2和S4的大小关系是( )
A.S2<S4 B.S2=S4 C.S2>S4 D.无法确定
8.如图,矩形ABCD中.AB=3,BC=6,以点B为圆心、BA为半径画弧,交BC于点E,以点D为圆心、DA为半径画弧,交BC于点F,则阴影部分的面积为( )
A. B.6π﹣ C. D.
9.已知扇形的圆心角为135°,半径为3,则此扇形的面积是 (结果保留π)
10.如图,扇形AOB的圆心角为直角,边长为1的正方形ODCF的顶点F,D,C分别在OA,OB,上,过点B作BE⊥FC,交FC的延长线于点E,则图中阴影部分的面积等于 .
11.如图,在3×3的方格纸中,每个小方格都是边长为1cm的正方形,点A、B、O是格点,则图中扇形OAB中阴影部分的面积是 .
12.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以A,B为圆心,以的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为 .
13.⊙O的半径OA=4,以OA为直径作⊙O1交⊙O的另一半径OB于点C,当C为OB的中点时,图中阴影部分的面积S= .
14.如图,在△ABC中,∠ABC=45°,∠ACB=30°,AB=2,将△ABC绕点C顺时针旋转60°得△CDE,则图中线段AB扫过的阴影部分的面积为 .
15.如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=6,则阴影部分的面积为 .
16.如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=6,则图中阴影部分的面积为 .
17.如图,E是正方形ABCD内一点,连接EA、EB并将△BAE以B为中心顺时针旋转90°得到△BFC,若
BA=4,BE=3,在△BAE旋转到△BCF的过程中AE扫过区域面积 .
18.如图,在圆心角为90°的扇形OAB中,半径OA=cm,C为的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2.
19.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为 .(结果保留π)
20.如图,三个圆心相同的圆心角∠AOB=120°,半径OA=6cm,C、D是的三等分点,则阴影部分的面积之和为 cm2(结果保留π).
21.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4,则阴影部分图形的面积为 .
22.如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°
(1)求证:BD=CD;
(2)若圆O的半径为3,求的长.
23.如图所示,∠AOB=90°,∠COB=45°,
(1)已知OB=10,求以OB为直径的半圆面积及扇形COB的面积;(结果可保留π)
(2)填空:已知阴影甲的面积为6平方厘米,则阴影乙的面积为 平方厘米.
24.如图所示,已知甲、乙、丙三种图案的地砖,它们都是边长为4的正方形.
①甲地砖以正方形的边长为半径作弧得到甲图所示的阴影部分;
②乙地砖以正方形的边长为直径作弧得到乙图所示的阴影部分;
③丙地砖以正方形边长的一半为直径作弧得到丙图所示的阴影部分;
设三种地砖的阴影部分面积分别为S甲、S乙和S丙.
(1)请你直接写出S甲= .(结果保留π)
(2)请你直接将S甲和S乙的数量关系填在横线上: .
(3)由题(2)中面积的数量关系,可直接求得S丙= .(结果保留π)
25.如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和.
26.如图,半圆的直径AB=40,C,D是半圆的三等分点,求弦AC,AD与围成的阴影部分的面积.
27.已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)在(2)的条件下,求图中阴影部分的面积.
28.如图,已知扇形AOB的圆心角为直角,正方形OCDE内接于扇形AOB.点C、E、D分别在OA、OB、弧AB上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和.
参考答案
1.解:如图,连接CO,
∵∠BAC=50°,AO=CO=3,
∴∠ACO=50°,
∴∠AOC=80°,
∴劣弧AC的长为=,
故选:D.
2.解:∵在Rt△CEF中,CF=4,EF=2,
∴∠C=30°,
又∵∠BCD=90°,⊙C的半径是2,
∴阴影部分面积为=≈4.2cm2.
故选:D.
3.解:∵∠A=80°,
∴∠B+∠C=180°﹣80°=100°,
∵OB=OD,OE=OC,
∴∠ODB=∠B,∠OEC=∠C,
∴∠ODB+∠OEC=100°,
∴∠DOB+∠EOC=160°,
∴图中灰色区域的面积==4π,故选:C.
4.解:设OA=a,
扇形OAB的面积==,
以OA,OB为直径在扇形内作的半圆的面积=×π×()2=,
P=扇形OAB的面积﹣(以OA为直径的半圆的面积+以OB为直径的半圆的面积)+Q=﹣×2+Q=Q
故选:C.
5.解:连接OE、DE,
由题意得,∠EOD=45°,
∵DO=DE,
∴∠ODE=90°,
∴弓形OGE的面积=﹣×1×1=﹣,
∴阴影部分的面积=﹣×π×12×2+(﹣)×2=﹣1,
故选:B.
6.解:通过旋转,拼接得到下面图形.
∵62+82=102,
∴△ABC是直角三角形,S△ABC=24,
右边图中,DE=EF=7,作O2M⊥DE,连接O2E交DF于H.
∴EH=4.9,DF=2DH=2=2≈10,
∴S△DEF=>S△ABC,
∵左边空白部分面积=半圆面积﹣S△ABC,右边空白部分面积=弓形DEF的面积﹣△DEF的面积,半圆面积>弓形DEF的面积,
∴左边的空白部分面积>右边空白部分面积,
∴S2>S1,
故选:B.
7.解:设AB=AC=2a,根据题意得,
S2=S扇形ACB﹣S半圆AB﹣S半圆AC+S4=﹣2××π×a2+S4=S4,
所以S2=S4.
故选:B.
8.解:如图,连接DF.
∵四边形ABCD是矩形,
∴∠B=∠C=∠ADC=90°,AB=CD=3,AD=DF=BC=6,
∴CF==3,BF=BC﹣CF=3,
∴∠FDC=30°,∠ADF=60°
∴S阴=S扇形ABE﹣(S矩形ABCD﹣S扇形DAF﹣S△DCF)
=﹣(18﹣﹣ 3 3)
=π﹣,
故选:A.
9.解:扇形的面积==,
故答案为:.
10.解:连接OC,
∵正方形的边长为1,即OD=CD=1,
∴OC==,
∴BD=OB﹣OD=﹣1,
∵OA=OB,OF=OD,
∴AF=BD,
∵CF=CD,
∴阴影部分的面积=长方形CDBE的面积=﹣1,
故答案为:﹣1.
11.解∵∠ACO=90°,
∴∠CAO+∠AOC=90°,
在△ACO和△ODB中,
,
∴△ACO≌△ODB(SAS),
∴∠CAO=∠BOD,
∴∠BOD+∠AOC=90°,
∴∠AOB=90°,
由勾股定理得,OA=OB==(cm),
∴扇形OAB中阴影部分的面积=﹣××=(﹣)cm2,
故答案为:(﹣)cm2.
12.解:∵Rt△ABC中,∠ABC=90°,AC=4,BC=3,
∴AB==5,
∴S阴影部分=×3×4﹣=6﹣π.
故答案是:6﹣π.
13.解:连接O1C,
∵C是OB的中点,OA=OB=4,
∴OC=2,
∵O1是OA的中点,
∴O1A=O1O=2,
∴OC=O1O=O1C=2,
∴△OO1C是等边三角形,
∴∠AOB=∠OO1C=60°,
∴∠AO1C=120°,
∴S阴影=﹣﹣=﹣.
故答案为:.
14.解:作AF⊥BC于F,
∵∠ABC=45°,
∴AF=BF=AB=,
在Rt△AFC中,∠ACB=30°,
∴AC=2AF=2,FC=,
由旋转的性质可知,S△ABC=S△EDC,
∴图中线段AB扫过的阴影部分的面积=扇形DCB的面积+△EDC的面积﹣△ABC的面积﹣扇形ACE的面积
=扇形DCB的面积﹣扇形ACE的面积
=﹣
=,
故答案为:.
15.解:连接OC、AC,
∵OA=OC=AC,
∴△AOC为等边三角形,
∴∠OAC=60°,S△OAC=×6×6×=9,
∴∠BOC=30°,
S扇形OAC==6π,
则阴影部分的面积=﹣(6π﹣9)=9﹣3π,
故答案为:9﹣3π.
16.解:连接OC、OD、AC,
∵点C,D是半圆O的三等分点,
∴CD∥AB,∠COD=60°,
∵OC=OD,
∴△ODC是等边三角形.
∵CD∥AB,
∴△ACD面积等于△OCD面积.
所以阴影部分面积等于扇形COD面积==6π.
故答案为6π.
17.解:∵△BAE以B为中心顺时针旋转90°得到△BFC,
∴△BAE≌△BFC
∴阴影部分的面积=S扇形BAC﹣S扇形BEF=﹣==,
故答案为:π.
18.解:连接OC,过C点作CF⊥OA于F,
∵半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF=1,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积=﹣×1×=π﹣(cm2)
三角形ODE的面积=OD×OE=××=(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积=﹣( π﹣)﹣=π﹣π+﹣=π+﹣.
故答案为:π+﹣.
19.解:∵四边形ABCD是正方形,
∴∠DCB=90°,DC=AB=4cm.
扇形BAC与扇形CBD的弧交于点E,
∴△BCE是等边三角形,∠ECB=60°,
∴∠DCE=∠DCB﹣∠ECB=30°.
根据图形的割补,可得阴影的面积是扇形DCE,
S扇形DCE=π×42×=πcm2.
故答案为:πcm2.
20.解:扇形面积公式==4πcm2.
21.解:如图,假设线段CD、AB交于点E,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2,
又∵∠CDB=30°,
∴∠COE=2∠CDB=60°,∠OCE=30°,
∴OE=2,OC=2OE=4,
∴S阴影=S扇形OCB﹣S△COE+S△BED=﹣OE×EC+BE ED=﹣2+2=.
故答案为:.
22.(1)证明:∵四边形ABCD内接于圆O,
∴∠C=180°﹣∠BAD=75°,
∵∠DBC=75°,
∴∠DBC=∠C,
∴DB=DC;
(2)解:连接OB、OC,
∵∠DBC=∠C=75°,
∴∠BDC=30°,
由圆周角定理得,∠BOC=2∠BDC=60°,
∴的长==π.
23.解:(1)根据题意得:
S半圆=,
S扇=;
(2)观察图形可知:
阴影甲的面积=阴影乙的面积=6平方厘米,
故答案为:6.
24.解:(1)S甲=2(π×42﹣4×4)
=8π﹣16;
故答案为:8π﹣16;
(2)∵S乙=4[π×()2﹣()×()]
=4π﹣8,
故答案为:S甲=2S乙;
(3)S丙=16[π×()2﹣()×()]
=4π﹣8.
故答案为:4π﹣8.
25.解:如图,作直径MN,使MN⊥EF于O,交AB于G,交CD于H;连接OA、OB、OC、OD;
在Rt△OBG中,BG=3cm,OB=5cm,因此OG=4cm;
同理:在Rt△OCH中,CH=4cm,OC=5cm,因此OH=3cm;
即∠DOF=∠AOM=∠COE=∠BOM,∠CON=∠DON=∠AOE=∠BOF,
因此S扇形OAE=S扇形OBF=S扇形CON=S扇形ODN
∴S阴影=S△ABE+S弓形AMB+S△CDF+S弓形CND
=S△OAB+S弓形AMB+S△OCD+S弓形CND
=S扇形OAB+S扇形OCN+S扇形ODN
=S扇形OAB+S扇形OAE+S扇形OBF
=S⊙O
=12.5πcm2.
故图中阴影部分面积之和为12.5πcm2.
26.解:连接OC、OD、CD.
∵△COD和△CDA等底等高,
∴S△COD=S△ACD.
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
∴阴影部分的面积=S扇形COD==π.
27.证明:(1)连接DO.
∵△ABC是等边三角形,
∴∠A=∠C=60°.
∵OA=OD,
∴△OAD是等边三角形.
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°﹣∠C=30°,
∴∠FDO=180°﹣∠ADO﹣∠CDF=90°,
∴DF为⊙O的切线;
(2)∵△OAD是等边三角形,
∴AD=AO=AB=2.
∴CD=AC﹣AD=2.
Rt△CDF中,
∵∠CDF=30°,
∴CF=CD=1.
∴DF=;
(3)连接OE,由(2)同理可知CE=2.
∴CF=1,
∴EF=1.
∴S直角梯形FDOE=(EF+OD) DF=,
∴S扇形OED==,
∴S阴影=S直角梯形FDOE﹣S扇形OED=﹣.
28.解:连接OD,
∵正方形的边长为1,即OC=CD=1,
∴OD=,
∴AC=OA﹣OC=﹣1,
∵DE=DC,BE=AC,弧BD=弧AD
∴S阴=长方形ACDF的面积=AC CD=﹣1.
同课章节目录
