第三章 一元一次不等式 期中复习训练卷 2021-2022学年浙教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 第三章 一元一次不等式 期中复习训练卷 2021-2022学年浙教版数学八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版八年级上册期中复习训练卷
第三章:一元一次不等式
一、单选题(每题3分,共24分)
1、(2020八上·嵊州期中)式子:① ;② ;③ ;④ ;⑤ ;⑥ 其中是不等式的有( )
A. 2个 B. 3个 C .4个 D. 5个
2、(2020八上·北仑期中)若 ,则下列各式正确的是( )
A. B. C. D.
3、(2020八上·镇海期中)下列问题的解答正确的是( )
A .m的3倍不大于n的 , 可表示为3m<
B. 是正数,可表示为
C. a是非负数,可表示为a>0
D. 的与的和是正数,可表示为>0
4、(2020八上·嘉兴期中)一元一次不等式x+2>3的解集在数轴上表示为( )
A . B.
C. D.
5、(2020八上·慈溪期中)若关于x的方程 的解是正数,则a的取值范围是( )
A. B. C. a为任何实数 D. a为大于0的数
6、(2020八上·衢州期中)已知关于x的不等式组 的整数解共有4个,则a的取值范围是( )
A. 2≤a≤3 B. 27、(2020八上·萧山期中)现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( )
A. 4辆 B. 5辆 C .6辆 D. 7辆
8、(2020八上·镇海期中)已知关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是( )
A. 或 B. 或 C. D.
二、填空题(每题3分,共24分)
9、(2020八上·北仑期中)“ 的2倍与 的差小于 ”用不等式表示________
10、(2020八上·嘉兴期中)若关于x的一元一次方程4x+m+1=x-1的解是负数,则m的取值范围是________
11、(2020八上·鄞州期中)不等式 的最大整数解是________
12、(2020八上·北仑期中)已知不等式mx+n>0的解集为x<2,则 的值是________
13、(2020八上·衢州期中)关于x的不等式组 的解集为 ;则代数式 2019b-4(a+15)3-37的值为________
14、(2020八上·柯桥期中)现定义一种新的运算:a*b=a2-2b例如3*4=32-2×4=1,则不等式(-4)*x≥0的解集为________
15、(2020八上·萧山期中)若不等式组 的解x,y满足x-y<1,则k的取值范围是________
16、(2020八上·温岭期中)如图,△ABC是等边三角形,点P是AB的中点,点M在CB的延长线上,点N在AC上,且满足∠MPN=120 已知△ABC的周长为12,设m=2AC-CM-CN,若关于 的方程 的解是正数,则 的取值范围是________
三、解答题(本题共有7题,第17-19题每题6分,第20-22题每题8分,第23题10分)
17、(2020八上·萧山期中)
(1)若x>y,比较﹣3x+5与﹣3y+5的大小,并说明理由;
(2)若x<y,且(a﹣3)x>(a﹣3)y,求a的取值范围
18、(2020八上·柯桥期中)
(1)解不等式 ,并把解表达在数轴上
(2)解不等式组
19、(2020八上·金华期中)先阅读材料,再解答问题.
解不等式:
解:把不等式 进行整理,得 ,即 ,
则有(1) ,或(2) ,
解不等式组(1),得 ,不等式组(2)无解,
所以原不等式的解集为
请根据以上方法解不等式:
20、(2020八上·金华期中)某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元。
(1)求每辆A型车和B型车的售价各为多少元;
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
21、(2020八上·温州期中)某报刊销售处从报社购进甲、乙两种报纸进行销售已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元。
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、15元销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问:该销售处每天最多购进甲种报纸多少份
22、(2020八上·柯桥期中)某家庭投资35万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电600度。
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电150度,若按每月发电600度计算,问至少需要几年才能收回成本?(不计其他费用,结果取整数)
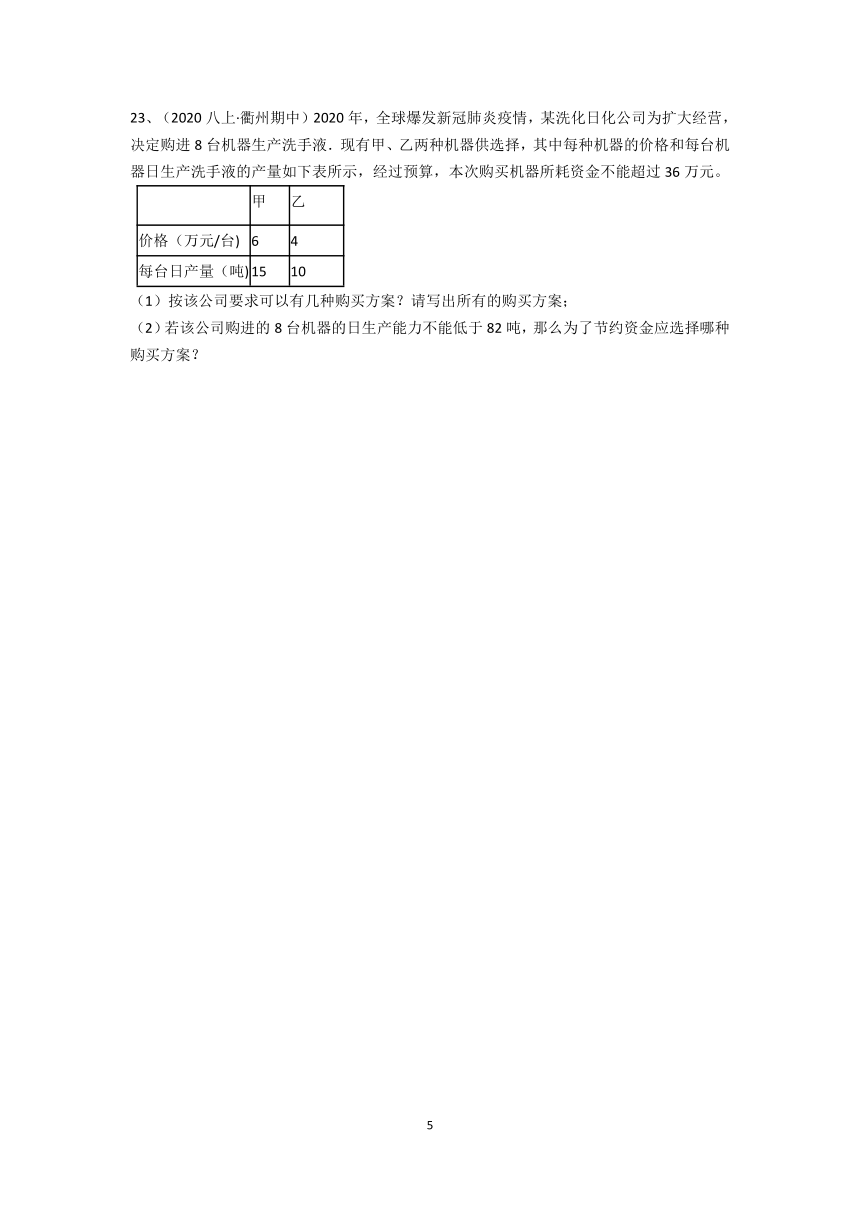
23、(2020八上·衢州期中)2020年,全球爆发新冠肺炎疫情,某洗化日化公司为扩大经营,决定购进8台机器生产洗手液.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产洗手液的产量如下表所示,经过预算,本次购买机器所耗资金不能超过36万元。
甲 乙
价格(万元/台) 6 4
每台日产量(吨) 15 10
(1)按该公司要求可以有几种购买方案?请写出所有的购买方案;
(2)若该公司购进的8台机器的日生产能力不能低于82吨,那么为了节约资金应选择哪种购买方案?
参考答案
一、单选题
1【答案】 C
【解析】【解答】解:①3<5;②4x+5>0;⑤x≠-4;⑥x+2≥x+1是不等式, ∴共4个不等式
故答案为:C
2【答案】 B
【解析】【解答】A , ,故A错误;
B ,故B正确;
C若 ,故C错误;
D ,故D错误,
故答案为:B
3【答案】 D
【解析】【解答】解:A、m的3倍不大于n的, 可表示为:3m≤n,故A不符合题意;
B、a是正数,可表示为:a>0,故B不符合题意;
C、a是非负数,可表示为a≥0,故C不符合题意;
D、x的与的和是正数,可表示为:, 故D符合题意;
故答案为:D
4【答案】 C
【解析】【解答】解:∵x+2>3, ∴x>1,
故答案为:C
5【答案】 A
【解析】【解答】解:∵3x+3a=2,∴x=,又∵方程的解为正数,∴>0, ∴a<
故答案为:A
6【答案】 B
【解析】【解答】解:由, 得:,∴不等式组的解集为<x<a,
∵不等式组的整数解有4个, ∴2<a≤3
故答案为:B
7【答案】 C
【解析】【解答】设甲种运输车至少安排x辆,5x+4(10-x)≥46,x≥6,故至少甲要6辆车.
故答案为:C.
8【答案】 B
【解析】【解答】解:解不等式组得 a-1<x<3+a
∵此不等式的任意一个x的值均不在-1≤x≤3的范围内, ∴a-1≥3,3+a≤-1, 解之:a≥4,a≤-4
故答案为:B
二、填空题
9【答案】
【解析】【解答】由题可得, ,故答案为:
10【答案】 m>-2
【解析】【解答】解:∵ 4x+m+1=x-1, 移项得:4x-x=-1-1-m, 合并同类项得:3x=-2-m,
系数化为1得:x=-, ∵该一元一次方程的解为负数, ∴-<0, 解得:m>-2,
∴m的取值范围为:m>-2
故答案为:m>-2
11【答案】 2
【解析】【解答】解: , ∴2x≤5, ∴x≤, ∴最大整数解为2
故答案为:2
12【答案】 ﹣
【解析】【解答】解:不等式mx+n>0, 移项得:mx>﹣n,
由解集为x<2,得到x<﹣ ,即 =﹣2,
∴ ,则原式=﹣,故答案为:﹣
13【答案】 2020
【解析】【解答】解:由, 得, ∴不等式组的解集为,
∵不等式组的解集为-2<x<1, ∴=-2,=1, ∴a=-5,b=3,
∴ 2019b-4(a+15)3-37 =2019×3-4×(-5+15)3-37=2020
故答案为:2020
14【答案】
【解析】【解答】解: (-4)*x≥0, ∴(-4)2-2x≥0, 解之:x≤8
故答案为:x≤8
15【答案】 k>0
【解析】【解答】解:∵ , 解得:,
∵x-y<1, ∴<1, ∴15-2k-8k<1, ∴-10k<0, ∴k>0
故答案为:k>0
16【答案】 n>10
【解析】【解答】解:如图,过点P作PE∥BC交AC于E,
∴∠APE=∠ABC=60°,∠AEP=∠ACB=60°,∴△APE是等边三角形,∴AP=AE=PE,
∵点P是AB的中点,∴AP=PB,∴PE=BP,
∵∠ABC=∠APE=∠AEP=60°,∴∠MBP=∠BPE=∠PEN=120°,∴∠MPN=∠BPE,
∴∠MPB=∠EPN,且BP=PE,∠MBP=∠PEN,∴△BPM≌△EPN(ASA)∴BM=EN,
∵△ABC的周长为12,∴AB=AC=BC=4,AP=AE=BP=2,∴CE=2,
∵m=2AC﹣CM﹣CN,∴m=8﹣BC﹣BM﹣CN=8﹣4﹣EN﹣CN=4﹣CE=2,
∵关于 的方程 的解是正数,∴x=n-10>0,∴n>10
故答案为:n>10
三、解答题
17【答案】 (1)解:-3x+5<-3y+5;理由是:
∵x>y,∴不等式两边同时乘以-3得: -3x<-3y,∴不等式两边同时加上5得:-3x+5<-3y+5
(2)解:∵x<y,且(a-3)x>(a-3)y, ∴a-3<0,解得a<3,即a的取值范围是a<3
18【答案】 (1)解:解不等式 ,并把解表达在数轴上,解:X>-2
解:解不等式组 解: 解得
由①得:2x+5≤3x+6, 解之:x≥-1; 由②得:4x-(3x+1)<2, 解之:x<3
∴不等式组的解集为:-1≤x<3
19【答案】 解:把不等式 进行整理,得 ,即 ,
则有(1) ,或(2) ,
解不等式组(1),得
不等式组(2)无解,所以原不等式的解集为
20【答案】 (1)解:每辆A型车和B型车的售价分别是x万元、y万元.则
,解得 .
答:每辆A型车的售价为18万元,每辆B型车的售价为26万元
(2)解:设购买A型车a辆,则购买B型车(6﹣a)辆,则依题意得
,解得 2≤a≤3 .
∵a是正整数,∴a=2或a=3.∴共有两种方案:
方案一:购买2辆A型车和4辆B型车;
方案二:购买3辆A型车和3辆B型车
21【答案】 (1)解:设购进甲、乙两种报纸的单价分别是x元、y元
根据题意得 解得
∴购进甲、乙两种报纸的单价分别是06元,08元
(2)解:设该销售处每天购进甲种报纸a份
根据题意得(1-06)a+(15-08)(600一a)≥300,解得a≤400∴该销售处每天最多购进甲种报纸400份
22【答案】 (1)解:设这个月晴天的天数为x,
由题意得:30x+5(30-x)=600,解得x=18,∴这个月晴天的天数为18
(2)解:设需要y年才能收回成本,由题意得 (600-150)×(052+045)×12y≥35000,5238y≥35 000,y≥67,
∵y取整数,∴至少需要7年才能收回成本
23【答案】 (1)解:设购买甲种机器x台,则购买乙种机器(8-x)台.
依题意,得6x+4×(8-x)≤36,解得 x≤2,即x可取0,1,2三个值,
∴按该公司要求可以有以下三种购买方案:
方案一:不购买甲种机器,购买乙种机器8台;
方案二:购买甲种机器1台,购买乙种机器7台;
方案三:购买甲种机器2台,购买乙种机器6台
(2)解:根据题意,15x+10(8-x)≥82, 解得:x≥,
∵x≤2,∴ ≤x≤2,∴x 可取 1,2 两个值,即有以下两种购买方案:
方案一:购买甲种机器1台,购买乙种机器7台,所耗资金为 1×6+7×4=34(万元);
方案二:购买甲种机器2台,购买乙种机器6台,所耗资金为 2×6+6×4=36(万元),
∴为了节约资金应选择方案一
第三章:一元一次不等式
一、单选题(每题3分,共24分)
1、(2020八上·嵊州期中)式子:① ;② ;③ ;④ ;⑤ ;⑥ 其中是不等式的有( )
A. 2个 B. 3个 C .4个 D. 5个
2、(2020八上·北仑期中)若 ,则下列各式正确的是( )
A. B. C. D.
3、(2020八上·镇海期中)下列问题的解答正确的是( )
A .m的3倍不大于n的 , 可表示为3m<
B. 是正数,可表示为
C. a是非负数,可表示为a>0
D. 的与的和是正数,可表示为>0
4、(2020八上·嘉兴期中)一元一次不等式x+2>3的解集在数轴上表示为( )
A . B.
C. D.
5、(2020八上·慈溪期中)若关于x的方程 的解是正数,则a的取值范围是( )
A. B. C. a为任何实数 D. a为大于0的数
6、(2020八上·衢州期中)已知关于x的不等式组 的整数解共有4个,则a的取值范围是( )
A. 2≤a≤3 B. 2
A. 4辆 B. 5辆 C .6辆 D. 7辆
8、(2020八上·镇海期中)已知关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是( )
A. 或 B. 或 C. D.
二、填空题(每题3分,共24分)
9、(2020八上·北仑期中)“ 的2倍与 的差小于 ”用不等式表示________
10、(2020八上·嘉兴期中)若关于x的一元一次方程4x+m+1=x-1的解是负数,则m的取值范围是________
11、(2020八上·鄞州期中)不等式 的最大整数解是________
12、(2020八上·北仑期中)已知不等式mx+n>0的解集为x<2,则 的值是________
13、(2020八上·衢州期中)关于x的不等式组 的解集为 ;则代数式 2019b-4(a+15)3-37的值为________
14、(2020八上·柯桥期中)现定义一种新的运算:a*b=a2-2b例如3*4=32-2×4=1,则不等式(-4)*x≥0的解集为________
15、(2020八上·萧山期中)若不等式组 的解x,y满足x-y<1,则k的取值范围是________
16、(2020八上·温岭期中)如图,△ABC是等边三角形,点P是AB的中点,点M在CB的延长线上,点N在AC上,且满足∠MPN=120 已知△ABC的周长为12,设m=2AC-CM-CN,若关于 的方程 的解是正数,则 的取值范围是________
三、解答题(本题共有7题,第17-19题每题6分,第20-22题每题8分,第23题10分)
17、(2020八上·萧山期中)
(1)若x>y,比较﹣3x+5与﹣3y+5的大小,并说明理由;
(2)若x<y,且(a﹣3)x>(a﹣3)y,求a的取值范围
18、(2020八上·柯桥期中)
(1)解不等式 ,并把解表达在数轴上
(2)解不等式组
19、(2020八上·金华期中)先阅读材料,再解答问题.
解不等式:
解:把不等式 进行整理,得 ,即 ,
则有(1) ,或(2) ,
解不等式组(1),得 ,不等式组(2)无解,
所以原不等式的解集为
请根据以上方法解不等式:
20、(2020八上·金华期中)某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元。
(1)求每辆A型车和B型车的售价各为多少元;
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
21、(2020八上·温州期中)某报刊销售处从报社购进甲、乙两种报纸进行销售已知从报社购进甲种报纸200份与乙种报纸300份共需360元,购进甲种报纸300份与乙种报纸200份共需340元。
(1)求购进甲、乙两种报纸的单价;
(2)已知销售处卖出甲、乙两种报纸的售价分别为每份1元、15元销售处每天从报社购进甲、乙两种报纸共600份,若每天能全部销售完并且销售这两种报纸的总利润不低于300元,问:该销售处每天最多购进甲种报纸多少份
22、(2020八上·柯桥期中)某家庭投资35万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电600度。
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电150度,若按每月发电600度计算,问至少需要几年才能收回成本?(不计其他费用,结果取整数)
23、(2020八上·衢州期中)2020年,全球爆发新冠肺炎疫情,某洗化日化公司为扩大经营,决定购进8台机器生产洗手液.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产洗手液的产量如下表所示,经过预算,本次购买机器所耗资金不能超过36万元。
甲 乙
价格(万元/台) 6 4
每台日产量(吨) 15 10
(1)按该公司要求可以有几种购买方案?请写出所有的购买方案;
(2)若该公司购进的8台机器的日生产能力不能低于82吨,那么为了节约资金应选择哪种购买方案?
参考答案
一、单选题
1【答案】 C
【解析】【解答】解:①3<5;②4x+5>0;⑤x≠-4;⑥x+2≥x+1是不等式, ∴共4个不等式
故答案为:C
2【答案】 B
【解析】【解答】A , ,故A错误;
B ,故B正确;
C若 ,故C错误;
D ,故D错误,
故答案为:B
3【答案】 D
【解析】【解答】解:A、m的3倍不大于n的, 可表示为:3m≤n,故A不符合题意;
B、a是正数,可表示为:a>0,故B不符合题意;
C、a是非负数,可表示为a≥0,故C不符合题意;
D、x的与的和是正数,可表示为:, 故D符合题意;
故答案为:D
4【答案】 C
【解析】【解答】解:∵x+2>3, ∴x>1,
故答案为:C
5【答案】 A
【解析】【解答】解:∵3x+3a=2,∴x=,又∵方程的解为正数,∴>0, ∴a<
故答案为:A
6【答案】 B
【解析】【解答】解:由, 得:,∴不等式组的解集为<x<a,
∵不等式组的整数解有4个, ∴2<a≤3
故答案为:B
7【答案】 C
【解析】【解答】设甲种运输车至少安排x辆,5x+4(10-x)≥46,x≥6,故至少甲要6辆车.
故答案为:C.
8【答案】 B
【解析】【解答】解:解不等式组得 a-1<x<3+a
∵此不等式的任意一个x的值均不在-1≤x≤3的范围内, ∴a-1≥3,3+a≤-1, 解之:a≥4,a≤-4
故答案为:B
二、填空题
9【答案】
【解析】【解答】由题可得, ,故答案为:
10【答案】 m>-2
【解析】【解答】解:∵ 4x+m+1=x-1, 移项得:4x-x=-1-1-m, 合并同类项得:3x=-2-m,
系数化为1得:x=-, ∵该一元一次方程的解为负数, ∴-<0, 解得:m>-2,
∴m的取值范围为:m>-2
故答案为:m>-2
11【答案】 2
【解析】【解答】解: , ∴2x≤5, ∴x≤, ∴最大整数解为2
故答案为:2
12【答案】 ﹣
【解析】【解答】解:不等式mx+n>0, 移项得:mx>﹣n,
由解集为x<2,得到x<﹣ ,即 =﹣2,
∴ ,则原式=﹣,故答案为:﹣
13【答案】 2020
【解析】【解答】解:由, 得, ∴不等式组的解集为,
∵不等式组的解集为-2<x<1, ∴=-2,=1, ∴a=-5,b=3,
∴ 2019b-4(a+15)3-37 =2019×3-4×(-5+15)3-37=2020
故答案为:2020
14【答案】
【解析】【解答】解: (-4)*x≥0, ∴(-4)2-2x≥0, 解之:x≤8
故答案为:x≤8
15【答案】 k>0
【解析】【解答】解:∵ , 解得:,
∵x-y<1, ∴<1, ∴15-2k-8k<1, ∴-10k<0, ∴k>0
故答案为:k>0
16【答案】 n>10
【解析】【解答】解:如图,过点P作PE∥BC交AC于E,
∴∠APE=∠ABC=60°,∠AEP=∠ACB=60°,∴△APE是等边三角形,∴AP=AE=PE,
∵点P是AB的中点,∴AP=PB,∴PE=BP,
∵∠ABC=∠APE=∠AEP=60°,∴∠MBP=∠BPE=∠PEN=120°,∴∠MPN=∠BPE,
∴∠MPB=∠EPN,且BP=PE,∠MBP=∠PEN,∴△BPM≌△EPN(ASA)∴BM=EN,
∵△ABC的周长为12,∴AB=AC=BC=4,AP=AE=BP=2,∴CE=2,
∵m=2AC﹣CM﹣CN,∴m=8﹣BC﹣BM﹣CN=8﹣4﹣EN﹣CN=4﹣CE=2,
∵关于 的方程 的解是正数,∴x=n-10>0,∴n>10
故答案为:n>10
三、解答题
17【答案】 (1)解:-3x+5<-3y+5;理由是:
∵x>y,∴不等式两边同时乘以-3得: -3x<-3y,∴不等式两边同时加上5得:-3x+5<-3y+5
(2)解:∵x<y,且(a-3)x>(a-3)y, ∴a-3<0,解得a<3,即a的取值范围是a<3
18【答案】 (1)解:解不等式 ,并把解表达在数轴上,解:X>-2
解:解不等式组 解: 解得
由①得:2x+5≤3x+6, 解之:x≥-1; 由②得:4x-(3x+1)<2, 解之:x<3
∴不等式组的解集为:-1≤x<3
19【答案】 解:把不等式 进行整理,得 ,即 ,
则有(1) ,或(2) ,
解不等式组(1),得
不等式组(2)无解,所以原不等式的解集为
20【答案】 (1)解:每辆A型车和B型车的售价分别是x万元、y万元.则
,解得 .
答:每辆A型车的售价为18万元,每辆B型车的售价为26万元
(2)解:设购买A型车a辆,则购买B型车(6﹣a)辆,则依题意得
,解得 2≤a≤3 .
∵a是正整数,∴a=2或a=3.∴共有两种方案:
方案一:购买2辆A型车和4辆B型车;
方案二:购买3辆A型车和3辆B型车
21【答案】 (1)解:设购进甲、乙两种报纸的单价分别是x元、y元
根据题意得 解得
∴购进甲、乙两种报纸的单价分别是06元,08元
(2)解:设该销售处每天购进甲种报纸a份
根据题意得(1-06)a+(15-08)(600一a)≥300,解得a≤400∴该销售处每天最多购进甲种报纸400份
22【答案】 (1)解:设这个月晴天的天数为x,
由题意得:30x+5(30-x)=600,解得x=18,∴这个月晴天的天数为18
(2)解:设需要y年才能收回成本,由题意得 (600-150)×(052+045)×12y≥35000,5238y≥35 000,y≥67,
∵y取整数,∴至少需要7年才能收回成本
23【答案】 (1)解:设购买甲种机器x台,则购买乙种机器(8-x)台.
依题意,得6x+4×(8-x)≤36,解得 x≤2,即x可取0,1,2三个值,
∴按该公司要求可以有以下三种购买方案:
方案一:不购买甲种机器,购买乙种机器8台;
方案二:购买甲种机器1台,购买乙种机器7台;
方案三:购买甲种机器2台,购买乙种机器6台
(2)解:根据题意,15x+10(8-x)≥82, 解得:x≥,
∵x≤2,∴ ≤x≤2,∴x 可取 1,2 两个值,即有以下两种购买方案:
方案一:购买甲种机器1台,购买乙种机器7台,所耗资金为 1×6+7×4=34(万元);
方案二:购买甲种机器2台,购买乙种机器6台,所耗资金为 2×6+6×4=36(万元),
∴为了节约资金应选择方案一
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
