3.5圆周角同步能力达标测评-2021-2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 3.5圆周角同步能力达标测评-2021-2022学年浙教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览


文档简介
2021-2022学年浙教版九年级数学上册《3.5圆周角》同步能力达标测评(附答案)
一.选择题(共11小题,满分44分)
1.如图,点A、B、P是⊙O上的三点,若∠APB=22°36 ,则∠AOB的度数为( )
A.44°72 B.45°12 C.11°18 D.22°36
2.如图,AB为⊙O的直径,点C、D在⊙O上,且AC=BC=2,∠BCD=30°,则BD的长为( )
A. B. C. D.
3.如图,AB为⊙O的直径,BC为⊙O的一条弦,半径OD⊥BC于点E,连接AD,CD,若BC=6,DE=1,则的值为( )
A. B. C. D.
4.如图,在⊙O中,,∠AOB=40°,则∠CAD的度数为( )
A.10° B.20° C.30° D.40°
5.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,若∠AEC=64°,连接AD,则∠BAD的度数为( )
A.19° B.21° C.23° D.26°
6.如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,连接AC.若∠DAB=40°,则∠D的度数为( )
A.70° B.120° C.140° D.110°
7.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A.115° B.130° C.65° D.50°
8.如图,在⊙O中,点D为的中点,CD为⊙O的直径,AE∥BC交⊙O于点E.连接CE.若∠ECD=50°,则∠DCB=( )
A.10° B.15° C.20° D.25°
9.如图,在⊙O中,点A、B、C均在圆上,连接OA、OB、OC、BC、AC,若AC∥OB,OC=4,AB=5,则BC=( )
A.5 B. C. D.8
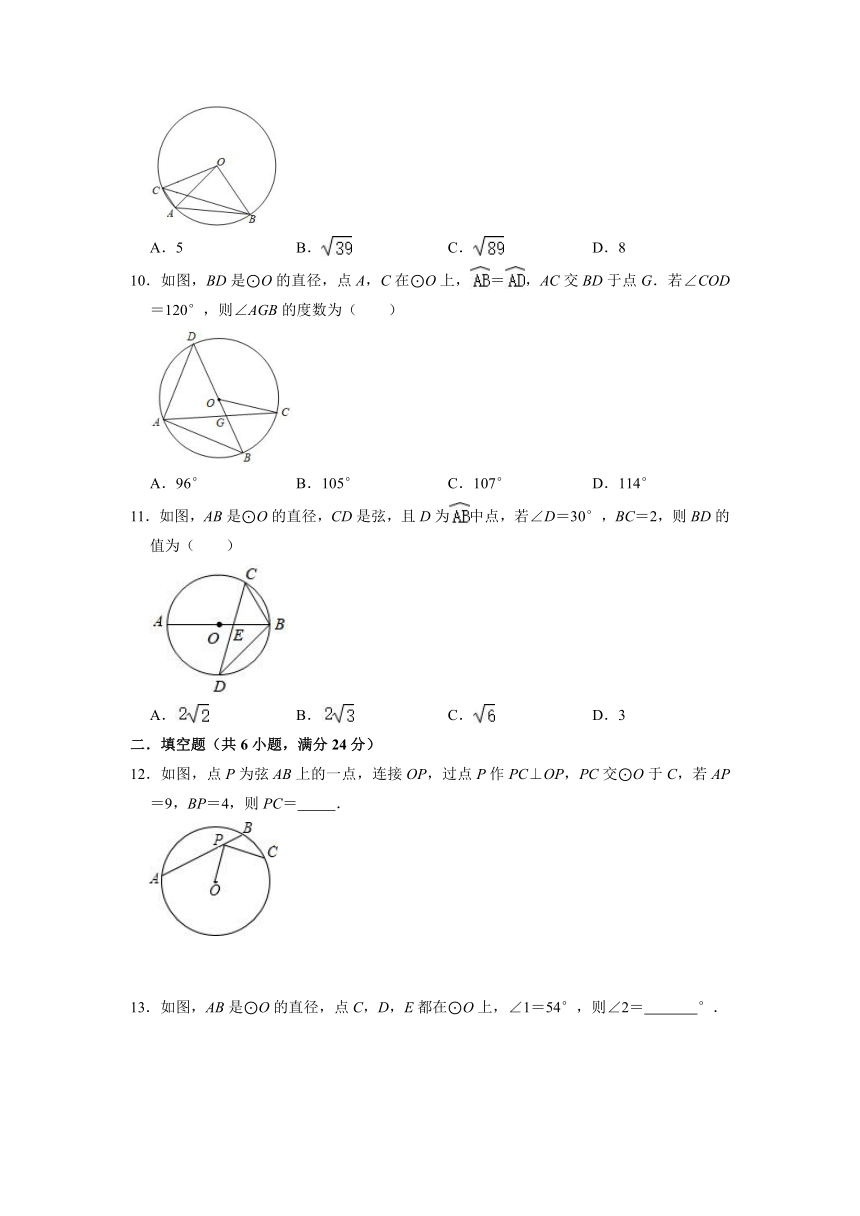
10.如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=120°,则∠AGB的度数为( )
A.96° B.105° C.107° D.114°
11.如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
二.填空题(共6小题,满分24分)
12.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C,若AP=9,BP=4,则PC= .
13.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=54°,则∠2= °.
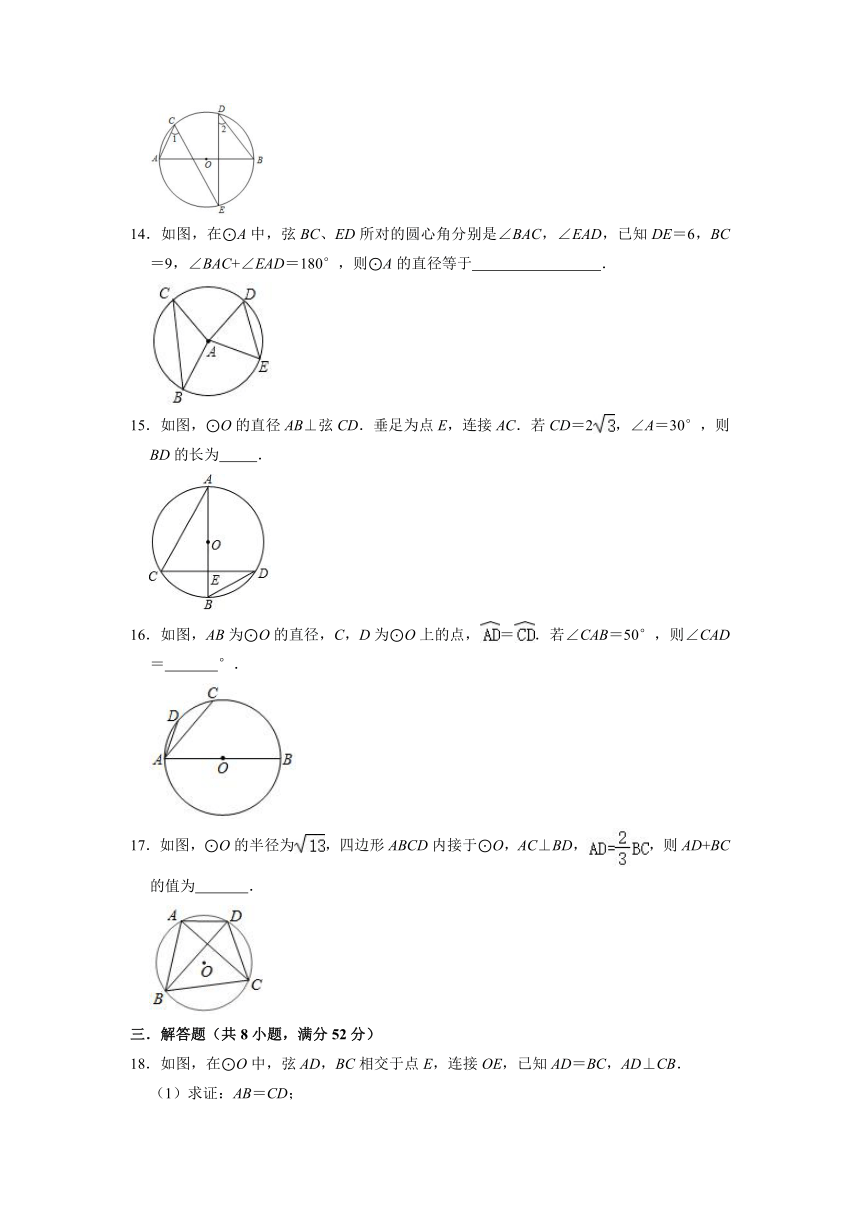
14.如图,在⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,BC=9,∠BAC+∠EAD=180°,则⊙A的直径等于 .
15.如图,⊙O的直径AB⊥弦CD.垂足为点E,连接AC.若CD=2,∠A=30°,则BD的长为 .
16.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= °.
17.如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为 .
三.解答题(共8小题,满分52分)
18.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
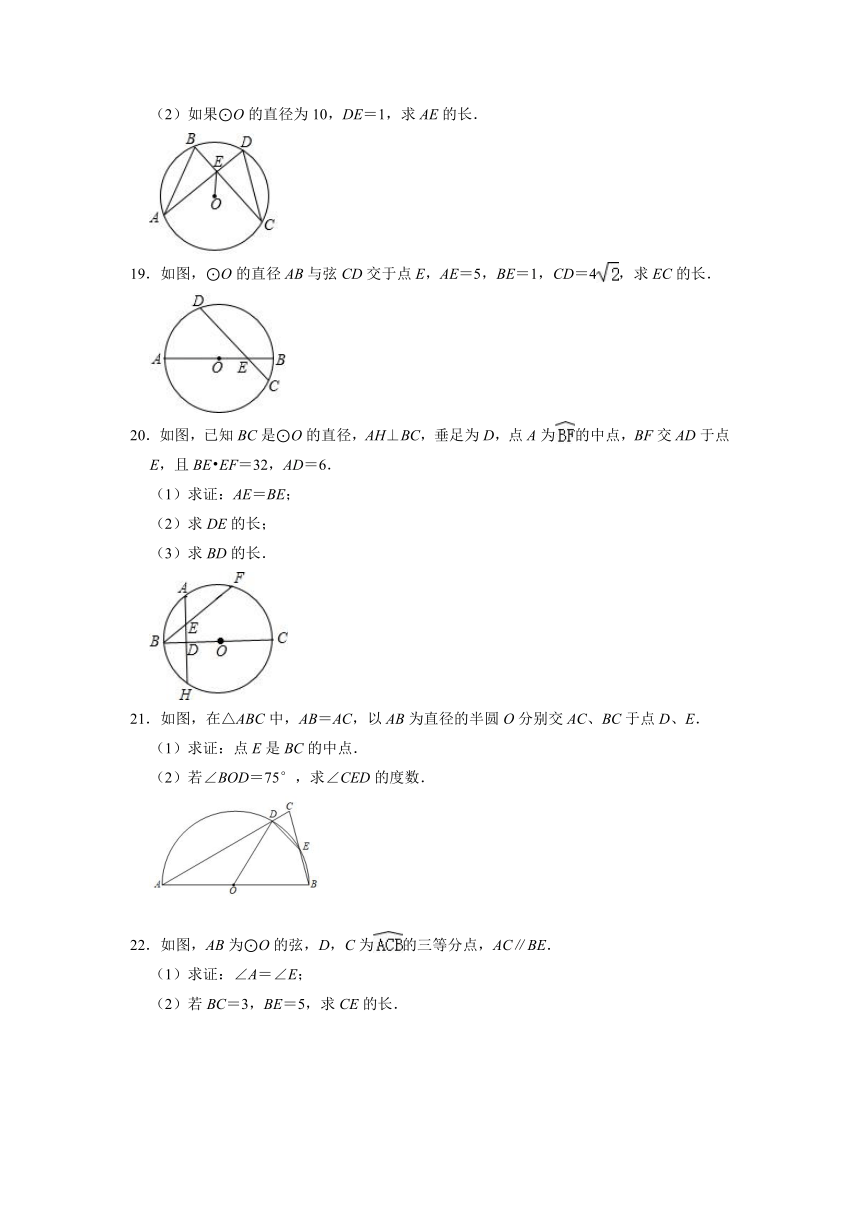
(2)如果⊙O的直径为10,DE=1,求AE的长.
19.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,求EC的长.
20.如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为的中点,BF交AD于点E,且BE EF=32,AD=6.
(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长.
21.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
22.如图,AB为⊙O的弦,D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
23.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长.
24.如图,AB是半圆O的直径,D是的中点,DE⊥AB于点E,AC交DE于点F.
(1)求证:∠DAF=∠ADF;
(2)若CD=2,半圆O的半径为5,求BC的长.
25.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案
一.选择题(共11小题,满分44分)
1.解:由圆周角定理知,∠APB=∠AOB,
∵∠APB=22°36 ,
∴∠AOB=45°12 ,
故选:B.
2.解:如图,连接AD,
∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AC=BC=2,
∴AB===2,
∵∠BCD=30°,
∴∠BAD=∠BCD=30°,
在Rt△ABD中,AB=2,
∴BD=AB=.
故选:C.
3.解:∵OD⊥BC,BC=6,
∴∠BEO=90°,BE=CE=BC=3,
在Rt△BEO中,BE2+OE2=OB2,DE=1,
即32+(OD﹣1)2=OD2,
∴OD=5,
∵∠ADC=∠ABC,
∴==,
故选:A.
4.解:如图,连结OC、OD,
在⊙O中,∠AOB=40°,=,
∴∠COD=∠AOB=40°,
∴∠CAD=∠COD=20°,
故选:B.
5.解:∵OC⊥AB,
∴∠COA=90°,
∴∠D=∠COA=45°,
∵∠AEC=∠D+∠BAD,∠AEC=64°,
∴∠BAD=64°﹣45°=19°,
故选:A.
6.解:∵BC=CD,
∴=,
∵∠DAB=40°,
∴∠BAC=∠DAB=20°,
∵AB为直径,
∴∠ACB=90°,
∴∠B=90°﹣∠BAC=70°,
∵四边形ABCD内接于⊙O,
∴∠D=180°﹣∠B=110°,
故选:D.
7.解:∵∠BOD=130°,
∴∠BCD=∠BOD=65°,
故选:C.
8.解:连接AD,如图,
∵四边形ADCE为圆的内接四边形,
∴∠EAD+∠ECD=180°,
∴∠EAD=180°﹣50°=130°,即∠EAB+∠BAD=130°,
∵AE∥BC,
∴∠EAB+∠B=180°,
∴∠EAB=180°﹣∠B,
∴180°﹣∠B+∠BAD=130°,即∠B﹣∠BAD=50°,
∵点D为的中点,CD为直径,
∴∠BAD=∠BCD,CD⊥AB,
∴∠B+∠BCD=90°,即∠B=90°﹣∠BCD,
∴90°﹣∠BCD﹣∠BCD=50°,解得∠BCD=20°.
故选:C.
9.BC解:如图,过点O作OK⊥AB于K,过点A作AH⊥OB于H,过点C作CJ⊥BO交BO的延长线于J.
∵AC∥BO,CJ⊥BO,AH⊥BO,
∴CJ=AH,
∵∠CJO=∠AHO,CO=AO,
∴Rt△CJO≌Rt△AHO(HL),
∴OJ=OH,
∵OA=OB,OK⊥AB,
∴AK=BK=.
∴OK===,
∵ AB OK= OB AH,
∴AH=CJ===,
∴OJ=OH===,
∴BJ=OJ+OB=,
∴BC===,
解法二:延长CO交⊙O于点D,连接BD.
∵CD是直径,
∴∠CBD=90°,
∵AC∥OB,
∴∠ACO=∠BOD,∠CAO=∠AOB,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠BOD=∠AOB,
∴BD=AB=5,
∵OC=4,
∴CD=2OC=8,
在Rt△BCD中,BC===,
故选:B.
10.解:∵BD是⊙O的直径,∠COD=120°,
∴∠BOC=180°﹣∠COD=60°,
∴∠BAC=∠BOC=30°,
∵BD是⊙O的直径,=,
∴∠BAD=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠B=45°,
∴∠AGB=180°﹣∠B﹣∠BAG=180°﹣45°﹣30°=105°.
故选:B.
11.解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
二.填空题(共6小题,满分24分)
12.解:延长CP交⊙O于点D,
∵PC⊥OP,
∴PC=PD,
∵PC PD=PA PB,
∴PC2=PA PB,
∵AP=9,BP=4,
∴PC2=4×9,
解得:PC=6.
故答案为:6.
13.解:连接OE,如图,
∵∠AOE=2∠1=2×54°=108°,
∴∠BOE=180°﹣∠AOE=180°﹣108°=72°,
∵∠BOE=2∠2,
∴∠2=×72°=36°.
故答案为:36.
14.解:作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵CF是直径,
∴∠CBF=90°,
∴CF===3,
故答案为:3.
15.解:如图所示,则∠BDC=∠A=30°,
∵AB⊥CD,
∴CE=DE=CD=,∠BED=90°,
∴BD=2BE,
设BE=x,则BD=2x,
由勾股定理得:BD2=BE2+ED2,
,
x=1,
∴BD=2,
故答案为:2.
16.解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠CAB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
17.解:作直径BE,连接DE,EC.
∵BE是直径,
∴∠BDE=∠BCE=90°,
∴BD⊥DE,
∵AC⊥BD,
∴DE∥AC,
∴∠CDE=∠ACD,
∴=,
∴AD=EC,
∵AD=BC,
∴EC=BC,
∴可以假设EC=2k,BC=3k,
∵BC2+EC2=BE2,
∴(3k)2+(2k)2=(2)2,
∴k=2或﹣2(舍弃),
∴BC=6,EC=4,
∴AD=EC=4,
∴AD+BC=10,
故答案为10.
三.解答题(共8小题,满分52分)
18.(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=5.
则AF=3+1=4,即AE=AF+3=7.
19.解:设EC=x,则ED=CD﹣CE=4﹣x,
根据题意得AE BE=CE DE,
所以x(4﹣x)=5 1,
整理得x2﹣4x+5=0,
解得x=2±,
即EC的长为2+或2﹣.
20.(1)证明:连AF,AB,AC.因为A是的中点,
∴∠ABE=∠AFB.
又∠AFB=∠ACB,
∴∠ABE=∠ACB.
∵BC为直径,
∴∠BAC=90°,AH⊥BC.
∴∠BAE=∠ACB.
∴∠ABE=∠BAE.
∴AE=BE.
(2)解:设DE=x(x>0),由AD=6,BE EF=32,AE EH=BE EF,
则(6﹣x)(6+x)=32,
解得x=2,
即DE的长为2;
(3)解:由(1)、(2)有:BE=AE=6﹣2=4,
在Rt△BDE中,BD==.
21.(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
22.(1)证明:
∵AC∥BE,
∴∠E═∠ACD,
∵D,C为的三等分点,
∴==,
∴∠ACD═∠A,
∴∠E═∠A,
(2)解:由(1)知==,
∴∠D═∠CBD═∠A═∠E,
∴BE═BD═5,BC═CD═3,
解得DE═,
∴CE═DE﹣CD═﹣3═.
23.解:(1)如图,连接BD,
∵∠ACD=30°,
∴∠B=∠ACD=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣∠B=60°;
(2)∵∠ADB=90°,∠B=30°,AB=4,
∴AD=AB=2,
∵∠DAB=60°,DE⊥AB,且AB是直径,
∴EF=DE=,
∴DF=2DE=2.
24.(1)证明:连接BD,
∵D为的中点,
∴=,
∴∠DAC=∠ABD,
∵AB为半圆O的直径,DE⊥AB,
∴∠DEA=∠ADB=90°,
∴∠ADF+∠DAE=∠DAE+∠ABD=90°,
∴∠ADF=∠ABD,
∴∠DAF=∠ADF;
(2)解:连接OD交AC于H,
∵=,OD过O,
∴OD⊥AC,AD=CD=2,
在Rt△AOH中,AH2=OA2﹣OH2,
在Rt△ADH中,AH2=AD2﹣DH2,
∴OA2﹣OH2=AD2﹣DH2,
即52﹣OH2=(2)2﹣(5﹣OH)2,
解得:OH=3,
∵D为的中点,OD过O,
∴AH=CH,
∵AO=BO,
∴OH=BC,
∴BC=2OH=6.
25.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
一.选择题(共11小题,满分44分)
1.如图,点A、B、P是⊙O上的三点,若∠APB=22°36 ,则∠AOB的度数为( )
A.44°72 B.45°12 C.11°18 D.22°36
2.如图,AB为⊙O的直径,点C、D在⊙O上,且AC=BC=2,∠BCD=30°,则BD的长为( )
A. B. C. D.
3.如图,AB为⊙O的直径,BC为⊙O的一条弦,半径OD⊥BC于点E,连接AD,CD,若BC=6,DE=1,则的值为( )
A. B. C. D.
4.如图,在⊙O中,,∠AOB=40°,则∠CAD的度数为( )
A.10° B.20° C.30° D.40°
5.如图,AB为⊙O的直径,点C在⊙O上,且CO⊥AB于点O,弦CD与AB相交于点E,若∠AEC=64°,连接AD,则∠BAD的度数为( )
A.19° B.21° C.23° D.26°
6.如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,连接AC.若∠DAB=40°,则∠D的度数为( )
A.70° B.120° C.140° D.110°
7.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A.115° B.130° C.65° D.50°
8.如图,在⊙O中,点D为的中点,CD为⊙O的直径,AE∥BC交⊙O于点E.连接CE.若∠ECD=50°,则∠DCB=( )
A.10° B.15° C.20° D.25°
9.如图,在⊙O中,点A、B、C均在圆上,连接OA、OB、OC、BC、AC,若AC∥OB,OC=4,AB=5,则BC=( )
A.5 B. C. D.8
10.如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=120°,则∠AGB的度数为( )
A.96° B.105° C.107° D.114°
11.如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
二.填空题(共6小题,满分24分)
12.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C,若AP=9,BP=4,则PC= .
13.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=54°,则∠2= °.
14.如图,在⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,BC=9,∠BAC+∠EAD=180°,则⊙A的直径等于 .
15.如图,⊙O的直径AB⊥弦CD.垂足为点E,连接AC.若CD=2,∠A=30°,则BD的长为 .
16.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= °.
17.如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为 .
三.解答题(共8小题,满分52分)
18.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
19.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,求EC的长.
20.如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为的中点,BF交AD于点E,且BE EF=32,AD=6.
(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长.
21.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
22.如图,AB为⊙O的弦,D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
23.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长.
24.如图,AB是半圆O的直径,D是的中点,DE⊥AB于点E,AC交DE于点F.
(1)求证:∠DAF=∠ADF;
(2)若CD=2,半圆O的半径为5,求BC的长.
25.如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
参考答案
一.选择题(共11小题,满分44分)
1.解:由圆周角定理知,∠APB=∠AOB,
∵∠APB=22°36 ,
∴∠AOB=45°12 ,
故选:B.
2.解:如图,连接AD,
∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,AC=BC=2,
∴AB===2,
∵∠BCD=30°,
∴∠BAD=∠BCD=30°,
在Rt△ABD中,AB=2,
∴BD=AB=.
故选:C.
3.解:∵OD⊥BC,BC=6,
∴∠BEO=90°,BE=CE=BC=3,
在Rt△BEO中,BE2+OE2=OB2,DE=1,
即32+(OD﹣1)2=OD2,
∴OD=5,
∵∠ADC=∠ABC,
∴==,
故选:A.
4.解:如图,连结OC、OD,
在⊙O中,∠AOB=40°,=,
∴∠COD=∠AOB=40°,
∴∠CAD=∠COD=20°,
故选:B.
5.解:∵OC⊥AB,
∴∠COA=90°,
∴∠D=∠COA=45°,
∵∠AEC=∠D+∠BAD,∠AEC=64°,
∴∠BAD=64°﹣45°=19°,
故选:A.
6.解:∵BC=CD,
∴=,
∵∠DAB=40°,
∴∠BAC=∠DAB=20°,
∵AB为直径,
∴∠ACB=90°,
∴∠B=90°﹣∠BAC=70°,
∵四边形ABCD内接于⊙O,
∴∠D=180°﹣∠B=110°,
故选:D.
7.解:∵∠BOD=130°,
∴∠BCD=∠BOD=65°,
故选:C.
8.解:连接AD,如图,
∵四边形ADCE为圆的内接四边形,
∴∠EAD+∠ECD=180°,
∴∠EAD=180°﹣50°=130°,即∠EAB+∠BAD=130°,
∵AE∥BC,
∴∠EAB+∠B=180°,
∴∠EAB=180°﹣∠B,
∴180°﹣∠B+∠BAD=130°,即∠B﹣∠BAD=50°,
∵点D为的中点,CD为直径,
∴∠BAD=∠BCD,CD⊥AB,
∴∠B+∠BCD=90°,即∠B=90°﹣∠BCD,
∴90°﹣∠BCD﹣∠BCD=50°,解得∠BCD=20°.
故选:C.
9.BC解:如图,过点O作OK⊥AB于K,过点A作AH⊥OB于H,过点C作CJ⊥BO交BO的延长线于J.
∵AC∥BO,CJ⊥BO,AH⊥BO,
∴CJ=AH,
∵∠CJO=∠AHO,CO=AO,
∴Rt△CJO≌Rt△AHO(HL),
∴OJ=OH,
∵OA=OB,OK⊥AB,
∴AK=BK=.
∴OK===,
∵ AB OK= OB AH,
∴AH=CJ===,
∴OJ=OH===,
∴BJ=OJ+OB=,
∴BC===,
解法二:延长CO交⊙O于点D,连接BD.
∵CD是直径,
∴∠CBD=90°,
∵AC∥OB,
∴∠ACO=∠BOD,∠CAO=∠AOB,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠BOD=∠AOB,
∴BD=AB=5,
∵OC=4,
∴CD=2OC=8,
在Rt△BCD中,BC===,
故选:B.
10.解:∵BD是⊙O的直径,∠COD=120°,
∴∠BOC=180°﹣∠COD=60°,
∴∠BAC=∠BOC=30°,
∵BD是⊙O的直径,=,
∴∠BAD=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠B=45°,
∴∠AGB=180°﹣∠B﹣∠BAG=180°﹣45°﹣30°=105°.
故选:B.
11.解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
二.填空题(共6小题,满分24分)
12.解:延长CP交⊙O于点D,
∵PC⊥OP,
∴PC=PD,
∵PC PD=PA PB,
∴PC2=PA PB,
∵AP=9,BP=4,
∴PC2=4×9,
解得:PC=6.
故答案为:6.
13.解:连接OE,如图,
∵∠AOE=2∠1=2×54°=108°,
∴∠BOE=180°﹣∠AOE=180°﹣108°=72°,
∵∠BOE=2∠2,
∴∠2=×72°=36°.
故答案为:36.
14.解:作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵CF是直径,
∴∠CBF=90°,
∴CF===3,
故答案为:3.
15.解:如图所示,则∠BDC=∠A=30°,
∵AB⊥CD,
∴CE=DE=CD=,∠BED=90°,
∴BD=2BE,
设BE=x,则BD=2x,
由勾股定理得:BD2=BE2+ED2,
,
x=1,
∴BD=2,
故答案为:2.
16.解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠CAB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
17.解:作直径BE,连接DE,EC.
∵BE是直径,
∴∠BDE=∠BCE=90°,
∴BD⊥DE,
∵AC⊥BD,
∴DE∥AC,
∴∠CDE=∠ACD,
∴=,
∴AD=EC,
∵AD=BC,
∴EC=BC,
∴可以假设EC=2k,BC=3k,
∵BC2+EC2=BE2,
∴(3k)2+(2k)2=(2)2,
∴k=2或﹣2(舍弃),
∴BC=6,EC=4,
∴AD=EC=4,
∴AD+BC=10,
故答案为10.
三.解答题(共8小题,满分52分)
18.(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=5.
则AF=3+1=4,即AE=AF+3=7.
19.解:设EC=x,则ED=CD﹣CE=4﹣x,
根据题意得AE BE=CE DE,
所以x(4﹣x)=5 1,
整理得x2﹣4x+5=0,
解得x=2±,
即EC的长为2+或2﹣.
20.(1)证明:连AF,AB,AC.因为A是的中点,
∴∠ABE=∠AFB.
又∠AFB=∠ACB,
∴∠ABE=∠ACB.
∵BC为直径,
∴∠BAC=90°,AH⊥BC.
∴∠BAE=∠ACB.
∴∠ABE=∠BAE.
∴AE=BE.
(2)解:设DE=x(x>0),由AD=6,BE EF=32,AE EH=BE EF,
则(6﹣x)(6+x)=32,
解得x=2,
即DE的长为2;
(3)解:由(1)、(2)有:BE=AE=6﹣2=4,
在Rt△BDE中,BD==.
21.(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
22.(1)证明:
∵AC∥BE,
∴∠E═∠ACD,
∵D,C为的三等分点,
∴==,
∴∠ACD═∠A,
∴∠E═∠A,
(2)解:由(1)知==,
∴∠D═∠CBD═∠A═∠E,
∴BE═BD═5,BC═CD═3,
解得DE═,
∴CE═DE﹣CD═﹣3═.
23.解:(1)如图,连接BD,
∵∠ACD=30°,
∴∠B=∠ACD=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣∠B=60°;
(2)∵∠ADB=90°,∠B=30°,AB=4,
∴AD=AB=2,
∵∠DAB=60°,DE⊥AB,且AB是直径,
∴EF=DE=,
∴DF=2DE=2.
24.(1)证明:连接BD,
∵D为的中点,
∴=,
∴∠DAC=∠ABD,
∵AB为半圆O的直径,DE⊥AB,
∴∠DEA=∠ADB=90°,
∴∠ADF+∠DAE=∠DAE+∠ABD=90°,
∴∠ADF=∠ABD,
∴∠DAF=∠ADF;
(2)解:连接OD交AC于H,
∵=,OD过O,
∴OD⊥AC,AD=CD=2,
在Rt△AOH中,AH2=OA2﹣OH2,
在Rt△ADH中,AH2=AD2﹣DH2,
∴OA2﹣OH2=AD2﹣DH2,
即52﹣OH2=(2)2﹣(5﹣OH)2,
解得:OH=3,
∵D为的中点,OD过O,
∴AH=CH,
∵AO=BO,
∴OH=BC,
∴BC=2OH=6.
25.证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
同课章节目录
