2021-2022学年 浙教版九年级数学上册第四章 相似三角形 单元检测试卷(word版、含答案)
文档属性
| 名称 | 2021-2022学年 浙教版九年级数学上册第四章 相似三角形 单元检测试卷(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 15:35:23 | ||
图片预览

文档简介
2021-2022学年度第一学期浙教版九年级数学上册
第四章 相似三角形 单元检测试卷
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
1.已知的三边长分别为,,,与它相似的的最小边长为,则的周长为( )
A. B. C. D.
2.在比例尺为的地图上,量得、两地的距离为厘米,则、两地的实际距离是( )
A.千米 B.千米 C.千米 D.千米
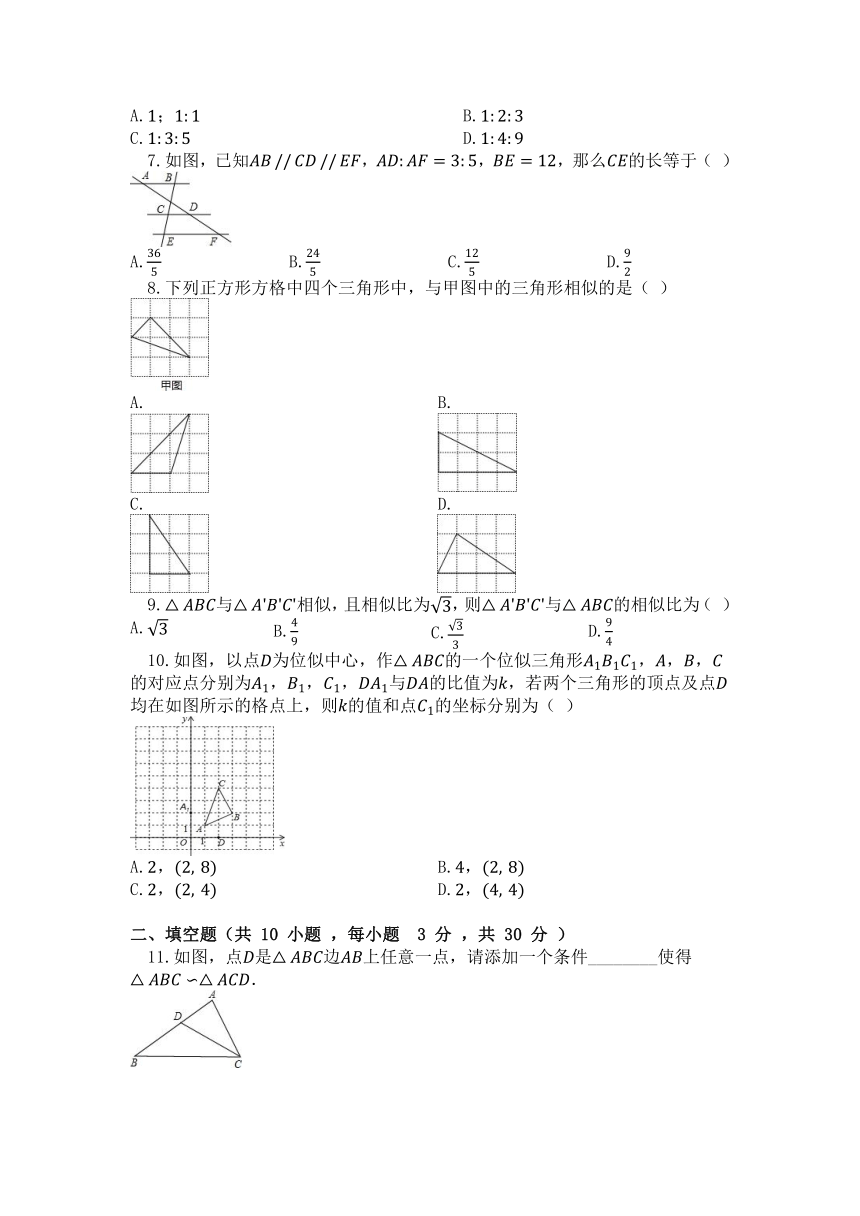
3.如图,,点,分别在,上,,,则长为( )
A. B. C. D.
4.如图,要使,则下列选项中不能作为条件添加的是( )
A. B.
C. D.
5.如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫做黄金三角形.已知,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为( )
A. B.
C. D.
6.如图,在中,,且,被、分成三部分,且三部分面积分别为,,,则
A.; B.
C. D.
7.如图,已知,,,那么的长等于( )
A. B. C. D.
8.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
9.与相似,且相似比为,则与的相似比为( )
A. B. C. D.
10.如图,以点为位似中心,作的一个位似三角形,,,的对应点分别为,,,与的比值为,若两个三角形的顶点及点均在如图所示的格点上,则的值和点的坐标分别为( )
A., B.,
C., D.,
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
11.如图,点是边上任意一点,请添加一个条件________使得.
12.如图,在中,为上一点,则下列四个条件中
;;;,
其中能满足和相似的条件有________.
13.如图,中,,,是的中点,是上一点,,若,则________.
14.如图,身高为米的学生想测量学校旗杆的高度,当他站在处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得米,米,则旗杆的高度是________米.
15.如图,中,若,,,则的长为________ .
16.如图,在矩形中,截去一个正方形后,使剩下的矩形对开后与原矩形相似,那么原矩形中________.
17.某数学兴趣小组测得小强的影长是,同一时刻旗杆的影长是.已知小强的身高为,则旗杆的高度为________.
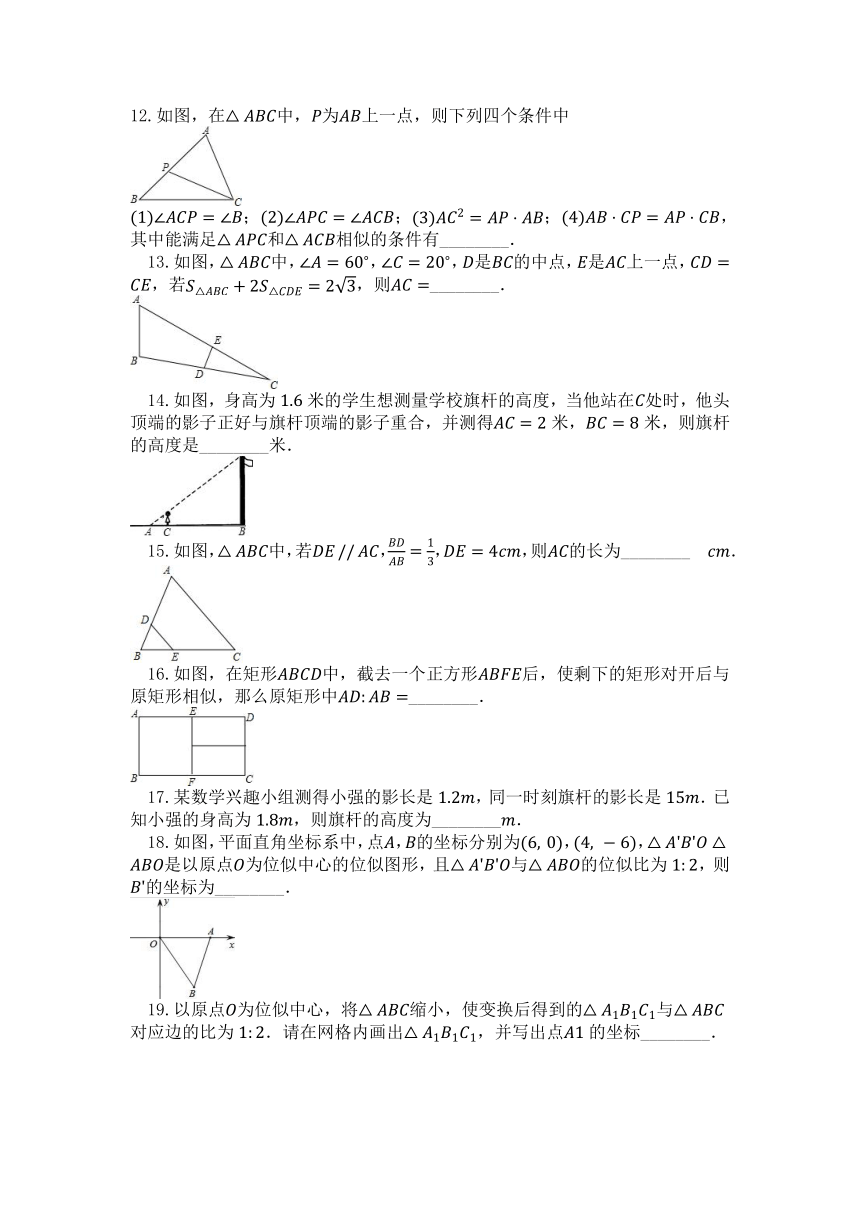
18.如图,平面直角坐标系中,点,的坐标分别为,,是以原点为位似中心的位似图形,且与的位似比为,则的坐标为________.
19.以原点为位似中心,将缩小,使变换后得到的与对应边的比为.请在网格内画出,并写出点的坐标________.
20.如图,已知.,,则________.
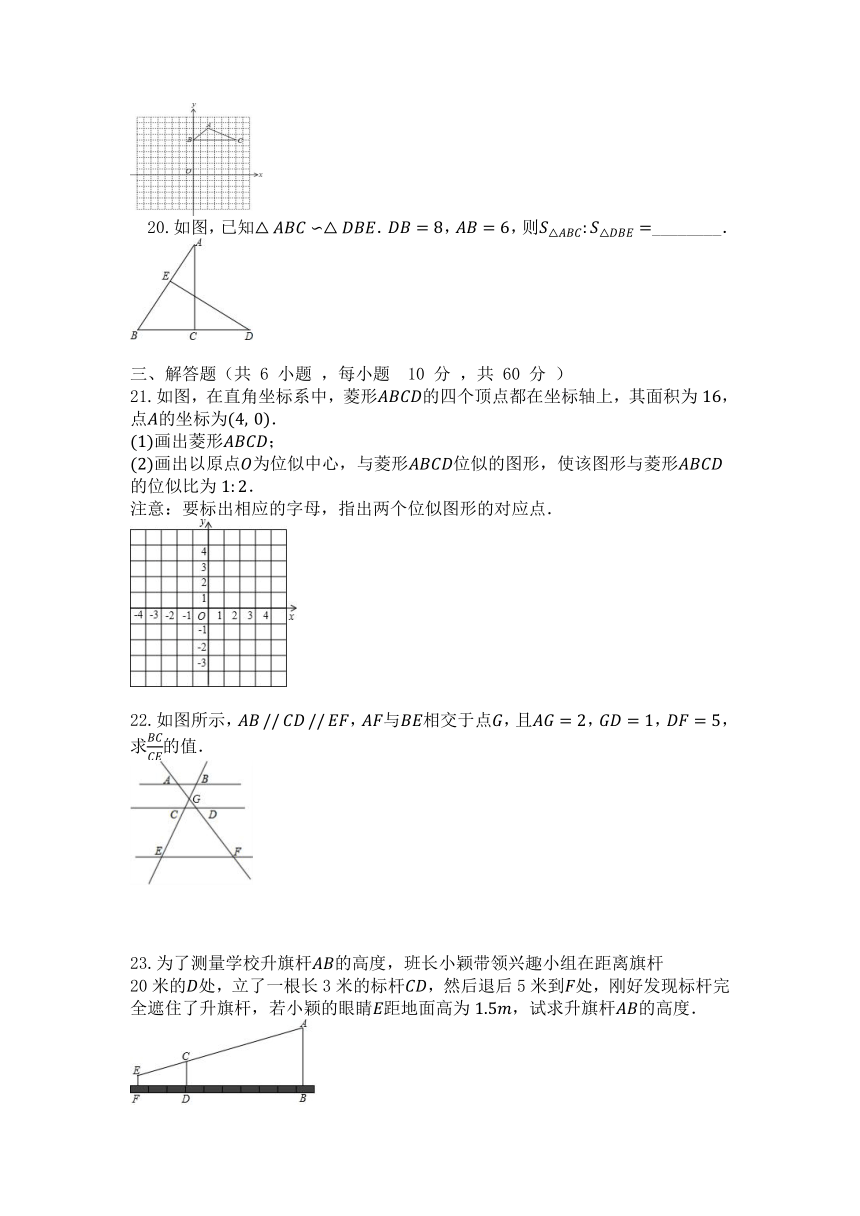
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
21.如图,在直角坐标系中,菱形的四个顶点都在坐标轴上,其面积为,点的坐标为.
画出菱形;
画出以原点为位似中心,与菱形位似的图形,使该图形与菱形的位似比为.
注意:要标出相应的字母,指出两个位似图形的对应点.
22.如图所示,,与相交于点,且,,,求的值.
23.为了测量学校升旗杆的高度,班长小颖带领兴趣小组在距离旗杆
20米的处,立了一根长3米的标杆,然后退后5米到处,刚好发现标杆完全遮住了升旗杆,若小颖的眼睛距地面高为,试求升旗杆的高度.
24.有一块三角形的余料,要把它加工成矩形的零件,已知,,高,矩形的边在边上,、分别在、上.
若,求的长;
问长为多少时,矩形的面积是三角形的面积的.
25. 如图,中,,,,说明:
;
;
若取边的中点,则为等边三角形.
26.如图是一位同学用手电来测量某古城墙高度的示意图,点处放一水平的平面镜,光线从点出发经平面镜反射后刚好射到古城墙的顶端处,已知,,且测得米,米,米.你能求出该古城墙的高度吗?(平面镜的厚度忽略不计)
答案
一.选择题
1.C
2.C
3.A
4.C
5.C
6.C
7.B
8.B
9.C
10.A
二.填空题
11.
12.,.
13.
14.
15.
16.或
17.
18.或
19.
20.
三.解答题
21.解:如图没有标出字母或没有指出对应的字母给一半分
22.解:如图,∵,
∴,而,,
∴的值为.
23.解:过点作,交于点,交于点,
则,,,,
∵,
∴,
∴,
∴ ,
∴,即旗杆的高为.
24.解:∵,高,的长为、的长为,四边形是矩形,
∴,,,
∴,
∴,即.
∵,
∴,即;∵由可知,,
∴.
∵矩形的面积是三角形的面积的,
∴,即,解得,,
∴当长为或时,矩形的面积是三角形的面积的.
25.证明:∵,,
∴,
又∵,
∴;由得:,
∴,
又∵,
∴;∵,,
∴,
∴,
由得:,
∴,
∴,
又∵是的中点,
∴,,
∴,
∴为等边三角形.
26.该古城墙的高度是米.
第四章 相似三角形 单元检测试卷
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
1.已知的三边长分别为,,,与它相似的的最小边长为,则的周长为( )
A. B. C. D.
2.在比例尺为的地图上,量得、两地的距离为厘米,则、两地的实际距离是( )
A.千米 B.千米 C.千米 D.千米
3.如图,,点,分别在,上,,,则长为( )
A. B. C. D.
4.如图,要使,则下列选项中不能作为条件添加的是( )
A. B.
C. D.
5.如图所示,顶角为的等腰三角形,其底边与腰之比等于,这样的三角形叫做黄金三角形.已知,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第个黄金三角形的周长为( )
A. B.
C. D.
6.如图,在中,,且,被、分成三部分,且三部分面积分别为,,,则
A.; B.
C. D.
7.如图,已知,,,那么的长等于( )
A. B. C. D.
8.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
9.与相似,且相似比为,则与的相似比为( )
A. B. C. D.
10.如图,以点为位似中心,作的一个位似三角形,,,的对应点分别为,,,与的比值为,若两个三角形的顶点及点均在如图所示的格点上,则的值和点的坐标分别为( )
A., B.,
C., D.,
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
11.如图,点是边上任意一点,请添加一个条件________使得.
12.如图,在中,为上一点,则下列四个条件中
;;;,
其中能满足和相似的条件有________.
13.如图,中,,,是的中点,是上一点,,若,则________.
14.如图,身高为米的学生想测量学校旗杆的高度,当他站在处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得米,米,则旗杆的高度是________米.
15.如图,中,若,,,则的长为________ .
16.如图,在矩形中,截去一个正方形后,使剩下的矩形对开后与原矩形相似,那么原矩形中________.
17.某数学兴趣小组测得小强的影长是,同一时刻旗杆的影长是.已知小强的身高为,则旗杆的高度为________.
18.如图,平面直角坐标系中,点,的坐标分别为,,是以原点为位似中心的位似图形,且与的位似比为,则的坐标为________.
19.以原点为位似中心,将缩小,使变换后得到的与对应边的比为.请在网格内画出,并写出点的坐标________.
20.如图,已知.,,则________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
21.如图,在直角坐标系中,菱形的四个顶点都在坐标轴上,其面积为,点的坐标为.
画出菱形;
画出以原点为位似中心,与菱形位似的图形,使该图形与菱形的位似比为.
注意:要标出相应的字母,指出两个位似图形的对应点.
22.如图所示,,与相交于点,且,,,求的值.
23.为了测量学校升旗杆的高度,班长小颖带领兴趣小组在距离旗杆
20米的处,立了一根长3米的标杆,然后退后5米到处,刚好发现标杆完全遮住了升旗杆,若小颖的眼睛距地面高为,试求升旗杆的高度.
24.有一块三角形的余料,要把它加工成矩形的零件,已知,,高,矩形的边在边上,、分别在、上.
若,求的长;
问长为多少时,矩形的面积是三角形的面积的.
25. 如图,中,,,,说明:
;
;
若取边的中点,则为等边三角形.
26.如图是一位同学用手电来测量某古城墙高度的示意图,点处放一水平的平面镜,光线从点出发经平面镜反射后刚好射到古城墙的顶端处,已知,,且测得米,米,米.你能求出该古城墙的高度吗?(平面镜的厚度忽略不计)
答案
一.选择题
1.C
2.C
3.A
4.C
5.C
6.C
7.B
8.B
9.C
10.A
二.填空题
11.
12.,.
13.
14.
15.
16.或
17.
18.或
19.
20.
三.解答题
21.解:如图没有标出字母或没有指出对应的字母给一半分
22.解:如图,∵,
∴,而,,
∴的值为.
23.解:过点作,交于点,交于点,
则,,,,
∵,
∴,
∴,
∴ ,
∴,即旗杆的高为.
24.解:∵,高,的长为、的长为,四边形是矩形,
∴,,,
∴,
∴,即.
∵,
∴,即;∵由可知,,
∴.
∵矩形的面积是三角形的面积的,
∴,即,解得,,
∴当长为或时,矩形的面积是三角形的面积的.
25.证明:∵,,
∴,
又∵,
∴;由得:,
∴,
又∵,
∴;∵,,
∴,
∴,
由得:,
∴,
∴,
又∵是的中点,
∴,,
∴,
∴为等边三角形.
26.该古城墙的高度是米.
同课章节目录
