第一章二次函数2021-2022学年浙教版九年级数学上册期中复习训练卷(B卷)(Word版含答案)
文档属性
| 名称 | 第一章二次函数2021-2022学年浙教版九年级数学上册期中复习训练卷(B卷)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览


文档简介
2021-2022学年浙教版九年级上册期中复习训练卷(B卷)
第一章:二次函数
一、单选题(共10题,共30分)
1.(2020九上·柯桥期中)函数图象 中,函数 与自变量 的部分对应值如表:
… -1 0 1 2 3 4 …
… 10 5 2 1 2 5 …
二次函数的对称轴是直线( )
A. B. C. D.
2.(2020九上·杭州期中)一条抛物线y=ax2+bx+c的顶点为(2,m),m<0,且与x轴有两个交点,其中一个交点是(5,0),则对a、b、c描述正确的是( )
A. a>0、b<0、c>0 B. a>0、b<0、c<0
C. a<0、b>0、c>0 D. a<0、b>0、c<0
3.(2020九上·柯桥期中)一条抛物线 的顶点为 , ,且与 轴有两个交点,其中一个交点是 ,则对 、 、 描述正确的是( )
A. 、 、 B. 、 、
C. 、 、 D. 、 、
4.(2020九上·越城期中)对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )
A. x≥﹣1 B. x≥0 C. x≤0 D. x≤﹣1
5.(2020九上·越城期中)对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是( )
A. 1 B. 2 C. 0 D. 不能确定
6.(2020九上·越城期中)某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A. 2m B. 3m C. 4m D. 5m
7.(2020九上·杭州期中)二次函数y=x2+px+q,当0≤x≤1时,设此函数最大值为8,最小值为t,w=s﹣t,(s为常数)则w的值( )
A. 与p、q的值都有关 B. 与p无关,但与q有关
C. 与p、q的值都无关 D. 与p有关,但与q无关
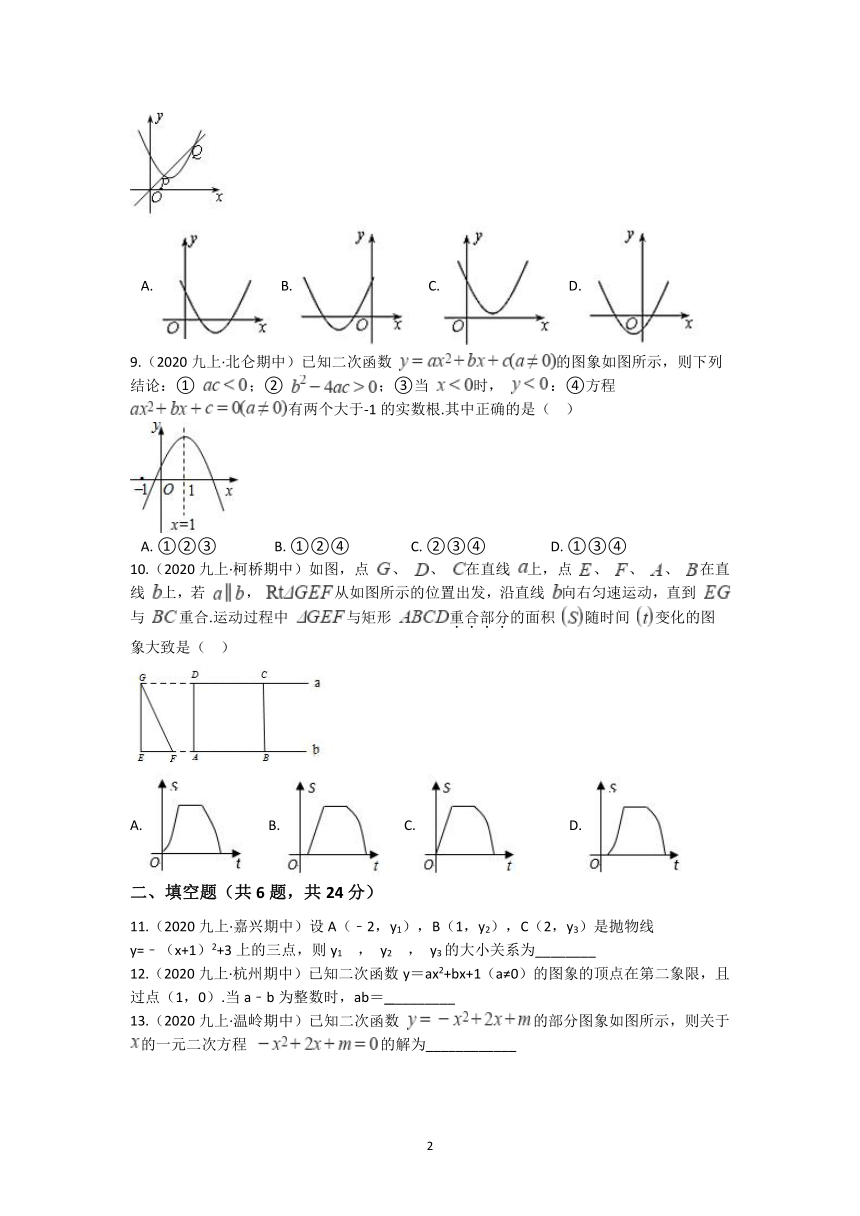
8.(2020九上·越城期中)如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-2)x+c的图象可能是( )
A. B. C. D.
9.(2020九上·北仑期中)已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.(2020九上·柯桥期中)如图,点 、 、 在直线 上,点 、 、 、 在直线 上,若 , 从如图所示的位置出发,沿直线 向右匀速运动,直到 与 重合.运动过程中 与矩形 重合部分的面积 随时间 变化的图象大致是( )
A. B. C. D.
二、填空题(共6题,共24分)
11.(2020九上·嘉兴期中)设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线
y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为________
12.(2020九上·杭州期中)已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a﹣b为整数时,ab= ________
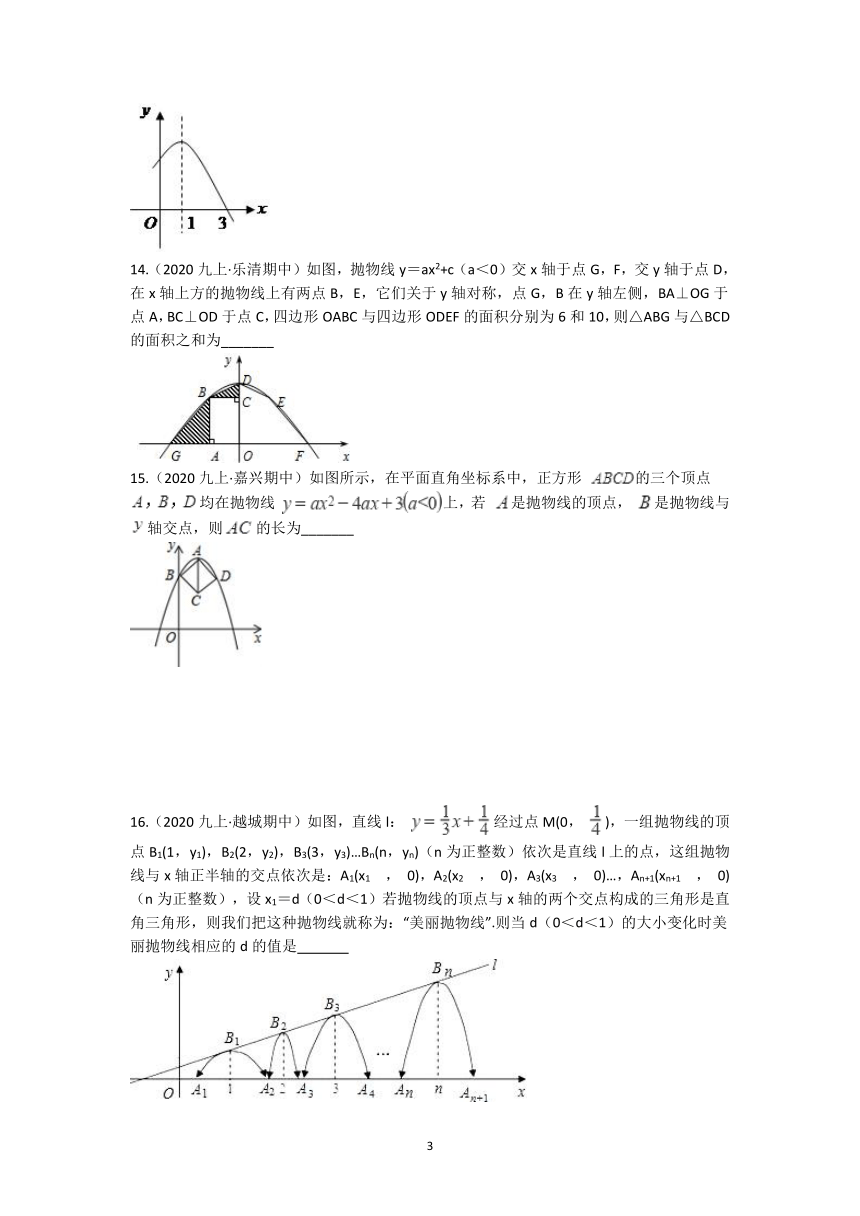
13.(2020九上·温岭期中)已知二次函数 的部分图象如图所示,则关于 的一元二次方程 的解为____________
14.(2020九上·乐清期中)如图,抛物线y=ax2+c(a<0)交x轴于点G,F,交y轴于点D,在x轴上方的抛物线上有两点B,E,它们关于y轴对称,点G,B在y轴左侧,BA⊥OG于点A,BC⊥OD于点C,四边形OABC与四边形ODEF的面积分别为6和10,则△ABG与△BCD的面积之和为_______
15.(2020九上·嘉兴期中)如图所示,在平面直角坐标系中,正方形 的三个顶点 均在抛物线 上,若 是抛物线的顶点, 是抛物线与 轴交点,则的长为_______
16.(2020九上·越城期中)如图,直线l: 经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时美丽抛物线相应的d的值是
三、解答题(共8题,共66分)
17.(6分)(2020九上·杭州期中)已知二次函数y=x2+bx+c过(1,0),(0,﹣3).
(1)求该二次函数的解析式;
(2)若﹣1≤x≤1,求y的取值范围。
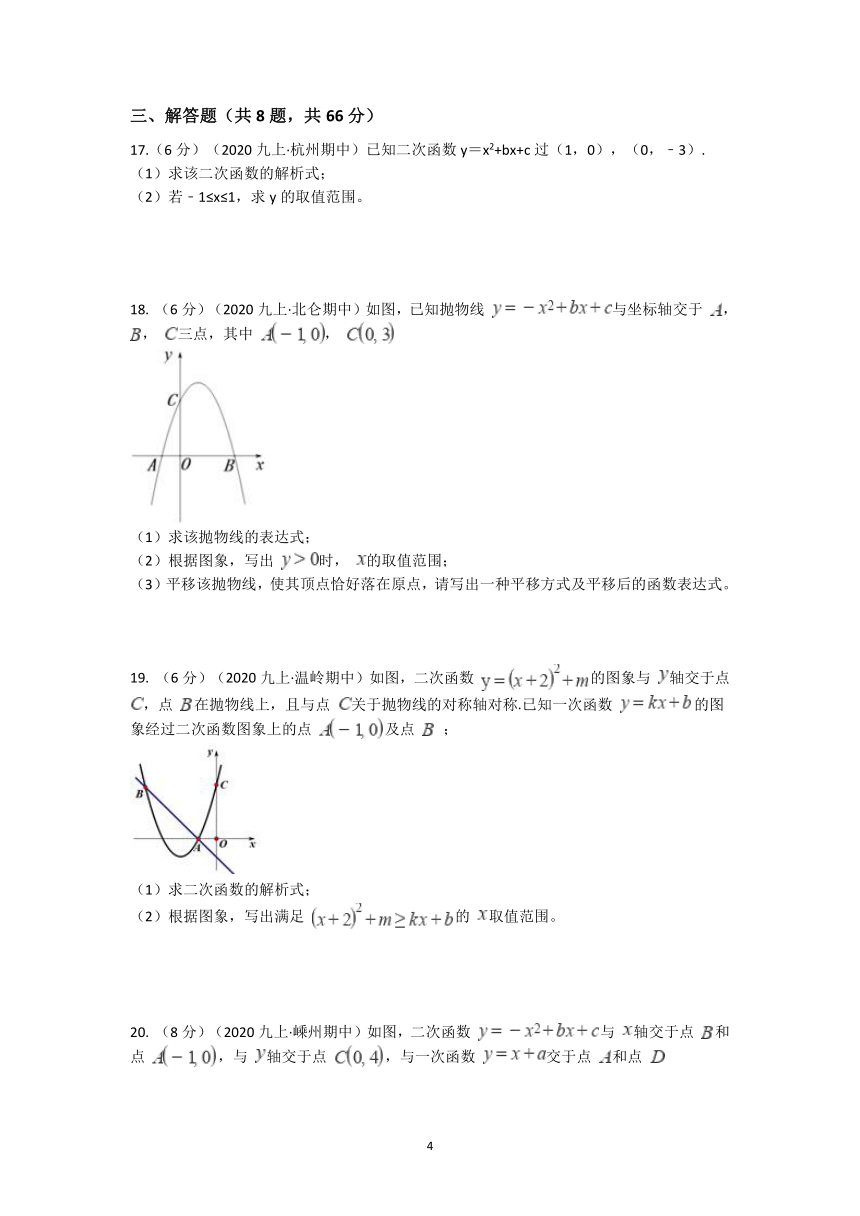
18. (6分)(2020九上·北仑期中)如图,已知抛物线 与坐标轴交于 , , 三点,其中 ,
(1)求该抛物线的表达式;
(2)根据图象,写出 时, 的取值范围;
(3)平移该抛物线,使其顶点恰好落在原点,请写出一种平移方式及平移后的函数表达式。
19. (6分)(2020九上·温岭期中)如图,二次函数 的图象与 轴交于点 ,点 在抛物线上,且与点 关于抛物线的对称轴对称.已知一次函数 的图象经过二次函数图象上的点 及点 ;
(1)求二次函数的解析式;
(2)根据图象,写出满足 的 取值范围。
20. (8分)(2020九上·嵊州期中)如图,二次函数 与 轴交于点 和点 ,与 轴交于点 ,与一次函数 交于点 和点
(1)求出 、 、 的值;
(2)若直线 上方的抛物线存在点 ,可使得 面积最大,求点 的坐标;
(3)点 为线段 上的一个动点,点 到(2)中的点 的距离与到 轴的距离之和记为 ,求 的最小值及此时点 的坐标。
21. (8分)(2020九上·杭州期中)在平面直角坐标系中,设二次函数y1=x2+bx+c,y2=﹣x2+bx﹣c(b,c是实数)
(1)若函数y1的图象经过点(r,g),求证函数y2的图象经过点(﹣r,﹣g)
(2)设函数y1和函数y2的最值分别为m和n;
①若函数y1的图象先向右平移2个单位,再向下平移2个单位得到函数y3 , 若函数y3的最值为k,若k=n,求b,c的值;
②若m=n且函数y1的图象经过点(p,q)和(p+6,q)两点,求q的值。
22. (10分)(2020九上·乐清期中)如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=﹣+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M。
(1)求OD,PM的长(结果均用含k的代数式表示);
(2)当PM=BM时,求该抛物线的表达式;
(3)在点A在整个运动过程中,若存在△ADP是等腰三角形,请求出所有满足条件的k的值。
23. (10分)(2020九上·温岭期中)在平面直角坐标系 中,对于点 和点 ,给出如下定义:若 则称点 为点 的限变点
(1).点 的限变点的坐标是 , 点 的限变点的坐标是
(2).若点 在函数 的图象上,其限变点 的纵坐标 的取值范围是 ,求 的取值范围;
(3).若点 在关于 的二次函数 的图象上,其限变点 的纵坐标 的取值范围是 或 ,其中 令 ,则 关于 的函数表达式及 的取值范围。
24. (12分)(2020九上·越城期中)如图,已知二次函数y=x2+bx+c的图象经过A,B两点,BC⊥x轴于点C, 且点A(﹣1,0),C(4,0),AC=BC
(1)求抛物线的解析式;
(2)点E是线段AB上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F , 当线段EF的长度最大时,求点E的坐标及S△ABF;
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,直接写出所有点P的坐标;若不存在,请说明理由。
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:由表格可得:抛物线的对称轴为: ;
故答案为:C
2.【答案】 B
【解析】【解答】解:由题意得: ,解得 ,
由c﹣4a<0得,﹣5a﹣4a<0,故a>0,则b<0,c<0,
故答案为:B
3.【答案】 B
【解析】【解答】解:由题意得: , 解得 ,
由c 4a<0得, 5a 4a<0,故a>0,则b<0,c<0,
故答案为:B
4.【答案】 D
【解析】【解答】∵y=﹣x2﹣2x﹣2=﹣(x+1)2﹣1,
a=﹣1<0,抛物线开口向下,对称轴为直线x=﹣1,∴当x≤﹣1时,y随x的增大而增大,
故答案为:D
5.【答案】 B
【解析】【解答】由题意可知:函数的零点也就是二次函数y=ax2+bx+c与x轴的交点,
二次函数y=x2﹣mx﹣5,△=(﹣m)2﹣4×1×(﹣5)=m2+20,
∵m2一定为非负数,∴m2+20>0,
∴二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是2
故答案为:B
6.【答案】 B
【解析】【解答】设抛物线的解析式为y=a(x﹣1)2+ ,
把点A(0,10)代入a(x﹣1)2+ ,得a(0﹣1)2+ =10,解得a=﹣ ,
因此抛物线解析式为y=﹣ (x﹣1)2+ ,
当y=0时,解得x1=3,x2=﹣1(不合题意,舍去);即OB=3米.
故答案为:B
7.【答案】 D
【解析】【解答】解:∵二次函数y=x2+px+q=(x+ )2+ ,
∴该抛物线的对称轴为x=﹣ ,且a=1>0,
当x=﹣ <0,∴当x=1时,二次函数有最大值为:1+p+q=8,即p+q=7,
∴当x=0时,二次函数有最小值为:q=t,即t=7﹣p,
当x=﹣ >1,∴当x=0时,二次函数有最大值为:q=8,
∴当x=1时,二次函数有最小值为:1+p+q=t,即t=9+p,
当0≤﹣ < ,此时当x=1时,函数有最大值1+p+q=8,
当x=﹣ 时,函数有最小值q﹣ =t,即t=7﹣p﹣ ,
<﹣ ≤1,当x=0时,函数有最大值q=8,当x=﹣ 时,函数有最小值q﹣ =t,即t=8﹣ ,x=﹣ = ,当x=0或1时.函数有最大值q=8,
当x=﹣ 时,函数有最小值q﹣ =t,即t=8﹣
∵w=s﹣t,∴w的值与p有关,但与q无关,
故答案为:D
8.【答案】 A
【解析】【解答】由图可知一元二次方程ax2+bx+c=2x有两个不等的正实数根
即y=ax2+(b-2)x+c与x轴正半轴有两个交点.
故答案为:A
9.【答案】 B
【解析】【解答】解:①∵图象开口向下,∴a<0,∵图象与y轴交于正半轴,则c>0,∴ac<0,故①正确;
②∵二次函数图象与x轴有两个交点即有两个不相等的实数根,所以,故②正确;
③当x<0时,有部分图象在x的上方,即函数值y不一定小于0,故③错误;
④利用图象与x轴交点都大于-1,故方程 有两个大于-1的实数根,故④正确;
故答案为:B
10.【答案】 D
【解析】【解答】解:根据题意可得:①F、A重合之前没有重叠面积,
②F、A重叠之后到E与A重叠前,设AE=a,EF被重叠部分的长度为(t-a),则重叠部分面积为S= (t-a) (t-a)tan∠EFG= (t-a)2tan∠EFG,∴是二次函数图象;
③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变;
④F与B重合之后,重叠部分的面积等于S=S△EFG- (t-a)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
综上所述,只有D选项图形符合
故答案为:D
二、填空题
11.【答案】 y1 >y2>y3
【解析】【解答】解:∵ y=﹣(x+1)2+3,a=-1<0, ∴当x>-1时,y随x的增大而减小,
∵点 A(﹣2,y1)关于对称轴直线x=-1的对称点的坐标为(0,y1)
∵0<1<2∴ y1 >y2>y3
故答案为:y1 >y2>y3
12.【答案】
【解析】【解答】解:依题意知a<0, ,
故b<0,且b=﹣a﹣1,a﹣b=a﹣(﹣a﹣1)=2a+1,于是﹣1<a<0,
又∵a﹣b为整数,∴2a+1=0,解得,a=﹣ ,
∴b=﹣a﹣1=﹣(﹣ )﹣1=﹣ ,∴ab=(﹣ )×(﹣ )= ,
故答案为:
13.【答案】 -1或3
【解析】【解答】解:观察图象得,二次函数 的部分图象经过(3,0),
∴将(3,0)代入 ,解得:m=3,
将m=3代入 ,即 ,解这个方程可得: ,
故答案为:-1或3
14.【答案】 4
【解析】【解答】解:由于抛物线的对称轴是y轴,根据抛物线的对称性知:
S四边形ODEF=S四边形ODBG=10;
∴S△ABG+S△BCD=S四边形ODBG﹣S四边形OABC=10﹣6=4.
15.【答案】 4
【解析】【解答】解:抛物线的对称轴为直线
当x=0时,y=3∴点B坐标(0,3),∵四边形ABCD是正方形,点A是抛物线顶点, ∴B、D关于对称轴对称,∴点D坐标(4,3) ∴AC=BD=|0-4|=4
故答案为:4
16.【答案】 或
【解析】【解答】直线l: ,
当x=1时,y= ,即:B1(1, ),
当x=2时,y= ,即:B2(2, ),
∵A1(d,0),A2(2﹣d,0),若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,即:1﹣d= ,解得:d= ;
同理:若B2为直角顶点,则A2A3的中点(2,0)到B2的距离与到A3和A2的距离相等,
即:2﹣(2﹣d)= ,解得:d= ;
若B3为直角顶点,求出的d为负数,并且从B3之后的B点,求出的d都为负数;
所以d的值是 或
故答案为: 或
三、解答题
17.【答案】 (1)解:∵二次函数y=x2+bx+c过(1,0),(0,﹣3).
∴ ,解得: ,
则二次函数解析式为y=x2+2x﹣3
(2)解:∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点为(﹣1,﹣4),
把x=1代入y=x2+2x﹣3得,y=0,
故当﹣1≤x≤1时,y的取值范围为﹣4≤y≤0
18.【答案】 (1)解:将点 、点 代入 可得:
,解得:
∴该抛物线的表达式 .
(2)解:将y=0代入解析式 , ,解得:x=﹣1或x=3
∵A(﹣1,0)∴ ,结合图象可知,当 时,
(3)解:∵抛物线的表达式
∴抛物线的对称轴为x=1,将x=1代入解析式可得y=4,∴顶点 ,
∴当抛物线向左平移1个单位长度,向下平移4个单位长度时,顶点恰好落在原点,此时抛物线的表达式为
19.【答案】 (1)解:∵抛物线 经过点A(-1,0),∴ ,∴ ,
∴抛物线解析式为 ;
(2)解:∵抛物线解析式为 ,
∴点C坐标(0,3),∵对称轴 ,B、C关于对称轴对称,∴点B坐标(-4,3),
由图象可知,当 或 ,二次函数 的图象在直线 的上方,∴ 的 取值范围为 或
20.【答案】 (1)解:将 与 分别代入二次函数 ,
得 ,解得 ;将点 代入一次函数 ,
得 ,解得 ,∴ , ,
(2)解:由(1)所求的 , , 的值可得一次函数的解析式为: ,抛物线的解析式为: ,
联立 与 得 ,解得
∴点 的坐标为: ,设点 , 过点 作 轴的垂线1,交 轴于点 ,交 于点 ,则点 的坐标为 ,
过点 作l的垂线,垂足为 ;
∴ , ,
∴
,
当 时,最大值为8,此时点 的坐标为
(3)解:过 作 轴的平行线 ,过 作 轴交 于点 ,过 作 轴于 ,
∵点 的坐标为 ,点 坐标为
∴ ,∴ 平分 ,∴ ,
∴
显然,当 、 、 所在直线与 轴垂直时,最小,
最小值为 .此时点 的横坐标为1,
代入 得 点的坐标为
21.【答案】 (1)解:∵函数y1的图象经过点(r,g), ∴g=r2+br+c,
∴﹣g=﹣r2﹣br﹣c,把x=﹣r代入y2=﹣x2+bx﹣c得,y2=﹣r2﹣br﹣c=﹣g,
∴函数y2的图象经过点(﹣r,﹣g)
(2)解:①函数y1的图象先向右平移2个单位,再向下平移2个单位得到函数y3=(x﹣2)2+b(x﹣2)+c﹣2,即y3=x2+(b﹣2)x+2﹣2b+c,
∵函数y3的最值为k,且k=n,∴ = ,整理得4﹣4b=0,
解得b=1,∴y3=x2﹣x+c,y2=﹣x2+x﹣c,
∴函数y2的图象与函数y3的图象关于x轴对称,∴k=n=0,∴ =0,∴4c=b2=1,
∴c= ;
②∵函数y1和函数y2的最值分别为m和n,∴m= ,n= ,
∵m=n,∴ = ,∴8c=2b2 , 即c= ,∴y1=x2+bx+ =(x+ )2 ,
∵函数y1的图象经过点(p,q)和(p+6,q)两点,
∴﹣ = =p+3,∴y1=(x﹣p﹣3)2 ,∴q=(p﹣p﹣3)2=9
22.【答案】 (1)解:把x=0,代入y=﹣ +3x+k, ∴y=k.∴OD=k.
∵ = =k+3,∴PM=k+3;
解:由抛物线的表达式知,其对称轴为x=2,
∴OM=2,BM=OB﹣OM=2k+3﹣2=2k+1.
又∵PM=k+3,PM=BM,∴k+3=2k+1,解得k=2,∴该抛物线的表达式为y=﹣ +3x+2;
(3)解:①当点P在矩形AOBC外部时,如图1,
过P作PK⊥OA于点K,当AD=AP时,
∵AD=AO﹣DO=2k﹣k=k,∴AD=AP=k,KA=KO﹣AO=PM﹣AO=k+3﹣2k=3﹣k
KP=OM=2,在Rt△KAP中,KA2+KP2=AP2
∴(3﹣k)2+22=k2 , 解得k=
②当点P在矩形AOBC内部时,当PD=AP时,过P作PH⊥OA于H,
AD=k,HD= k,HO=DO+HD= ,
又∵HO=PM=k+3,∴ =k+3,解得k=6.
当DP=DA时,过D作PQ⊥PM于Q,PQ=PM﹣QM=PM﹣OD=k+3﹣k=3
DQ=OM=2,DP=DA=k,
在Rt△DQP中,DP= = =
∴k=PD= ,故k= 或6或
23.【答案】 (1)(2,3);(-2,-5)
(2)解:如图1:
由得 图象上的点 的限变点在函数 的图象上,显然
当 时, 取最大值,当 时, ,则 (x≤1),故舍去
当 时, 或 ,则 或
因为 ,结合图象,可得 的取值范围是 ;
(3)解:∵ ,∴顶点坐标为
①若 ,如图2:当 时,点 的纵坐标 满足 ,则 ,与题意不符
②若 ,如图3:当 时,点 的纵坐标 满足 ,则 ,则
当 时,点 的纵坐标 满足 ,则 ,即 ;
∴ ,即
当 时, ,∴ 的取值范围是 .
24.【答案】 (1)解:∵点A(﹣1,0),C(4,0), ∴AC=5,OC=4,
∵AC=BC=5,∴B(4,5),
把A(﹣1,0)和B(4,5)代入二次函数y=x2+bx+c中得:
,解得: ,
∴二次函数的解析式为:y=x2﹣2x﹣3
(2)解:如图1,∵直线AB经过点A(﹣1,0),B(4,5),
设直线AB的解析式为y=kx+b,
∴ ,解得: ,
∴直线AB的解析式为:y=x+1,
∵二次函数y=x2﹣2x﹣3,∴设点E(t,t+1),则F(t,t2﹣2t﹣3),
∴EF=(t+1)﹣(t2﹣2t﹣3)=﹣(t﹣ )2+
∴当t= 时,EF的最大值为 ,∴点E的坐标为( , ),
∴S△ABF= = =
(3)解:存在,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴对称轴为直线x=1,
设P(1,m),分三种情况:
①点B为直角顶点时,由勾股定理得: ,
∴(4﹣1)2+(m﹣5)2+(4+1)2+52=(1+1)2+m2 , 解得:m=8,∴P(1,8);
②点A为直角顶点时,由勾股定理得:
∴(1+1)2+m2+(4+1)2+52=(4﹣1)2+(m﹣52 , 解得:m=﹣2,∴P(1,﹣2);
③点P为直角顶点时,由勾股定理得: ,
∴(4﹣1)2+(m﹣5)2+(1+1)2+m2=(4+1)2+52 ,解得:m=6或m=﹣1,
∴P(1,6)或P(1,﹣1)
综上,点P的坐标为(1,8)或(1,﹣2)或(1,6)或(1,﹣1)
第一章:二次函数
一、单选题(共10题,共30分)
1.(2020九上·柯桥期中)函数图象 中,函数 与自变量 的部分对应值如表:
… -1 0 1 2 3 4 …
… 10 5 2 1 2 5 …
二次函数的对称轴是直线( )
A. B. C. D.
2.(2020九上·杭州期中)一条抛物线y=ax2+bx+c的顶点为(2,m),m<0,且与x轴有两个交点,其中一个交点是(5,0),则对a、b、c描述正确的是( )
A. a>0、b<0、c>0 B. a>0、b<0、c<0
C. a<0、b>0、c>0 D. a<0、b>0、c<0
3.(2020九上·柯桥期中)一条抛物线 的顶点为 , ,且与 轴有两个交点,其中一个交点是 ,则对 、 、 描述正确的是( )
A. 、 、 B. 、 、
C. 、 、 D. 、 、
4.(2020九上·越城期中)对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )
A. x≥﹣1 B. x≥0 C. x≤0 D. x≤﹣1
5.(2020九上·越城期中)对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是( )
A. 1 B. 2 C. 0 D. 不能确定
6.(2020九上·越城期中)某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A. 2m B. 3m C. 4m D. 5m
7.(2020九上·杭州期中)二次函数y=x2+px+q,当0≤x≤1时,设此函数最大值为8,最小值为t,w=s﹣t,(s为常数)则w的值( )
A. 与p、q的值都有关 B. 与p无关,但与q有关
C. 与p、q的值都无关 D. 与p有关,但与q无关
8.(2020九上·越城期中)如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-2)x+c的图象可能是( )
A. B. C. D.
9.(2020九上·北仑期中)已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
10.(2020九上·柯桥期中)如图,点 、 、 在直线 上,点 、 、 、 在直线 上,若 , 从如图所示的位置出发,沿直线 向右匀速运动,直到 与 重合.运动过程中 与矩形 重合部分的面积 随时间 变化的图象大致是( )
A. B. C. D.
二、填空题(共6题,共24分)
11.(2020九上·嘉兴期中)设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线
y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为________
12.(2020九上·杭州期中)已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a﹣b为整数时,ab= ________
13.(2020九上·温岭期中)已知二次函数 的部分图象如图所示,则关于 的一元二次方程 的解为____________
14.(2020九上·乐清期中)如图,抛物线y=ax2+c(a<0)交x轴于点G,F,交y轴于点D,在x轴上方的抛物线上有两点B,E,它们关于y轴对称,点G,B在y轴左侧,BA⊥OG于点A,BC⊥OD于点C,四边形OABC与四边形ODEF的面积分别为6和10,则△ABG与△BCD的面积之和为_______
15.(2020九上·嘉兴期中)如图所示,在平面直角坐标系中,正方形 的三个顶点 均在抛物线 上,若 是抛物线的顶点, 是抛物线与 轴交点,则的长为_______
16.(2020九上·越城期中)如图,直线l: 经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时美丽抛物线相应的d的值是
三、解答题(共8题,共66分)
17.(6分)(2020九上·杭州期中)已知二次函数y=x2+bx+c过(1,0),(0,﹣3).
(1)求该二次函数的解析式;
(2)若﹣1≤x≤1,求y的取值范围。
18. (6分)(2020九上·北仑期中)如图,已知抛物线 与坐标轴交于 , , 三点,其中 ,
(1)求该抛物线的表达式;
(2)根据图象,写出 时, 的取值范围;
(3)平移该抛物线,使其顶点恰好落在原点,请写出一种平移方式及平移后的函数表达式。
19. (6分)(2020九上·温岭期中)如图,二次函数 的图象与 轴交于点 ,点 在抛物线上,且与点 关于抛物线的对称轴对称.已知一次函数 的图象经过二次函数图象上的点 及点 ;
(1)求二次函数的解析式;
(2)根据图象,写出满足 的 取值范围。
20. (8分)(2020九上·嵊州期中)如图,二次函数 与 轴交于点 和点 ,与 轴交于点 ,与一次函数 交于点 和点
(1)求出 、 、 的值;
(2)若直线 上方的抛物线存在点 ,可使得 面积最大,求点 的坐标;
(3)点 为线段 上的一个动点,点 到(2)中的点 的距离与到 轴的距离之和记为 ,求 的最小值及此时点 的坐标。
21. (8分)(2020九上·杭州期中)在平面直角坐标系中,设二次函数y1=x2+bx+c,y2=﹣x2+bx﹣c(b,c是实数)
(1)若函数y1的图象经过点(r,g),求证函数y2的图象经过点(﹣r,﹣g)
(2)设函数y1和函数y2的最值分别为m和n;
①若函数y1的图象先向右平移2个单位,再向下平移2个单位得到函数y3 , 若函数y3的最值为k,若k=n,求b,c的值;
②若m=n且函数y1的图象经过点(p,q)和(p+6,q)两点,求q的值。
22. (10分)(2020九上·乐清期中)如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=﹣+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M。
(1)求OD,PM的长(结果均用含k的代数式表示);
(2)当PM=BM时,求该抛物线的表达式;
(3)在点A在整个运动过程中,若存在△ADP是等腰三角形,请求出所有满足条件的k的值。
23. (10分)(2020九上·温岭期中)在平面直角坐标系 中,对于点 和点 ,给出如下定义:若 则称点 为点 的限变点
(1).点 的限变点的坐标是 , 点 的限变点的坐标是
(2).若点 在函数 的图象上,其限变点 的纵坐标 的取值范围是 ,求 的取值范围;
(3).若点 在关于 的二次函数 的图象上,其限变点 的纵坐标 的取值范围是 或 ,其中 令 ,则 关于 的函数表达式及 的取值范围。
24. (12分)(2020九上·越城期中)如图,已知二次函数y=x2+bx+c的图象经过A,B两点,BC⊥x轴于点C, 且点A(﹣1,0),C(4,0),AC=BC
(1)求抛物线的解析式;
(2)点E是线段AB上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F , 当线段EF的长度最大时,求点E的坐标及S△ABF;
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,直接写出所有点P的坐标;若不存在,请说明理由。
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:由表格可得:抛物线的对称轴为: ;
故答案为:C
2.【答案】 B
【解析】【解答】解:由题意得: ,解得 ,
由c﹣4a<0得,﹣5a﹣4a<0,故a>0,则b<0,c<0,
故答案为:B
3.【答案】 B
【解析】【解答】解:由题意得: , 解得 ,
由c 4a<0得, 5a 4a<0,故a>0,则b<0,c<0,
故答案为:B
4.【答案】 D
【解析】【解答】∵y=﹣x2﹣2x﹣2=﹣(x+1)2﹣1,
a=﹣1<0,抛物线开口向下,对称轴为直线x=﹣1,∴当x≤﹣1时,y随x的增大而增大,
故答案为:D
5.【答案】 B
【解析】【解答】由题意可知:函数的零点也就是二次函数y=ax2+bx+c与x轴的交点,
二次函数y=x2﹣mx﹣5,△=(﹣m)2﹣4×1×(﹣5)=m2+20,
∵m2一定为非负数,∴m2+20>0,
∴二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是2
故答案为:B
6.【答案】 B
【解析】【解答】设抛物线的解析式为y=a(x﹣1)2+ ,
把点A(0,10)代入a(x﹣1)2+ ,得a(0﹣1)2+ =10,解得a=﹣ ,
因此抛物线解析式为y=﹣ (x﹣1)2+ ,
当y=0时,解得x1=3,x2=﹣1(不合题意,舍去);即OB=3米.
故答案为:B
7.【答案】 D
【解析】【解答】解:∵二次函数y=x2+px+q=(x+ )2+ ,
∴该抛物线的对称轴为x=﹣ ,且a=1>0,
当x=﹣ <0,∴当x=1时,二次函数有最大值为:1+p+q=8,即p+q=7,
∴当x=0时,二次函数有最小值为:q=t,即t=7﹣p,
当x=﹣ >1,∴当x=0时,二次函数有最大值为:q=8,
∴当x=1时,二次函数有最小值为:1+p+q=t,即t=9+p,
当0≤﹣ < ,此时当x=1时,函数有最大值1+p+q=8,
当x=﹣ 时,函数有最小值q﹣ =t,即t=7﹣p﹣ ,
<﹣ ≤1,当x=0时,函数有最大值q=8,当x=﹣ 时,函数有最小值q﹣ =t,即t=8﹣ ,x=﹣ = ,当x=0或1时.函数有最大值q=8,
当x=﹣ 时,函数有最小值q﹣ =t,即t=8﹣
∵w=s﹣t,∴w的值与p有关,但与q无关,
故答案为:D
8.【答案】 A
【解析】【解答】由图可知一元二次方程ax2+bx+c=2x有两个不等的正实数根
即y=ax2+(b-2)x+c与x轴正半轴有两个交点.
故答案为:A
9.【答案】 B
【解析】【解答】解:①∵图象开口向下,∴a<0,∵图象与y轴交于正半轴,则c>0,∴ac<0,故①正确;
②∵二次函数图象与x轴有两个交点即有两个不相等的实数根,所以,故②正确;
③当x<0时,有部分图象在x的上方,即函数值y不一定小于0,故③错误;
④利用图象与x轴交点都大于-1,故方程 有两个大于-1的实数根,故④正确;
故答案为:B
10.【答案】 D
【解析】【解答】解:根据题意可得:①F、A重合之前没有重叠面积,
②F、A重叠之后到E与A重叠前,设AE=a,EF被重叠部分的长度为(t-a),则重叠部分面积为S= (t-a) (t-a)tan∠EFG= (t-a)2tan∠EFG,∴是二次函数图象;
③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变;
④F与B重合之后,重叠部分的面积等于S=S△EFG- (t-a)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
综上所述,只有D选项图形符合
故答案为:D
二、填空题
11.【答案】 y1 >y2>y3
【解析】【解答】解:∵ y=﹣(x+1)2+3,a=-1<0, ∴当x>-1时,y随x的增大而减小,
∵点 A(﹣2,y1)关于对称轴直线x=-1的对称点的坐标为(0,y1)
∵0<1<2∴ y1 >y2>y3
故答案为:y1 >y2>y3
12.【答案】
【解析】【解答】解:依题意知a<0, ,
故b<0,且b=﹣a﹣1,a﹣b=a﹣(﹣a﹣1)=2a+1,于是﹣1<a<0,
又∵a﹣b为整数,∴2a+1=0,解得,a=﹣ ,
∴b=﹣a﹣1=﹣(﹣ )﹣1=﹣ ,∴ab=(﹣ )×(﹣ )= ,
故答案为:
13.【答案】 -1或3
【解析】【解答】解:观察图象得,二次函数 的部分图象经过(3,0),
∴将(3,0)代入 ,解得:m=3,
将m=3代入 ,即 ,解这个方程可得: ,
故答案为:-1或3
14.【答案】 4
【解析】【解答】解:由于抛物线的对称轴是y轴,根据抛物线的对称性知:
S四边形ODEF=S四边形ODBG=10;
∴S△ABG+S△BCD=S四边形ODBG﹣S四边形OABC=10﹣6=4.
15.【答案】 4
【解析】【解答】解:抛物线的对称轴为直线
当x=0时,y=3∴点B坐标(0,3),∵四边形ABCD是正方形,点A是抛物线顶点, ∴B、D关于对称轴对称,∴点D坐标(4,3) ∴AC=BD=|0-4|=4
故答案为:4
16.【答案】 或
【解析】【解答】直线l: ,
当x=1时,y= ,即:B1(1, ),
当x=2时,y= ,即:B2(2, ),
∵A1(d,0),A2(2﹣d,0),若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,即:1﹣d= ,解得:d= ;
同理:若B2为直角顶点,则A2A3的中点(2,0)到B2的距离与到A3和A2的距离相等,
即:2﹣(2﹣d)= ,解得:d= ;
若B3为直角顶点,求出的d为负数,并且从B3之后的B点,求出的d都为负数;
所以d的值是 或
故答案为: 或
三、解答题
17.【答案】 (1)解:∵二次函数y=x2+bx+c过(1,0),(0,﹣3).
∴ ,解得: ,
则二次函数解析式为y=x2+2x﹣3
(2)解:∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点为(﹣1,﹣4),
把x=1代入y=x2+2x﹣3得,y=0,
故当﹣1≤x≤1时,y的取值范围为﹣4≤y≤0
18.【答案】 (1)解:将点 、点 代入 可得:
,解得:
∴该抛物线的表达式 .
(2)解:将y=0代入解析式 , ,解得:x=﹣1或x=3
∵A(﹣1,0)∴ ,结合图象可知,当 时,
(3)解:∵抛物线的表达式
∴抛物线的对称轴为x=1,将x=1代入解析式可得y=4,∴顶点 ,
∴当抛物线向左平移1个单位长度,向下平移4个单位长度时,顶点恰好落在原点,此时抛物线的表达式为
19.【答案】 (1)解:∵抛物线 经过点A(-1,0),∴ ,∴ ,
∴抛物线解析式为 ;
(2)解:∵抛物线解析式为 ,
∴点C坐标(0,3),∵对称轴 ,B、C关于对称轴对称,∴点B坐标(-4,3),
由图象可知,当 或 ,二次函数 的图象在直线 的上方,∴ 的 取值范围为 或
20.【答案】 (1)解:将 与 分别代入二次函数 ,
得 ,解得 ;将点 代入一次函数 ,
得 ,解得 ,∴ , ,
(2)解:由(1)所求的 , , 的值可得一次函数的解析式为: ,抛物线的解析式为: ,
联立 与 得 ,解得
∴点 的坐标为: ,设点 , 过点 作 轴的垂线1,交 轴于点 ,交 于点 ,则点 的坐标为 ,
过点 作l的垂线,垂足为 ;
∴ , ,
∴
,
当 时,最大值为8,此时点 的坐标为
(3)解:过 作 轴的平行线 ,过 作 轴交 于点 ,过 作 轴于 ,
∵点 的坐标为 ,点 坐标为
∴ ,∴ 平分 ,∴ ,
∴
显然,当 、 、 所在直线与 轴垂直时,最小,
最小值为 .此时点 的横坐标为1,
代入 得 点的坐标为
21.【答案】 (1)解:∵函数y1的图象经过点(r,g), ∴g=r2+br+c,
∴﹣g=﹣r2﹣br﹣c,把x=﹣r代入y2=﹣x2+bx﹣c得,y2=﹣r2﹣br﹣c=﹣g,
∴函数y2的图象经过点(﹣r,﹣g)
(2)解:①函数y1的图象先向右平移2个单位,再向下平移2个单位得到函数y3=(x﹣2)2+b(x﹣2)+c﹣2,即y3=x2+(b﹣2)x+2﹣2b+c,
∵函数y3的最值为k,且k=n,∴ = ,整理得4﹣4b=0,
解得b=1,∴y3=x2﹣x+c,y2=﹣x2+x﹣c,
∴函数y2的图象与函数y3的图象关于x轴对称,∴k=n=0,∴ =0,∴4c=b2=1,
∴c= ;
②∵函数y1和函数y2的最值分别为m和n,∴m= ,n= ,
∵m=n,∴ = ,∴8c=2b2 , 即c= ,∴y1=x2+bx+ =(x+ )2 ,
∵函数y1的图象经过点(p,q)和(p+6,q)两点,
∴﹣ = =p+3,∴y1=(x﹣p﹣3)2 ,∴q=(p﹣p﹣3)2=9
22.【答案】 (1)解:把x=0,代入y=﹣ +3x+k, ∴y=k.∴OD=k.
∵ = =k+3,∴PM=k+3;
解:由抛物线的表达式知,其对称轴为x=2,
∴OM=2,BM=OB﹣OM=2k+3﹣2=2k+1.
又∵PM=k+3,PM=BM,∴k+3=2k+1,解得k=2,∴该抛物线的表达式为y=﹣ +3x+2;
(3)解:①当点P在矩形AOBC外部时,如图1,
过P作PK⊥OA于点K,当AD=AP时,
∵AD=AO﹣DO=2k﹣k=k,∴AD=AP=k,KA=KO﹣AO=PM﹣AO=k+3﹣2k=3﹣k
KP=OM=2,在Rt△KAP中,KA2+KP2=AP2
∴(3﹣k)2+22=k2 , 解得k=
②当点P在矩形AOBC内部时,当PD=AP时,过P作PH⊥OA于H,
AD=k,HD= k,HO=DO+HD= ,
又∵HO=PM=k+3,∴ =k+3,解得k=6.
当DP=DA时,过D作PQ⊥PM于Q,PQ=PM﹣QM=PM﹣OD=k+3﹣k=3
DQ=OM=2,DP=DA=k,
在Rt△DQP中,DP= = =
∴k=PD= ,故k= 或6或
23.【答案】 (1)(2,3);(-2,-5)
(2)解:如图1:
由得 图象上的点 的限变点在函数 的图象上,显然
当 时, 取最大值,当 时, ,则 (x≤1),故舍去
当 时, 或 ,则 或
因为 ,结合图象,可得 的取值范围是 ;
(3)解:∵ ,∴顶点坐标为
①若 ,如图2:当 时,点 的纵坐标 满足 ,则 ,与题意不符
②若 ,如图3:当 时,点 的纵坐标 满足 ,则 ,则
当 时,点 的纵坐标 满足 ,则 ,即 ;
∴ ,即
当 时, ,∴ 的取值范围是 .
24.【答案】 (1)解:∵点A(﹣1,0),C(4,0), ∴AC=5,OC=4,
∵AC=BC=5,∴B(4,5),
把A(﹣1,0)和B(4,5)代入二次函数y=x2+bx+c中得:
,解得: ,
∴二次函数的解析式为:y=x2﹣2x﹣3
(2)解:如图1,∵直线AB经过点A(﹣1,0),B(4,5),
设直线AB的解析式为y=kx+b,
∴ ,解得: ,
∴直线AB的解析式为:y=x+1,
∵二次函数y=x2﹣2x﹣3,∴设点E(t,t+1),则F(t,t2﹣2t﹣3),
∴EF=(t+1)﹣(t2﹣2t﹣3)=﹣(t﹣ )2+
∴当t= 时,EF的最大值为 ,∴点E的坐标为( , ),
∴S△ABF= = =
(3)解:存在,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴对称轴为直线x=1,
设P(1,m),分三种情况:
①点B为直角顶点时,由勾股定理得: ,
∴(4﹣1)2+(m﹣5)2+(4+1)2+52=(1+1)2+m2 , 解得:m=8,∴P(1,8);
②点A为直角顶点时,由勾股定理得:
∴(1+1)2+m2+(4+1)2+52=(4﹣1)2+(m﹣52 , 解得:m=﹣2,∴P(1,﹣2);
③点P为直角顶点时,由勾股定理得: ,
∴(4﹣1)2+(m﹣5)2+(1+1)2+m2=(4+1)2+52 ,解得:m=6或m=﹣1,
∴P(1,6)或P(1,﹣1)
综上,点P的坐标为(1,8)或(1,﹣2)或(1,6)或(1,﹣1)
同课章节目录
