4.2由平行线截得的比例线段 达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.2由平行线截得的比例线段 达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 383.5KB | ||
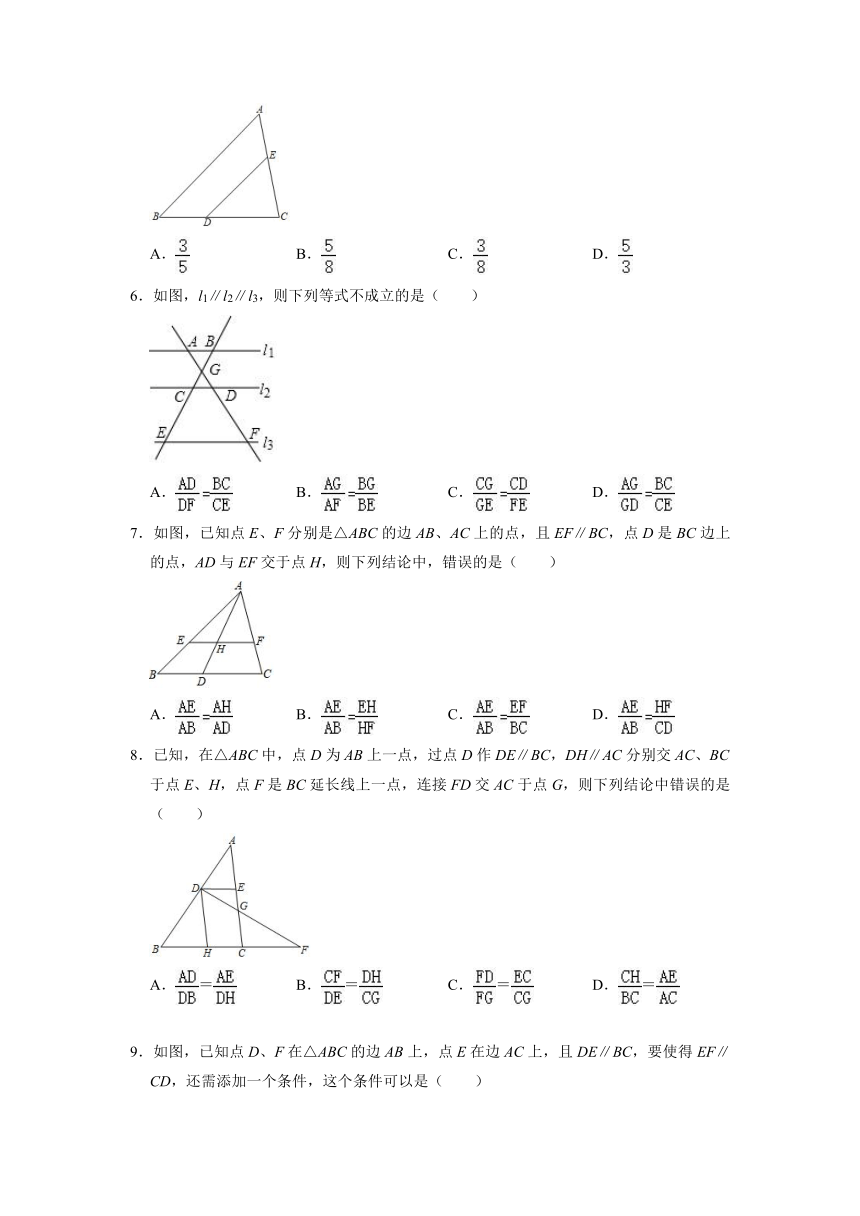
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 10:25:32 | ||
图片预览

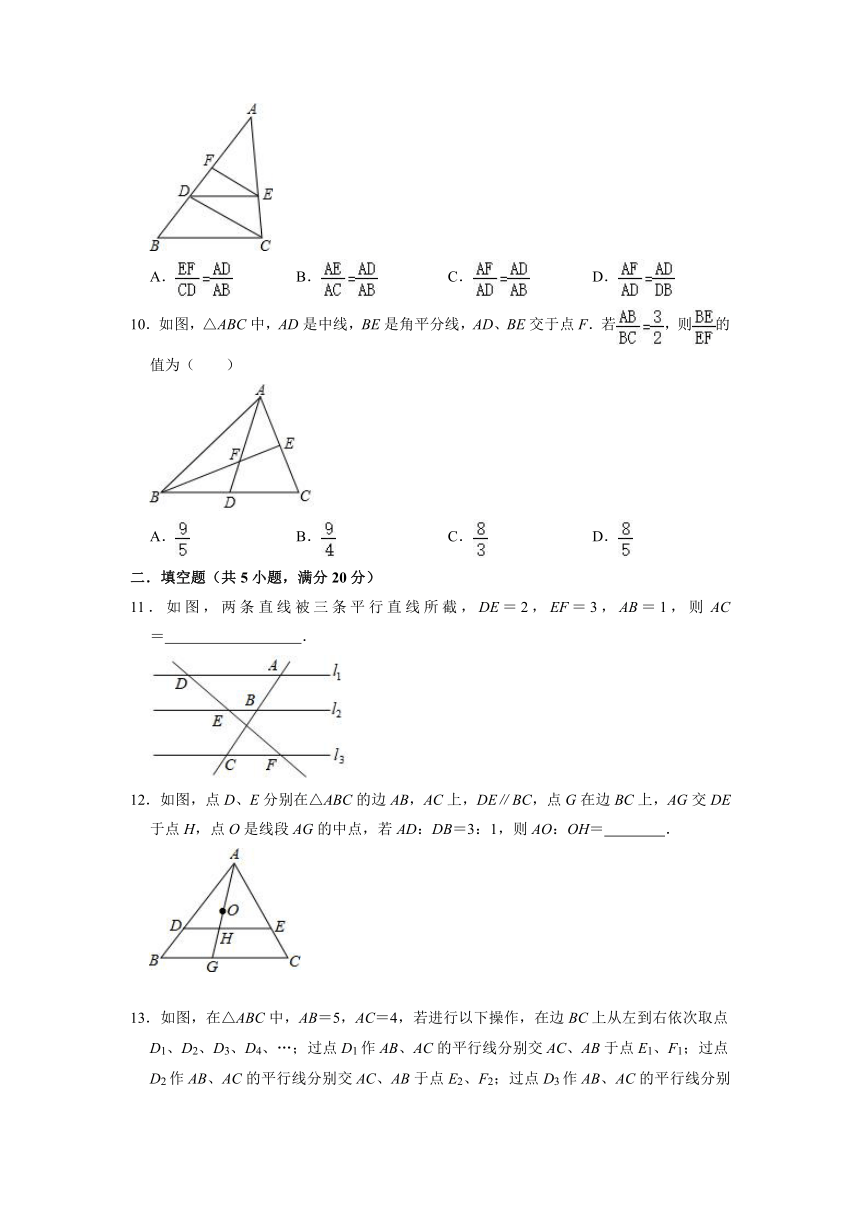

文档简介
2021-2022学年浙教版九年级数学上册《4.2由平行线截得的比例线段》达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,已知点D为△ABC边AB上一点,AD:AB=2:3,过点D作BC的平行线交AC于点E,若AE=6,则EC的长度是( )
A.1 B.2 C.3 D.4
2.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
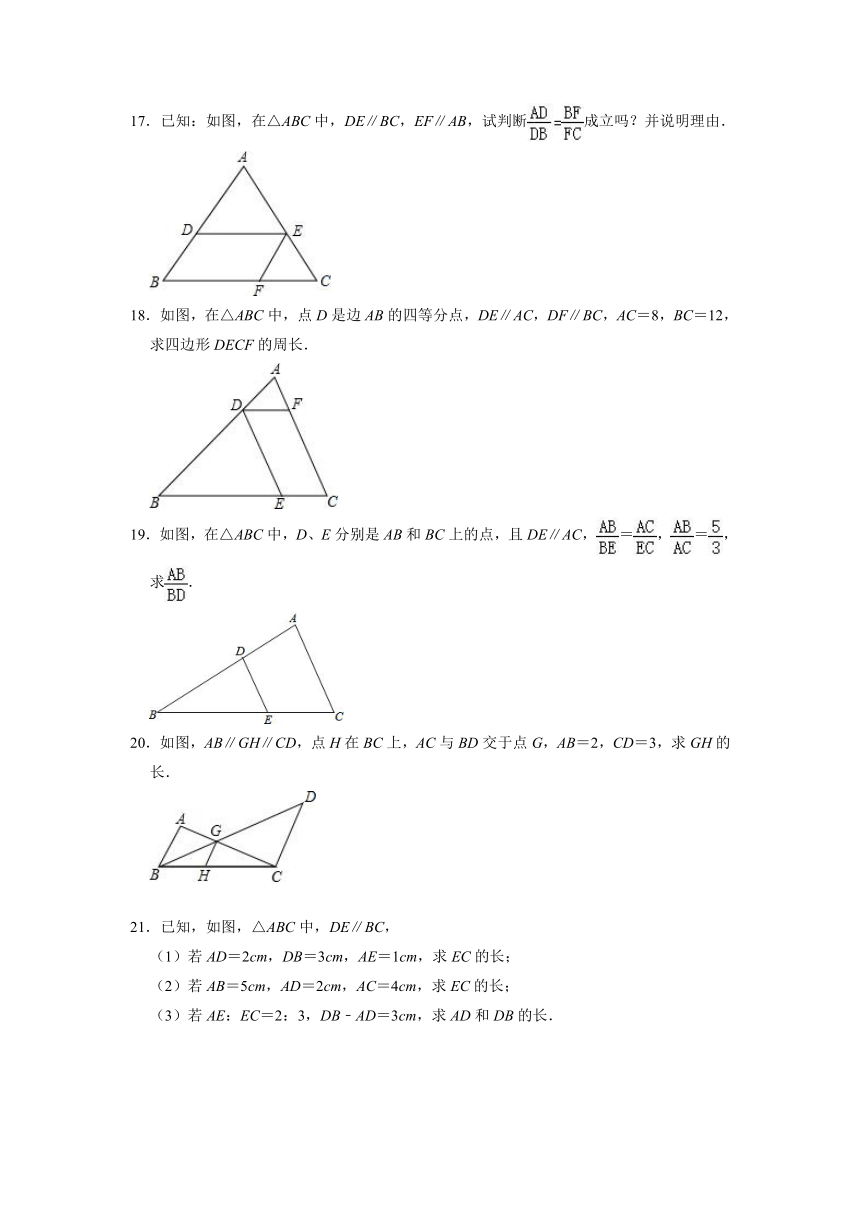
3.如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F.若=,则的值为( )
A. B. C. D.
4.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
5.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
6.如图,l1∥l2∥l3,则下列等式不成立的是( )
A. B. C. D.
7.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
8.已知,在△ABC中,点D为AB上一点,过点D作DE∥BC,DH∥AC分别交AC、BC于点E、H,点F是BC延长线上一点,连接FD交AC于点G,则下列结论中错误的是( )
A.= B.= C.= D.=
9.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
10.如图,△ABC中,AD是中线,BE是角平分线,AD、BE交于点F.若,则的值为( )
A. B. C. D.
二.填空题(共5小题,满分20分)
11.如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
12.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
13.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
14.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF:FD:DB= .
15.如图l1∥l2∥l3,若,DF=10,则DE= .
三.解答题(共8小题,满分60分)
16.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
17.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
18.如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
19.如图,在△ABC中,D、E分别是AB和BC上的点,且DE∥AC,=,=,求.
20.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
21.已知,如图,△ABC中,DE∥BC,
(1)若AD=2cm,DB=3cm,AE=1cm,求EC的长;
(2)若AB=5cm,AD=2cm,AC=4cm,求EC的长;
(3)若AE:EC=2:3,DB﹣AD=3cm,求AD和DB的长.
22.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
23.如图,直线a∥b∥c,直线m,n相交于点O,且分别与直线a,b,c的相交于点A,B,C和点D,E,F,已知OA=3,OB=4,BC=6,EF=5,求DO的长度.
参考答案与
一.选择题(共10小题,满分40分)
1.解:∵DE∥BC,
∴=,
∴=,
∴AC=9,
∴EC=AC﹣AE=9﹣6=3,
故选:C.
2.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
3.解:∵直线l1∥l2∥l3,
∴,
∵,DF=DE+EF.
∴,
故选:D.
4.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
5.解:∵DE∥AB,
∴,
故选:D.
6.解:∵l1∥l2∥l3,
∴,,,,
故选:D.
7.解:∵EF∥BC,
∴=,=,==,
∴选项A,C,D正确,
故选:B.
8.解:∵DE∥BC,DH∥AC,
∴四边形DECH是平行四边形,
∴DH=CE,DE=CH,
∵DE∥BC,
∴==,故选项A正确,不符合题意,
∵DH∥CG,
∴==,故C正确,不符合题意,
∵DE∥BC,
∴=,
∴=,故D正确,不符合题意,
故选:B.
9.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
10.解:如图,过点E作EM⊥AB于M,EN⊥BC于N,作ET∥CB交AD于T.
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN,
∴==,
∴=,
∴=,
∵ET∥CD,
∴==,
∵CD=BD,
∴=,
∴==,
∴=,
∴=,
故选:C.
二.填空题(共5小题,满分20分)
11.解:∵l1∥l2∥l1,
∴=,
∴=,
∴BC=,
∴AC=AB+BC=1+=,
故答案为:.
12.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
13.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
14.解:∵EF∥CD,AE=2EC,
∴==2,
∵DE∥BC,
∴==2,
设DF=m,则AF=2m,AD=3m,DB=m,
∴AF:DF:DB=2m:m:m=4:2:3.
故答案为:4:2:3.
15.解:∵l1∥l2∥l3,,
∴==,
∵DF=10,
∴=,
解得:DE=6,
故答案为:6.
三.解答题(共8小题,满分60分)
16.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
17.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
18.解:∵DE∥AC,DF∥BC,
∴四边形DFCE是平行四边形,
∴DE=FC,DF=EC
∵DF∥BC,
∴△ADF∽△ABC,
∴===,
∵AC=8,BC=12,
∴AF=2,DF=3
∴FC=AC﹣AF=8﹣2=6,
∴DE=FC=6,DF=EC=3
∴四边形DECF的周长是DF+CF+CE+DE=3+6+3+6=18.
答:四边形DECF的周长是18.
19.解:
∵=,
∴=,
∵DE∥AC,
∴,
∴.
20.解:∵AB∥CH∥CD,
∴△CGH∽△ABC,△BGH∽△BCD,
∴,,
∴+=+=1,
∵AB=2,CD=3,
∴=1,
∴GH=.
21.解:(1)∵DE∥BC,
∴=,即=,
∴EC=cm;
(2)∵DE∥BC,
∴=,即=,
∴AE=cm,
∴EC=AC﹣AE=4﹣=(cm);
(3)∵DE∥BC,
∴==,
∴DB=AD,
∵DB﹣AD=3cm,
∴AD﹣AD=3cm,解得AD=6cm,
∴DB=×6=9cm.
22.解:∵a∥b∥c,
∴,
即,
解得:EF=.
23.解:∵a∥b∥c,
∴,
∴,
∴DE=,
∵a∥b∥c,
∴,
∴,
∴DO=.
一.选择题(共10小题,满分40分)
1.如图,已知点D为△ABC边AB上一点,AD:AB=2:3,过点D作BC的平行线交AC于点E,若AE=6,则EC的长度是( )
A.1 B.2 C.3 D.4
2.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
3.如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F.若=,则的值为( )
A. B. C. D.
4.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
5.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
6.如图,l1∥l2∥l3,则下列等式不成立的是( )
A. B. C. D.
7.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
8.已知,在△ABC中,点D为AB上一点,过点D作DE∥BC,DH∥AC分别交AC、BC于点E、H,点F是BC延长线上一点,连接FD交AC于点G,则下列结论中错误的是( )
A.= B.= C.= D.=
9.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
10.如图,△ABC中,AD是中线,BE是角平分线,AD、BE交于点F.若,则的值为( )
A. B. C. D.
二.填空题(共5小题,满分20分)
11.如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
12.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
13.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
14.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF:FD:DB= .
15.如图l1∥l2∥l3,若,DF=10,则DE= .
三.解答题(共8小题,满分60分)
16.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
17.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
18.如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
19.如图,在△ABC中,D、E分别是AB和BC上的点,且DE∥AC,=,=,求.
20.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
21.已知,如图,△ABC中,DE∥BC,
(1)若AD=2cm,DB=3cm,AE=1cm,求EC的长;
(2)若AB=5cm,AD=2cm,AC=4cm,求EC的长;
(3)若AE:EC=2:3,DB﹣AD=3cm,求AD和DB的长.
22.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
23.如图,直线a∥b∥c,直线m,n相交于点O,且分别与直线a,b,c的相交于点A,B,C和点D,E,F,已知OA=3,OB=4,BC=6,EF=5,求DO的长度.
参考答案与
一.选择题(共10小题,满分40分)
1.解:∵DE∥BC,
∴=,
∴=,
∴AC=9,
∴EC=AC﹣AE=9﹣6=3,
故选:C.
2.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
3.解:∵直线l1∥l2∥l3,
∴,
∵,DF=DE+EF.
∴,
故选:D.
4.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
5.解:∵DE∥AB,
∴,
故选:D.
6.解:∵l1∥l2∥l3,
∴,,,,
故选:D.
7.解:∵EF∥BC,
∴=,=,==,
∴选项A,C,D正确,
故选:B.
8.解:∵DE∥BC,DH∥AC,
∴四边形DECH是平行四边形,
∴DH=CE,DE=CH,
∵DE∥BC,
∴==,故选项A正确,不符合题意,
∵DH∥CG,
∴==,故C正确,不符合题意,
∵DE∥BC,
∴=,
∴=,故D正确,不符合题意,
故选:B.
9.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
10.解:如图,过点E作EM⊥AB于M,EN⊥BC于N,作ET∥CB交AD于T.
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN,
∴==,
∴=,
∴=,
∵ET∥CD,
∴==,
∵CD=BD,
∴=,
∴==,
∴=,
∴=,
故选:C.
二.填空题(共5小题,满分20分)
11.解:∵l1∥l2∥l1,
∴=,
∴=,
∴BC=,
∴AC=AB+BC=1+=,
故答案为:.
12.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
13.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
14.解:∵EF∥CD,AE=2EC,
∴==2,
∵DE∥BC,
∴==2,
设DF=m,则AF=2m,AD=3m,DB=m,
∴AF:DF:DB=2m:m:m=4:2:3.
故答案为:4:2:3.
15.解:∵l1∥l2∥l3,,
∴==,
∵DF=10,
∴=,
解得:DE=6,
故答案为:6.
三.解答题(共8小题,满分60分)
16.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
17.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
18.解:∵DE∥AC,DF∥BC,
∴四边形DFCE是平行四边形,
∴DE=FC,DF=EC
∵DF∥BC,
∴△ADF∽△ABC,
∴===,
∵AC=8,BC=12,
∴AF=2,DF=3
∴FC=AC﹣AF=8﹣2=6,
∴DE=FC=6,DF=EC=3
∴四边形DECF的周长是DF+CF+CE+DE=3+6+3+6=18.
答:四边形DECF的周长是18.
19.解:
∵=,
∴=,
∵DE∥AC,
∴,
∴.
20.解:∵AB∥CH∥CD,
∴△CGH∽△ABC,△BGH∽△BCD,
∴,,
∴+=+=1,
∵AB=2,CD=3,
∴=1,
∴GH=.
21.解:(1)∵DE∥BC,
∴=,即=,
∴EC=cm;
(2)∵DE∥BC,
∴=,即=,
∴AE=cm,
∴EC=AC﹣AE=4﹣=(cm);
(3)∵DE∥BC,
∴==,
∴DB=AD,
∵DB﹣AD=3cm,
∴AD﹣AD=3cm,解得AD=6cm,
∴DB=×6=9cm.
22.解:∵a∥b∥c,
∴,
即,
解得:EF=.
23.解:∵a∥b∥c,
∴,
∴,
∴DE=,
∵a∥b∥c,
∴,
∴,
∴DO=.
同课章节目录
