4.5相似三角形的性质及其应用 达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.5相似三角形的性质及其应用 达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 10:31:11 | ||
图片预览


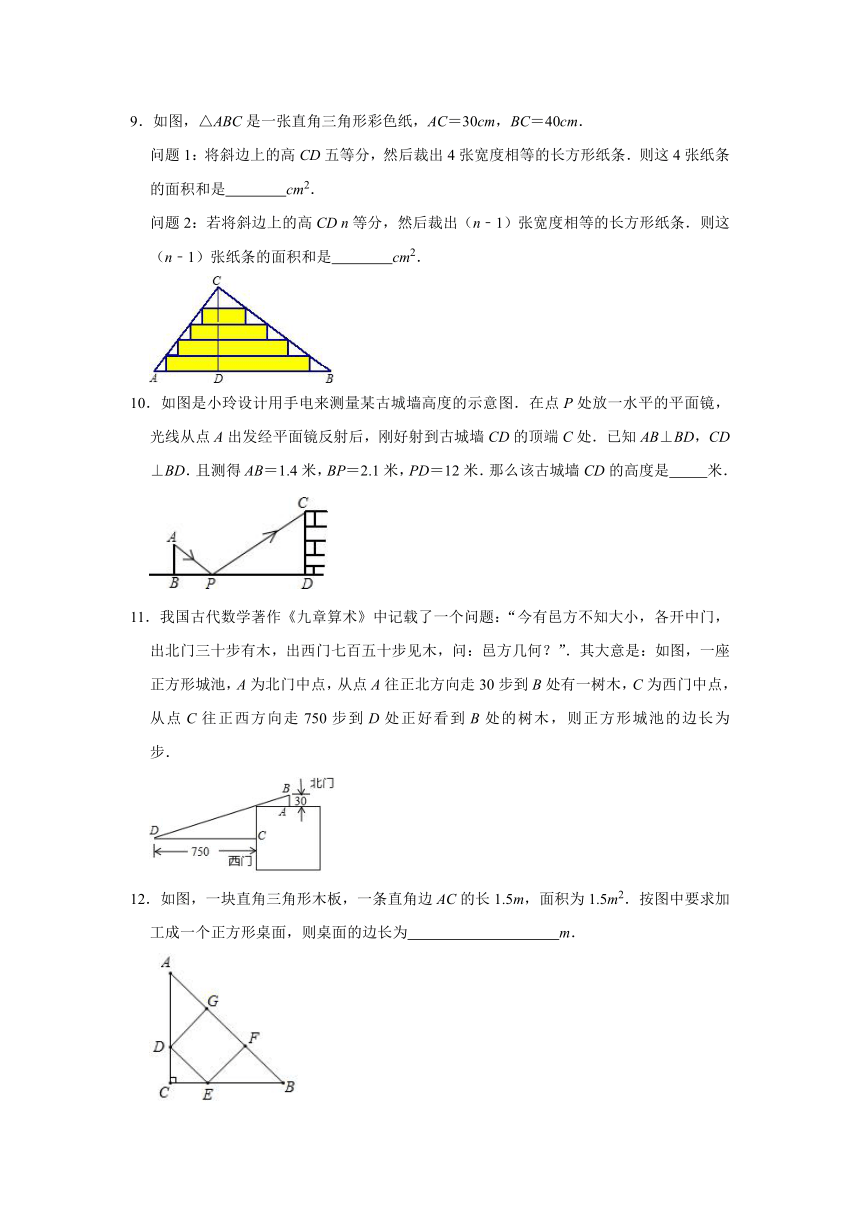

文档简介
2021-2022年浙教版九年级数学上册《4.5相似三角形的性质及其应用》达标测评(附答案)
一.选择题(共7小题,满分28分)
1.如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )
A.6.4米 B.8米 C.9.6米 D.11.2米
2.1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米,此时,若某电视塔的影长为100米,则此电视塔的高度应是( )
A.80米 B.85米 C.120米 D.125米
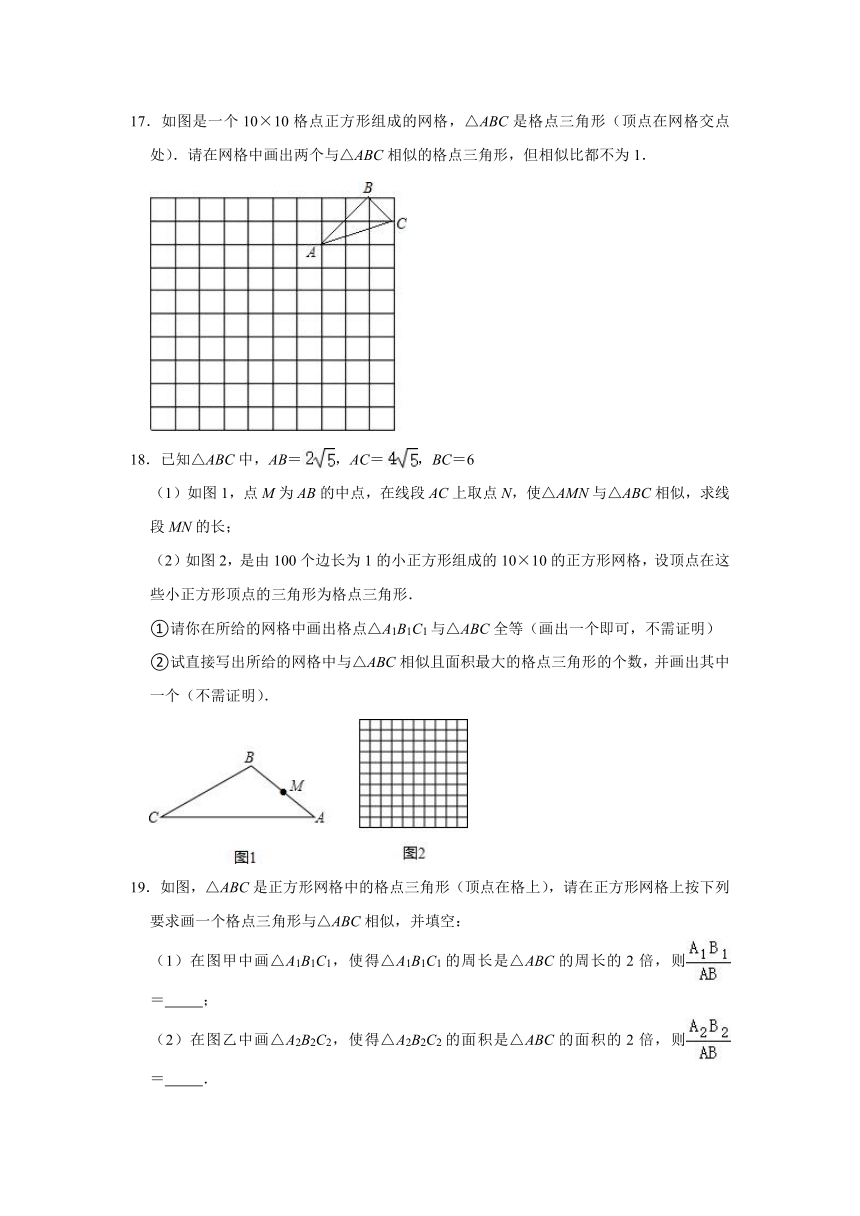
3.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条.如图,在Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm的矩形纸条a1,a2,…,an.若使裁得的矩形纸条的长不小于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数为( )
A.24 B.25 C.26 D.27
4.为测量被池塘相隔的两棵树A,B的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:(1)AC,∠ACB(2)CD,∠ACB,∠ADB(3)EF,DE,AD,其中能根据所测数据求得A,B两树距离的有( )
A.0组 B.一组 C.二组 D.三组
5.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )
A.20m B.m C.10m D.30m
6.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( )
A.11.5米 B.11.75米 C.11.8米 D.12.25米
7.如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
A.3米 B.4米 C.4.5米 D.6米
二.填空题(共8小题,满分32分)
8.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为 米.
9.如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.
问题1:将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.则这4张纸条的面积和是 cm2.
问题2:若将斜边上的高CD n等分,然后裁出(n﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是 cm2.
10.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 米.
11.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
12.如图,一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2.按图中要求加工成一个正方形桌面,则桌面的边长为 m.
13.如图,跷跷板AB长为5米,O为支点,当AO=3米时,坐在A端的人可以将B端的人跷高1米.那么当支点O在AB的中点时,A端的人下降同样的高度可以将B端的人跷高 米.
14.小华在距离路灯6米的地方,发现自己在地面上的影长是2米,如果小华的身高为1.6米,那么路灯离地面的高度是 米.
15.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为 米.
三.解答题(共9小题,满分60分)
16.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
17.如图是一个10×10格点正方形组成的网格,△ABC是格点三角形(顶点在网格交点处).请在网格中画出两个与△ABC相似的格点三角形,但相似比都不为1.
18.已知△ABC中,AB=,AC=,BC=6
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明)
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
19.如图,△ABC是正方形网格中的格点三角形(顶点在格上),请在正方形网格上按下列要求画一个格点三角形与△ABC相似,并填空:
(1)在图甲中画△A1B1C1,使得△A1B1C1的周长是△ABC的周长的2倍,则= ;
(2)在图乙中画△A2B2C2,使得△A2B2C2的面积是△ABC的面积的2倍,则= .
20.正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).
21.如图,已知△ABC.只用直尺(没有刻度的尺)和圆规,求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(要求保留作图痕迹,不必写出作法)
22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.
(1)所需的测量工具是: ;
(2)请在图中画出测量示意图;
(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.
24.如图,为了测量一栋大楼的高度,李青同学在她的脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.如果李青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,问这栋大楼有多高?
参考答案
一.选择题(共7小题,满分28分)
1.解:根据题意,设路灯高度为x米,则=,
解得x=9.6
故选:C.
2.解:设电视塔的高度应是x,根据题意得:,
解得:x=125米.
故选:D.
3.解:设所求的矩形有x张,其中最小的矩形的长为ycm,
则
∴y=40﹣,
又∵y≥5,
∴40﹣≥5,
∴x≤26,
∴最多能裁26张.
故选:C.
4.解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中因为△ABD∽△EFD可利用=,求出AB.
故选:D.
5.解:∵AB⊥DE,BC⊥AB,
∴△ADE∽△ABC,
∴=,
即=,
解得AD=20.
故选:A.
6.解:设树在第一级台阶上面的部分高x米,
则,
解得x=11.5,
∴树高是11.5+0.3=11.8米.
故选:C.
7.解:如图,由题意得,△ACD∽△ABE,
∴=,
即=,
解得BE=6,
即树的高度为6米.
故选:D.
二.填空题(共8小题,满分32分)
8.解:∵BC⊥AD,DE⊥AD,
∴BC∥DE,
∴△ABC∽△ADE,
=,
解得h=,
故答案为.
9.解:问题1:∵△ABC是直角三角形,AC=30cm,BC=40cm.
∴AB==50,
∴AC BC=AB CD,
∴AC BC=AB CD,
∴30×40=50 CD,
∴CD=24cm.
于是知纸条宽度为=4.8cm.
∵=,
又∵AB=50cm,
∴EF=10cm,
同理,GH=20cm,
IJ=30cm,
KL=40cm.
于是4张纸条的面积和为(10+20+30+40)×4.8=480cm2.
问题2:由(1)中规律,(n﹣1)张纸条的面积和为:
cm2.
10.解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=即=
解得:CD=8米.
11.解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
12.解:∵一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2,
∴另一直角边长为:=2(m),
则斜边长为:=2.5,
设点C到AB的距离为h,
则S△ABC=×2.5h=1.5,
解得:h=1.2,
∵正方形GFDE的边DE∥GF,
∴△ACB∽△DCE,
=,
即=,
解得:x=,
故答案为:.
13.解:如图,DF表示A端下降的高度,GE表示B端上升的高度,
依题意知道,△DOF∽△EOG,
∴DF:EG=OD:OE,
∵OA=OD=3,OB=OE=2,EG=1,
∴DF:1=3:2,
∴DF=1.5,
当O在AB中点的时候,
OA=OD=OB=OE,
∴△DOF≌△EOG,
∴DF=EG=1.5.
故答案为:1.5.
14.解:根据题意画出图形,易得△ADE∽△ABC,
根据相似三角形的性质,
得=,
即=,解得h=6.4m.
15.解:方法1、如图,设从墙上的影子的顶端到树的顶端的垂直高度是x米.
则有,解得x=3.
∴树高是3+1.2=4.2(米),
故答案为4.2.
方法2、将落在墙上的影子看作物体,此时它的影子设为a米,
根据题意得,,
∴a=0.96,
所以大树的影子全部落在地面上的影子长为2.4+0.96=3.36米,
设树的高度为y米,根据题意得,,
∴y=4.2米
故答案为:4.2.
三.解答题(共9小题,满分60分)
16.解:(1)不存在.
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,
所以不存在;
(2)不存在.
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
17.解:
18.解:(1)①∵△AMN∽△ABC,
∴=
∵M为AB中点,AB=2,
∴AM=,
∵BC=6,
∴MN=3;
②∵△AMN∽△ACB,
∴=,
∵BC=6,AC=4,AM=,
∴MN=1.5;
(2)①如图所示:
②每条对角线处可作4个三角形与原三角形相似,那么共有8个.
19.解:(1)2;
(2)(每个填空题正确得(1分),每个图形画正确得2分)
20.解:根据题意画出图形,如图所示:
21.解:画图
△DEF就是所求三角形(5分),结论(1分).
22.解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP.
∴,
即,
解得,MA=5米;
同理,由△NBD∽△NOP,可求得NB=1.5米,
∴小明的身影变短了5﹣1.5=3.5米.
23.解:(1)皮尺,标杆;
(2)测量示意图如图所示;
(3)如图,测得标杆DE=a,树和标杆的影长分别为AC=b,EF=c,
∵△DEF∽△BAC,
∴,
∴,
∴.
24.解:根据题意,
∵∠KLM=∠TSM=90°,∠KML=∠TMS(反射角等于入射角),
∴△KLM∽△TSM,
∴,即(4分)
∴TS=125(m)(3分)
所以这栋大楼高为125m.(1分)
一.选择题(共7小题,满分28分)
1.如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )
A.6.4米 B.8米 C.9.6米 D.11.2米
2.1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米,此时,若某电视塔的影长为100米,则此电视塔的高度应是( )
A.80米 B.85米 C.120米 D.125米
3.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条.如图,在Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm的矩形纸条a1,a2,…,an.若使裁得的矩形纸条的长不小于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数为( )
A.24 B.25 C.26 D.27
4.为测量被池塘相隔的两棵树A,B的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:(1)AC,∠ACB(2)CD,∠ACB,∠ADB(3)EF,DE,AD,其中能根据所测数据求得A,B两树距离的有( )
A.0组 B.一组 C.二组 D.三组
5.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )
A.20m B.m C.10m D.30m
6.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( )
A.11.5米 B.11.75米 C.11.8米 D.12.25米
7.如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
A.3米 B.4米 C.4.5米 D.6米
二.填空题(共8小题,满分32分)
8.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为 米.
9.如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.
问题1:将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.则这4张纸条的面积和是 cm2.
问题2:若将斜边上的高CD n等分,然后裁出(n﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是 cm2.
10.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 米.
11.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
12.如图,一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2.按图中要求加工成一个正方形桌面,则桌面的边长为 m.
13.如图,跷跷板AB长为5米,O为支点,当AO=3米时,坐在A端的人可以将B端的人跷高1米.那么当支点O在AB的中点时,A端的人下降同样的高度可以将B端的人跷高 米.
14.小华在距离路灯6米的地方,发现自己在地面上的影长是2米,如果小华的身高为1.6米,那么路灯离地面的高度是 米.
15.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为 米.
三.解答题(共9小题,满分60分)
16.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
17.如图是一个10×10格点正方形组成的网格,△ABC是格点三角形(顶点在网格交点处).请在网格中画出两个与△ABC相似的格点三角形,但相似比都不为1.
18.已知△ABC中,AB=,AC=,BC=6
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明)
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
19.如图,△ABC是正方形网格中的格点三角形(顶点在格上),请在正方形网格上按下列要求画一个格点三角形与△ABC相似,并填空:
(1)在图甲中画△A1B1C1,使得△A1B1C1的周长是△ABC的周长的2倍,则= ;
(2)在图乙中画△A2B2C2,使得△A2B2C2的面积是△ABC的面积的2倍,则= .
20.正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).
21.如图,已知△ABC.只用直尺(没有刻度的尺)和圆规,求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(要求保留作图痕迹,不必写出作法)
22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.
(1)所需的测量工具是: ;
(2)请在图中画出测量示意图;
(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.
24.如图,为了测量一栋大楼的高度,李青同学在她的脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.如果李青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,问这栋大楼有多高?
参考答案
一.选择题(共7小题,满分28分)
1.解:根据题意,设路灯高度为x米,则=,
解得x=9.6
故选:C.
2.解:设电视塔的高度应是x,根据题意得:,
解得:x=125米.
故选:D.
3.解:设所求的矩形有x张,其中最小的矩形的长为ycm,
则
∴y=40﹣,
又∵y≥5,
∴40﹣≥5,
∴x≤26,
∴最多能裁26张.
故选:C.
4.解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中因为△ABD∽△EFD可利用=,求出AB.
故选:D.
5.解:∵AB⊥DE,BC⊥AB,
∴△ADE∽△ABC,
∴=,
即=,
解得AD=20.
故选:A.
6.解:设树在第一级台阶上面的部分高x米,
则,
解得x=11.5,
∴树高是11.5+0.3=11.8米.
故选:C.
7.解:如图,由题意得,△ACD∽△ABE,
∴=,
即=,
解得BE=6,
即树的高度为6米.
故选:D.
二.填空题(共8小题,满分32分)
8.解:∵BC⊥AD,DE⊥AD,
∴BC∥DE,
∴△ABC∽△ADE,
=,
解得h=,
故答案为.
9.解:问题1:∵△ABC是直角三角形,AC=30cm,BC=40cm.
∴AB==50,
∴AC BC=AB CD,
∴AC BC=AB CD,
∴30×40=50 CD,
∴CD=24cm.
于是知纸条宽度为=4.8cm.
∵=,
又∵AB=50cm,
∴EF=10cm,
同理,GH=20cm,
IJ=30cm,
KL=40cm.
于是4张纸条的面积和为(10+20+30+40)×4.8=480cm2.
问题2:由(1)中规律,(n﹣1)张纸条的面积和为:
cm2.
10.解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=即=
解得:CD=8米.
11.解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
12.解:∵一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2,
∴另一直角边长为:=2(m),
则斜边长为:=2.5,
设点C到AB的距离为h,
则S△ABC=×2.5h=1.5,
解得:h=1.2,
∵正方形GFDE的边DE∥GF,
∴△ACB∽△DCE,
=,
即=,
解得:x=,
故答案为:.
13.解:如图,DF表示A端下降的高度,GE表示B端上升的高度,
依题意知道,△DOF∽△EOG,
∴DF:EG=OD:OE,
∵OA=OD=3,OB=OE=2,EG=1,
∴DF:1=3:2,
∴DF=1.5,
当O在AB中点的时候,
OA=OD=OB=OE,
∴△DOF≌△EOG,
∴DF=EG=1.5.
故答案为:1.5.
14.解:根据题意画出图形,易得△ADE∽△ABC,
根据相似三角形的性质,
得=,
即=,解得h=6.4m.
15.解:方法1、如图,设从墙上的影子的顶端到树的顶端的垂直高度是x米.
则有,解得x=3.
∴树高是3+1.2=4.2(米),
故答案为4.2.
方法2、将落在墙上的影子看作物体,此时它的影子设为a米,
根据题意得,,
∴a=0.96,
所以大树的影子全部落在地面上的影子长为2.4+0.96=3.36米,
设树的高度为y米,根据题意得,,
∴y=4.2米
故答案为:4.2.
三.解答题(共9小题,满分60分)
16.解:(1)不存在.
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,
所以不存在;
(2)不存在.
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
17.解:
18.解:(1)①∵△AMN∽△ABC,
∴=
∵M为AB中点,AB=2,
∴AM=,
∵BC=6,
∴MN=3;
②∵△AMN∽△ACB,
∴=,
∵BC=6,AC=4,AM=,
∴MN=1.5;
(2)①如图所示:
②每条对角线处可作4个三角形与原三角形相似,那么共有8个.
19.解:(1)2;
(2)(每个填空题正确得(1分),每个图形画正确得2分)
20.解:根据题意画出图形,如图所示:
21.解:画图
△DEF就是所求三角形(5分),结论(1分).
22.解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP.
∴,
即,
解得,MA=5米;
同理,由△NBD∽△NOP,可求得NB=1.5米,
∴小明的身影变短了5﹣1.5=3.5米.
23.解:(1)皮尺,标杆;
(2)测量示意图如图所示;
(3)如图,测得标杆DE=a,树和标杆的影长分别为AC=b,EF=c,
∵△DEF∽△BAC,
∴,
∴,
∴.
24.解:根据题意,
∵∠KLM=∠TSM=90°,∠KML=∠TMS(反射角等于入射角),
∴△KLM∽△TSM,
∴,即(4分)
∴TS=125(m)(3分)
所以这栋大楼高为125m.(1分)
同课章节目录
