2.1有理数加法1

(共23张PPT)
福州
金华
广州
上升1 ℃
上升2 ℃
（+1）+（+2）=+3
金华
广州
北京
上升3℃
（+3）+（ － 1 0）=？
下降10 ℃
上升 － 1 0℃
1. 一间0℃的冷藏室连续两次改变温度：
第一次下降5℃，接着再下降15℃.
问：两次变化使温度共上升了多少摄氏度
上升了－20℃
-25
-20
-15
-10
-5
0
5
10
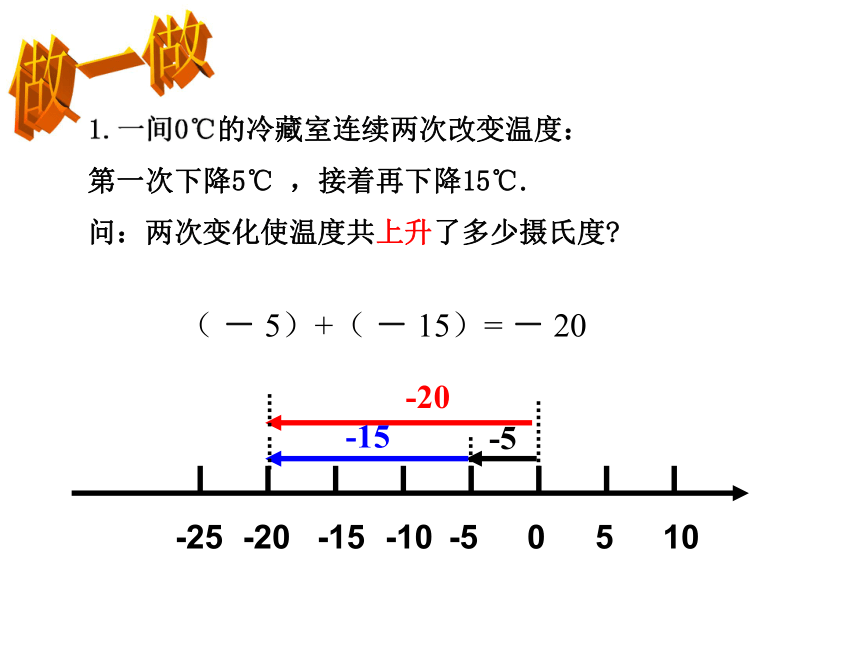
1.一间0℃的冷藏室连续两次改变温度：
第一次下降5℃ ，接着再下降15℃.
问：两次变化使温度共上升了多少摄氏度
（ － 5）+（ － 15）= － 20
-5
-15
-20
2.一间0℃的冷藏室连续两次改变温度：
第一次下降15℃ ，接着再上升10℃.
问：两次变化使温度共上升了多少摄氏度
上升了－ 5 ℃
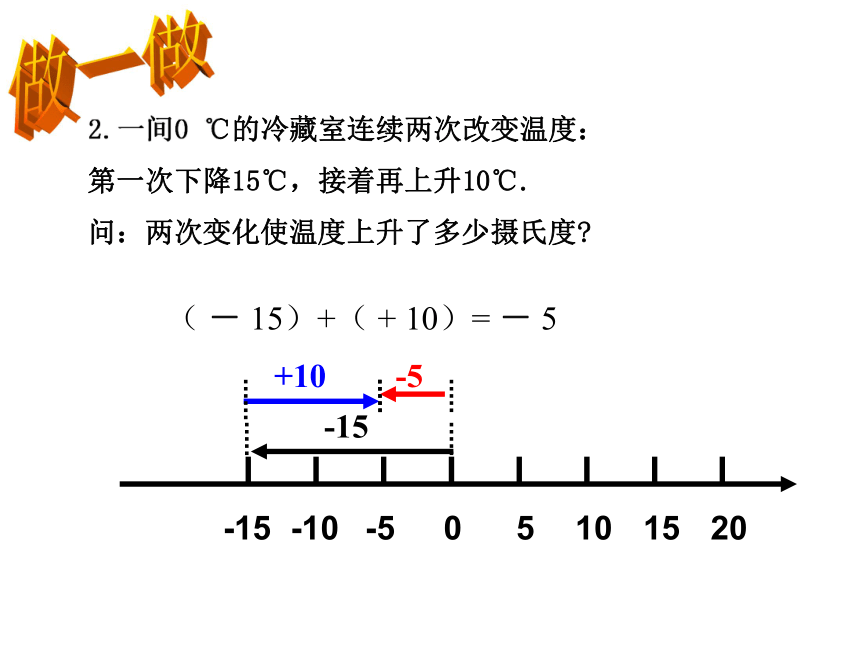
2.一间0 ℃的冷藏室连续两次改变温度：
第一次下降15℃，接着再上升10℃.
问：两次变化使温度上升了多少摄氏度
（ － 15）+（ + 10）= － 5
-15
+10
-5
-15
-10
-5
0
5
10
15
20
3.一间0℃的冷藏室连续两次改变温度：
第一次上升15℃，接着再下降了10℃.
问：两次变化使温度共上升了多少摄氏度
上升了+ 5 ℃
3.一间0℃的冷藏室连续两次改变温度：
第一次上升15℃ ，接着再下降了10℃.
问：两次变化使温度上升了多少摄氏度
（ + 15）+（ － 10）= +5
+15
-10
+5
-15
-10
-5
0
5
10
15
20
(1)（+1）+（+2）=+3
(2)（- 5）+（-15）= -20
(3)（- 15）+（+10）= -5
(4)（ +15）+（-10）=+5
请你联系生活实际算一算，并把自己的算法说一说
(1)（+ 5）+（-5）= ？
(2)（- 5）+ 0 = ？
(3)（ +5）+ 0 =？
0
-5
+5
(1)（+1）+（+2）=+3
(2)（- 5）+（-15）= -20
(3)（- 15）+（+10）= -5
(4)（+15）+（-10）=+5
(5)（+5）+（-5）= 0
(6)（- 5）+ 0 = -5
(7)（+5）+ 0 = +5
你能把下列7个式子进行分类吗？说出你分类的理由。
（+1）+（+2）=+3
（- 5）+（-15）= -20
（- 15）+（+10）= -5
（ +15）+（-10）=+5
（ +5）+（-5）= 0
（- 5）+ 0 = -5
（+5）+ 0 = +5
同号两数相加
异号两数相加
一个数与零相加
你能按照上面的分类试着总结有理数加法的运算法则吗？
总结的过程中，请注意以下两个问题：
（1）和的符号有什么决定？
（2）两个加数的绝对值与和的绝对值有什么关系？
●同号两数相加，取与加数相同的符号，并把绝对值相加.
●异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.
●一个数同0相加，仍得这个数.
●互为相反数的两个数相加得0.
计算：
(- 35)+(-17) (2) (-3.5)+ (+12.5)
(3) 11+(-13) (4) 1.07 +(-1.07)
活动1：请同学们拿出有理数牌，同组间进行有理数加法运算比赛.比赛规则：不仅要算得快，还要说明算法.
活动2：请获胜的学生谈谈获胜的秘诀。
9,11.ppt
在括号里填上适当的数，使下列式子成立：
1、( -10 )+( )= 0 　　　 2、( )+( -21 )= -8
3、( -20 )+( )= -31
4、a+( )=0
+10
+13
-11
-a
9,11.ppt
两个数的和为负,则这两个数( )
　A. 一个为正数，一个为负数　　
　B. 同为负数
　C. 一个为零，一个为负数
　D. 至少一个为负数
D
9,11.ppt
1.一个数是2的相反数，另一个数的绝对值是5，求这两个数的和.
2.两个数的和一定大于每个加数吗？
课堂作业：
作业本