2021-2022学年浙教版九年级数学上册4.5相似三角形的性质及其应用 同步训练 (word版、含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册4.5相似三角形的性质及其应用 同步训练 (word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 361.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 16:45:47 | ||
图片预览



文档简介
2021-2022学年浙教版九年级数学上册《4.5相似三角形的性质及其应用》
同步训练(附答案)
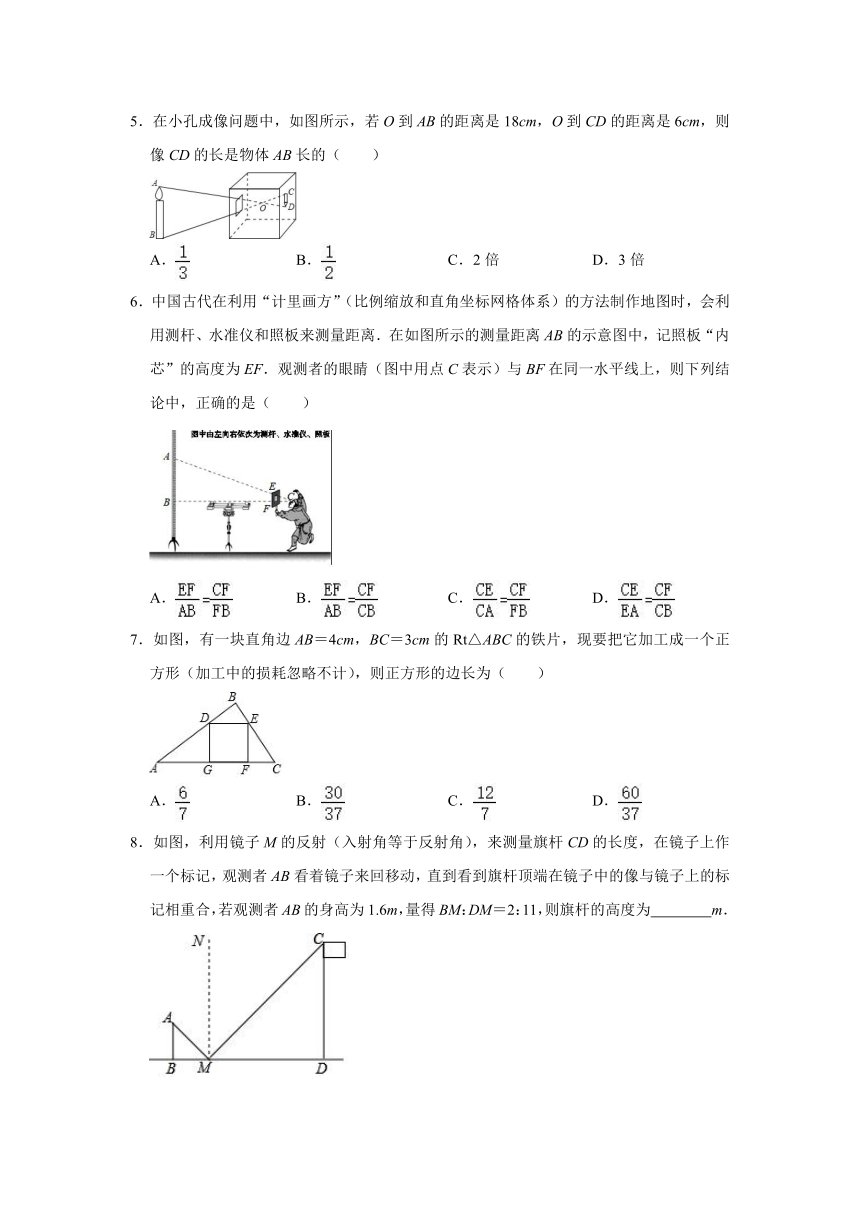
1.如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是( )
A.5m B.6m C.125m D.4m
2.如图,夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )
A.8m B.6.4m C.4.8m D.10m
3.一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为正方形的纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
4.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB是( )
A.4米 B.4.5米 C.5米 D.5.5米
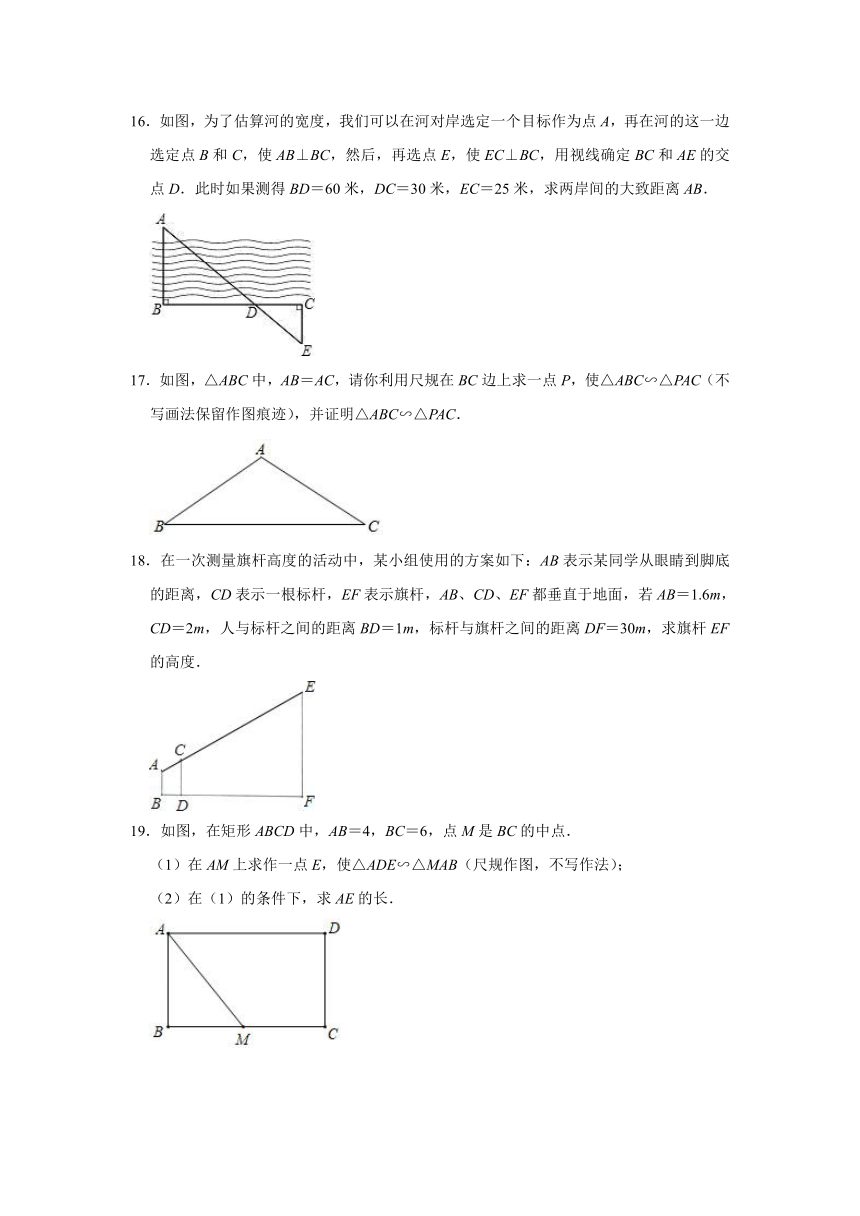
5.在小孔成像问题中,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A. B. C.2倍 D.3倍
6.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
7.如图,有一块直角边AB=4cm,BC=3cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
8.如图,利用镜子M的反射(入射角等于反射角),来测量旗杆CD的长度,在镜子上作一个标记,观测者AB看着镜子来回移动,直到看到旗杆顶端在镜子中的像与镜子上的标记相重合,若观测者AB的身高为1.6m,量得BM:DM=2:11,则旗杆的高度为 m.
9.如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=120cm,CD=600cm,则树AB的高度为 cm.
10.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2米,CD=5米,点P到CD的距离是3米,则P到AB的距离是 米.
11.太原市某学校门口的栏杆如图所示,栏杆从水平位置AB绕定点O旋转到DC位置,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m.支柱OE的高为0.5m,则栏杆D端离地面的距离为 .
12.“今有井径五尺,不知其深,立五尺于井上,从木末望水岸,入径2尺,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,请你求出井深BD.
13.如图,小明欲测量一座古塔的高度,他拿出一根竹竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹竿顶端离地面2.4m,小明到竹竿的距离DF=2m,竹竿到塔底的距离DB=32m,求这座古塔的高度.
14.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
15.“福龙丽景”的居民筹集资金650元,计划在楼前一块上底5m、下底10m的梯形(如图①)空地上种植花草,美化环境.
(1)试求△AED与△BEC的面积比;
(2)他们在△AED和△BEC地带上种康乃馨,单价为10元/m2,共花250元.若其余地带(△ABE和△DCE)可种兰花或茉莉花,单价分别为20元/m2、15元/m2,那么应选择种哪种花,刚好用完所筹集资金?
(3)若梯形ABCD为等腰梯形(如图②),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC,S△APD=S△BPC,并说明理由.
16.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=60米,DC=30米,EC=25米,求两岸间的大致距离AB.
17.如图,△ABC中,AB=AC,请你利用尺规在BC边上求一点P,使△ABC∽△PAC(不写画法保留作图痕迹),并证明△ABC∽△PAC.
18.在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.
19.如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
20.小明用这样的方法来测量建筑物的高度:如图所示,在地面上(E处)放一面镜子,他刚好从镜子中看到建筑物(AB)的顶端B,他的眼睛离地面1.25米(CD=1.25米),如果小明离镜子1.50米(CE=1.50米),与建筑物的距离是181.50米(CA=181.50米).那么建筑物的高是多少米?
21.为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
参考答案
1.解:作AN⊥EF于N,交BC于M,
∵BC∥EF,
∴AM⊥BC于M,
∴△ABC∽△AEF,
∴=,
∵AM=0.7m,AN=25m,BC=0.14m,
∴EF===5(m).
故选:A.
2.解:如图,∵BC=3.2m,CA=0.8m,
∴AB=AC+BC=0.8+3.2=4cm,
∵小玲与大树都与地面垂直,
∴△ACE∽△ABD,
∴=,
即=,
解得BD=8.
故选:A.
3.解:如图,BC=15,AF=22.5,DE=3,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
∴AH=4.5,
∴HF=22.5﹣4.5=18,
而18÷3=6,
∴裁得的纸条中恰为正方形的纸条是第6张.
故选:C.
4.解:在△DEF和△DBC中,,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4,
∵AC=1.5m,
∴AB=AC+BC=1.5+4=5.5m,
即树高5.5m.
故选:D.
5.解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
6.解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:B.
7.解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC= AB BC= AC BP,
∴BP===.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴=.
设DE=x,则有:=,
解得x=,
故选:D.
8.解:根据题意得:△ABM∽△CDM,
∴AB:CD=BM:DM,
∵AB=1.6m,BM:DM=2:11,
∴1.6:CD=2:11,
解得:CD=8.8m,
故答案为:8.8.
9.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm,EF=15cm,AC=120cm,CD=600cm,
∴,
∴BC=300cm,
∴AB=AC+BC=120+300=420cm,
故答案为:420.
10.解:∵AB∥CD
∴△PAB∽△PCD
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:5=P到AB的距离:3
∴P到AB的距离为m,
故答案为.
11.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.5m,
∴栏杆D端离地面的距离为1.8+0.5=2.3m.
故答案是:2.3m.
12.解:依题意可得:△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=2:5,
解得:AD=12.5,
BD=AD﹣AB=12.5﹣5=7.5尺.
所以井深BD为7.5尺.
13.解:∵小明、竹竿、古塔均与地面垂直,EH⊥AB,
∴BH=DG=EF=1.5m,EG=DF,GH=DB,
∵小明眼睛离地面1.5m,竹竿顶端离地面2.4m,
∴CG=CD﹣EF=2.4﹣1.5=0.9m,
∵CD∥AB,
∴△EGC∽△EHA
∵DF=2mDB=32m,
∴,
即=,
解得:AH=15.3m,
∴AB=AH+BH=15.3+1.5=16.8m,
答:古塔的高度是16.8m.
14.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
15.解:(1)∵梯形ABCD的边AD∥BC,
∴△AED∽△BEC,
∴△AED与△BEC的面积比=(AD:BC)2=(5:10)2=1:4;
(2)设△AED的边AD上的高为h,
∵△AED∽△BEC,
∴△BEC的边BC上的高为h=2h,
∴×5h+×10×2h=250÷10,
解得h=2,
∴梯形的高为h+2h=2+2×2=6,
△ABE和△DCE的面积之和=×(5+10)×6﹣250÷10=45﹣25=20m2,
∴所种花的单价=(650﹣250)÷20=20元/m2,
答:选择种兰花,刚好用完所筹集资金;
(3)∵△APB≌△DPC,
∴点P在对称轴上,
∵AD=5cm,BC=10cm,S△APD=S△BPC,
∴点P到AD的距离等于到BC的距离的2倍,
点P的位置如图所示.
16.解:∵∠ADB=∠CDE,∠ABD=∠ECD=90°,
∴△BAD∽△CED,
∴=,
即=,
∴AB=50.
答:两岸间的大致距离AB为50米.
17.解:如图所示:点P即为所求,
∵MN是AC的垂直平分线,交BC于点P,
∴AP=CP,
∴∠C=∠PAC,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C=∠PAC,
∴△ABC∽△PAC.
18.解:过点A作AH⊥EF于H点,AH交CD于G,
∵CD∥EF,
∴△ACG∽△AEH,
∴,
即:,
∴EH=12.4.
∴EF=EH+HF=12.4+1.6=14,
∴旗杆的高度为14米.
19.解(1)过D 作DE⊥AM于E,△ADE即为所求;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=,
∴AE===.
20.解:∵AC=181.5、CE=1.5,
∴AE=180,
根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴=,即=,
解得AB=150.
答:建筑物的高是150米.
21.解:如图所示:过点E作EB⊥AC于点B,
由题意可得:DC=BE=4.6m,DE=BC=2.5m,
∵同一时刻身高1.5米小刚站立时在太阳光下的影长恰好为1米,
∴==,
解得:AB=6.9,
故AC=AB+BC=6.9+2.5=9.4(m),
答:新安装的照明路灯的灯杆的高度为9.4m.
同步训练(附答案)
1.如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是( )
A.5m B.6m C.125m D.4m
2.如图,夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )
A.8m B.6.4m C.4.8m D.10m
3.一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为正方形的纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
4.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB是( )
A.4米 B.4.5米 C.5米 D.5.5米
5.在小孔成像问题中,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A. B. C.2倍 D.3倍
6.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
7.如图,有一块直角边AB=4cm,BC=3cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
8.如图,利用镜子M的反射(入射角等于反射角),来测量旗杆CD的长度,在镜子上作一个标记,观测者AB看着镜子来回移动,直到看到旗杆顶端在镜子中的像与镜子上的标记相重合,若观测者AB的身高为1.6m,量得BM:DM=2:11,则旗杆的高度为 m.
9.如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=120cm,CD=600cm,则树AB的高度为 cm.
10.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2米,CD=5米,点P到CD的距离是3米,则P到AB的距离是 米.
11.太原市某学校门口的栏杆如图所示,栏杆从水平位置AB绕定点O旋转到DC位置,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m.支柱OE的高为0.5m,则栏杆D端离地面的距离为 .
12.“今有井径五尺,不知其深,立五尺于井上,从木末望水岸,入径2尺,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,请你求出井深BD.
13.如图,小明欲测量一座古塔的高度,他拿出一根竹竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹竿顶端离地面2.4m,小明到竹竿的距离DF=2m,竹竿到塔底的距离DB=32m,求这座古塔的高度.
14.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
15.“福龙丽景”的居民筹集资金650元,计划在楼前一块上底5m、下底10m的梯形(如图①)空地上种植花草,美化环境.
(1)试求△AED与△BEC的面积比;
(2)他们在△AED和△BEC地带上种康乃馨,单价为10元/m2,共花250元.若其余地带(△ABE和△DCE)可种兰花或茉莉花,单价分别为20元/m2、15元/m2,那么应选择种哪种花,刚好用完所筹集资金?
(3)若梯形ABCD为等腰梯形(如图②),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC,S△APD=S△BPC,并说明理由.
16.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=60米,DC=30米,EC=25米,求两岸间的大致距离AB.
17.如图,△ABC中,AB=AC,请你利用尺规在BC边上求一点P,使△ABC∽△PAC(不写画法保留作图痕迹),并证明△ABC∽△PAC.
18.在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.
19.如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
20.小明用这样的方法来测量建筑物的高度:如图所示,在地面上(E处)放一面镜子,他刚好从镜子中看到建筑物(AB)的顶端B,他的眼睛离地面1.25米(CD=1.25米),如果小明离镜子1.50米(CE=1.50米),与建筑物的距离是181.50米(CA=181.50米).那么建筑物的高是多少米?
21.为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
参考答案
1.解:作AN⊥EF于N,交BC于M,
∵BC∥EF,
∴AM⊥BC于M,
∴△ABC∽△AEF,
∴=,
∵AM=0.7m,AN=25m,BC=0.14m,
∴EF===5(m).
故选:A.
2.解:如图,∵BC=3.2m,CA=0.8m,
∴AB=AC+BC=0.8+3.2=4cm,
∵小玲与大树都与地面垂直,
∴△ACE∽△ABD,
∴=,
即=,
解得BD=8.
故选:A.
3.解:如图,BC=15,AF=22.5,DE=3,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
∴AH=4.5,
∴HF=22.5﹣4.5=18,
而18÷3=6,
∴裁得的纸条中恰为正方形的纸条是第6张.
故选:C.
4.解:在△DEF和△DBC中,,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4,
∵AC=1.5m,
∴AB=AC+BC=1.5+4=5.5m,
即树高5.5m.
故选:D.
5.解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
6.解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:B.
7.解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC= AB BC= AC BP,
∴BP===.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴=.
设DE=x,则有:=,
解得x=,
故选:D.
8.解:根据题意得:△ABM∽△CDM,
∴AB:CD=BM:DM,
∵AB=1.6m,BM:DM=2:11,
∴1.6:CD=2:11,
解得:CD=8.8m,
故答案为:8.8.
9.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm,EF=15cm,AC=120cm,CD=600cm,
∴,
∴BC=300cm,
∴AB=AC+BC=120+300=420cm,
故答案为:420.
10.解:∵AB∥CD
∴△PAB∽△PCD
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:5=P到AB的距离:3
∴P到AB的距离为m,
故答案为.
11.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.5m,
∴栏杆D端离地面的距离为1.8+0.5=2.3m.
故答案是:2.3m.
12.解:依题意可得:△ABF∽△ADE,
∴AB:AD=BF:DE,
即5:AD=2:5,
解得:AD=12.5,
BD=AD﹣AB=12.5﹣5=7.5尺.
所以井深BD为7.5尺.
13.解:∵小明、竹竿、古塔均与地面垂直,EH⊥AB,
∴BH=DG=EF=1.5m,EG=DF,GH=DB,
∵小明眼睛离地面1.5m,竹竿顶端离地面2.4m,
∴CG=CD﹣EF=2.4﹣1.5=0.9m,
∵CD∥AB,
∴△EGC∽△EHA
∵DF=2mDB=32m,
∴,
即=,
解得:AH=15.3m,
∴AB=AH+BH=15.3+1.5=16.8m,
答:古塔的高度是16.8m.
14.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
15.解:(1)∵梯形ABCD的边AD∥BC,
∴△AED∽△BEC,
∴△AED与△BEC的面积比=(AD:BC)2=(5:10)2=1:4;
(2)设△AED的边AD上的高为h,
∵△AED∽△BEC,
∴△BEC的边BC上的高为h=2h,
∴×5h+×10×2h=250÷10,
解得h=2,
∴梯形的高为h+2h=2+2×2=6,
△ABE和△DCE的面积之和=×(5+10)×6﹣250÷10=45﹣25=20m2,
∴所种花的单价=(650﹣250)÷20=20元/m2,
答:选择种兰花,刚好用完所筹集资金;
(3)∵△APB≌△DPC,
∴点P在对称轴上,
∵AD=5cm,BC=10cm,S△APD=S△BPC,
∴点P到AD的距离等于到BC的距离的2倍,
点P的位置如图所示.
16.解:∵∠ADB=∠CDE,∠ABD=∠ECD=90°,
∴△BAD∽△CED,
∴=,
即=,
∴AB=50.
答:两岸间的大致距离AB为50米.
17.解:如图所示:点P即为所求,
∵MN是AC的垂直平分线,交BC于点P,
∴AP=CP,
∴∠C=∠PAC,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C=∠PAC,
∴△ABC∽△PAC.
18.解:过点A作AH⊥EF于H点,AH交CD于G,
∵CD∥EF,
∴△ACG∽△AEH,
∴,
即:,
∴EH=12.4.
∴EF=EH+HF=12.4+1.6=14,
∴旗杆的高度为14米.
19.解(1)过D 作DE⊥AM于E,△ADE即为所求;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=,
∴AE===.
20.解:∵AC=181.5、CE=1.5,
∴AE=180,
根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴=,即=,
解得AB=150.
答:建筑物的高是150米.
21.解:如图所示:过点E作EB⊥AC于点B,
由题意可得:DC=BE=4.6m,DE=BC=2.5m,
∵同一时刻身高1.5米小刚站立时在太阳光下的影长恰好为1米,
∴==,
解得:AB=6.9,
故AC=AB+BC=6.9+2.5=9.4(m),
答:新安装的照明路灯的灯杆的高度为9.4m.
同课章节目录
