2021-2022学年浙教版九年级数学上册4.6相似多边形同步达标训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册4.6相似多边形同步达标训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 16:47:00 | ||
图片预览


文档简介
2021-2022学年浙教版九年级数学上册《4.6相似多边形》同步达标训练(附答案)
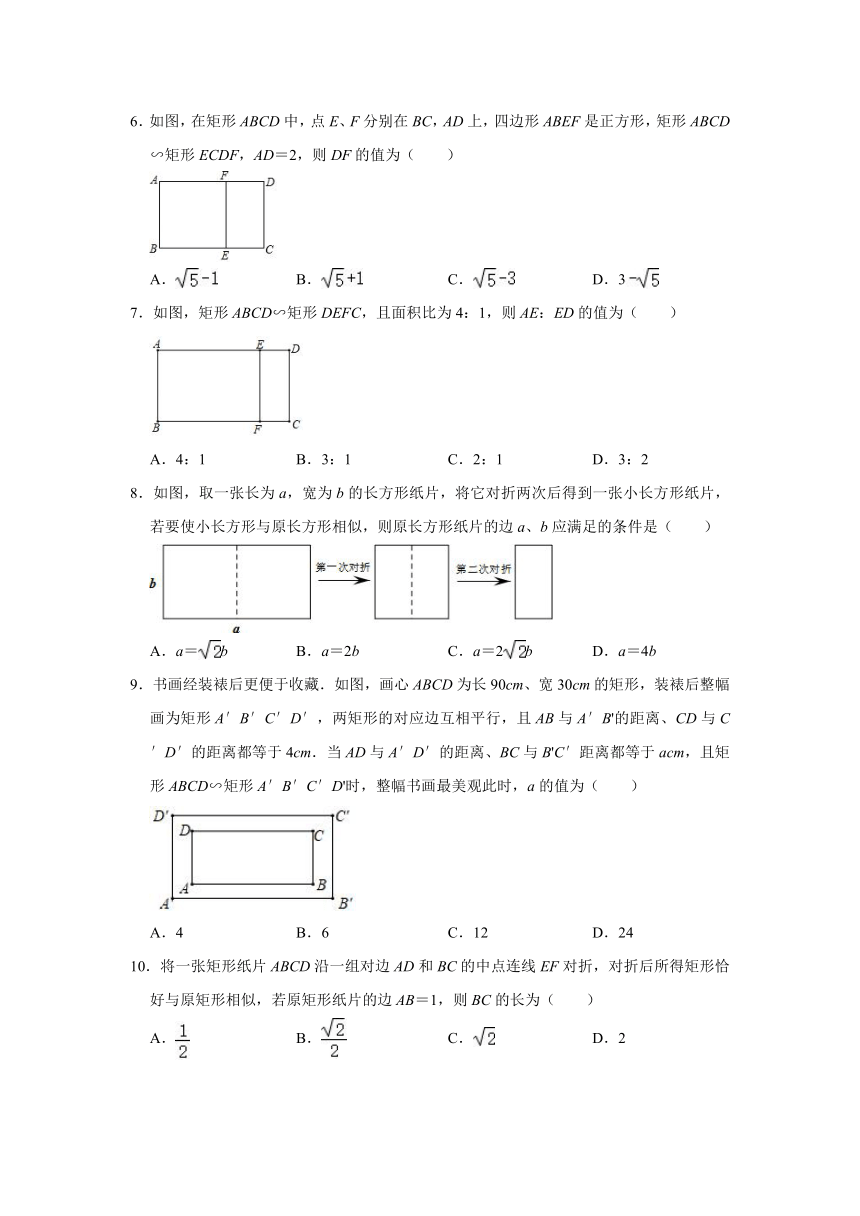
1.下列说法正确的是( )
A.所有菱形都相似 B.所有矩形都相似
C.所有正方形都相似 D.所有平行四边形都相似
2.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( )
A. B. C. D.
3.如图,在矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的点F处,若四边形EFDC(EF>DF)与矩形ABCD相似,则DF的长为( )
A. B. C. D.1
4.矩形的两边长分别为x和6(x<6),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则x的值为( )
A. B. C. D.2.5
5.如图,一张矩形纸片ABCD的长BC=xcm,宽AB=ycm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( )
A. B. C. D.
6.如图,在矩形ABCD中,点E、F分别在BC,AD上,四边形ABEF是正方形,矩形ABCD∽矩形ECDF,AD=2,则DF的值为( )
A. B. C. D.3
7.如图,矩形ABCD∽矩形DEFC,且面积比为4:1,则AE:ED的值为( )
A.4:1 B.3:1 C.2:1 D.3:2
8.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
9.书画经装裱后更便于收藏.如图,画心ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm.当AD与A′D′的距离、BC与B'C′距离都等于acm,且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( )
A.4 B.6 C.12 D.24
10.将一张矩形纸片ABCD沿一组对边AD和BC的中点连线EF对折,对折后所得矩形恰好与原矩形相似,若原矩形纸片的边AB=1,则BC的长为( )
A. B. C. D.2
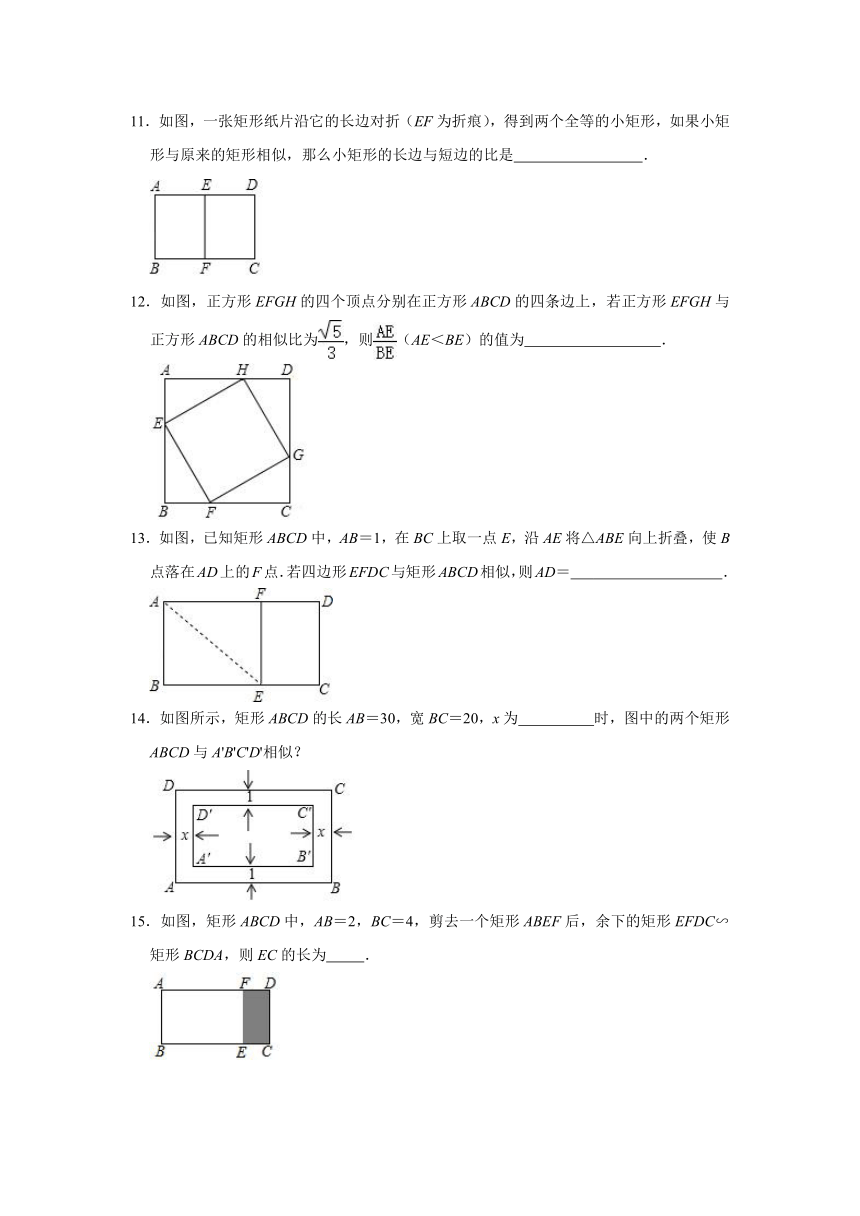
11.如图,一张矩形纸片沿它的长边对折(EF为折痕),得到两个全等的小矩形,如果小矩形与原来的矩形相似,那么小矩形的长边与短边的比是 .
12.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则(AE<BE)的值为 .
13.如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= .
14.如图所示,矩形ABCD的长AB=30,宽BC=20,x为 时,图中的两个矩形ABCD与A'B'C'D'相似?
15.如图,矩形ABCD中,AB=2,BC=4,剪去一个矩形ABEF后,余下的矩形EFDC∽矩形BCDA,则EC的长为 .
16.北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为 丈.
17.如图,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧),且要使四边形DEBF与菱形ABCD相似,则AE的长为 .
18.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
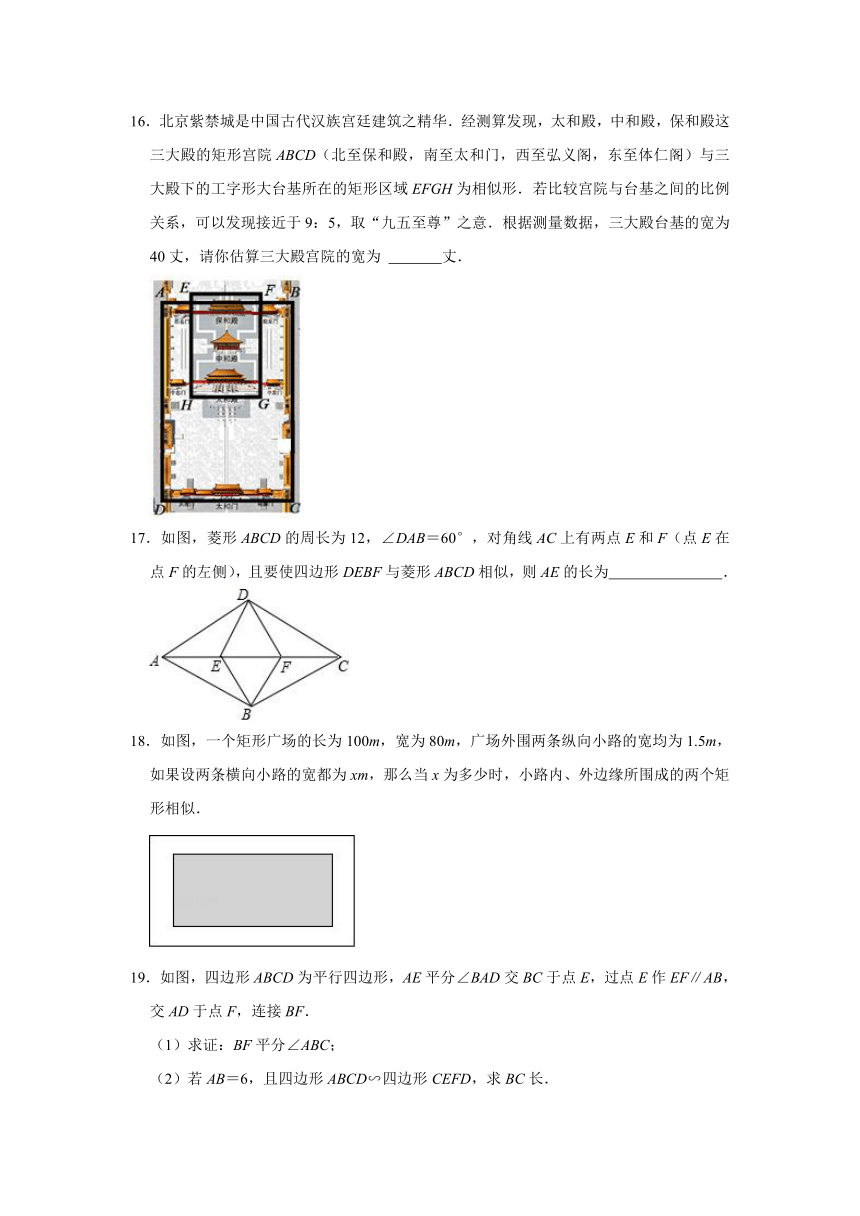
19.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
20.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
21.一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
参考答案
1.解:∵相似多边形的对应边成比例,对应角相等,
∴所有正方形都是相似多边形,
故选:C.
2.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得y:x=.
故选:A.
3.解:∵AB=1,
设AD=x,则FD=x﹣1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴=,即=,
解得:x1=,x2=(不合题意舍去),
经检验x1=是原方程的解.
∴FD=﹣1=.
故选:C.
4.解:∵原矩形的长为6,宽为x,
∴小矩形的长为x,宽为=2,
∵小矩形与原矩形相似,
∴=,
解得:x=2,
故选:B.
5.解:∵四边形ABCD是矩形,
∴AD=BC=xcm,
∵四边形ABEF是正方形,
∴EF=AB=ycm,
∴DF=EC=(x﹣y)cm,
∵矩形FDCE与原矩形ADCB相似,
∴DF:AB=CD:AD,
即:
∴=,
故选:B.
6.解:∵矩形ABCD∽矩形ECDF,
∴,设正方形ABEF的边长为x,EC=y,
则,
∴x2﹣yx﹣y2=0,
∴x=,
∵x>0,y>0,
∴x=y,
∴DF:AD=,
∵AD=2,
∴DF=3﹣,
故选:D.
7.解:∵矩形ABCD∽矩形DEFC,且面积比为4:1,
∴AB:DE=2:1,
∴设AE=x,DE=a,
∴DC=AB=2a,
则=,
整理,得:x=3a,
则=3,即AE:ED=3:1,
故选:B.
8.解:对折两次后的小长方形的长为b,宽为a,
∵小长方形与原长方形相似,
∴=,
∴a=2b.
故选:B.
9.解:由题意AD=30cm,AB=90cm,A′B′=(90+2a),A′D′=30+8=38cm,
∵矩形ABCD∽矩形A′B′C′D',
∴=,
∴=,
解得a=12,
故选:C.
10.解:根据条件可知:矩形AEFB∽矩形ABCD,
∴,
设AD=BC=x,AB=1,则AE=x.则,即:x2=1.
∴x=或﹣(舍去).
故选:C.
11.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得x:y=:1.
故答案为::1.
12.解:∵正方形EFGH与正方形ABCD的相似比为,
∴不妨假设EF=k,AB=3k,
∵∠A=∠B=∠FEH=90°,
∴∠AEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠AEH=∠EFB,
∵EH=EF,
∴△HAE≌△EBF(AAS),
∴AE=BF,设AE=BF=x则EB=3k﹣x,
在Rt△EFB中,∵EF2=BE2+BF2,
∴(k)2=(3k﹣x)2+x2,
整理得x2﹣3kx+2k2=0,
解得x=k或2k(舍弃),
∴AE=k,BE=2k,
∴=,
故答案为.
13.解:由折叠的性质可知,AB=AF=1,
∵矩形EFDC与矩形ABCD相似,
∴=,即=,
整理得,AD2﹣AD﹣1=0,
AD=,
由题意得,AD=,
故答案为:.
14.解:当=时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=1.5,
当=时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=9,
故答案为:1.5或9.
15.解:∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,
∵四边形EFDC是矩形,
∴EF=CD=2,CE=DF,
∵余下的矩形EFDC∽矩形BCDA,
∴,
即=,
∴CE=1,
故答案为:1.
16.解:设三大殿宫院的宽为x丈,
由题意得,x:40=9:5,
解得,x=72丈,
故答案为:72.
17.解:如图连接BD交AC于O.
∵四边形ABCD是菱形,周长为12,
∴AB=BC=CD=AD=3,BD⊥AC,
∵∠DAB=60°,
∴∠DAO=∠DAB=30°,
∴OD=AD=,AO=OD=,
∵四边形DEBF与菱形ABCD相似,
∴∠EDF=∠DAB=60°,
∴∠EDO=∠EDF=30°,
∴OE=OD=,
∴AE=OA﹣OE=﹣=,
故答案为.
18.解:当(100+3):100=(80+2x):80时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴,即,
解得:BC=3±3(负值舍去),
∴BC=3+3.
20.证明;∵∠GEA=∠EAF=∠GFA=90°,
∴四边形EAFG为矩形.
∵四边形ABCD为正方形,
∴AC平分∠DAB.
又∵GE⊥AD,GF⊥AB,
∴GE=GF.
∴四边形EAFG为正方形.
∴四边形AFGE与四边形ABCD相似.
21.解:(1)由已知得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,=,
∴DM BC=AB MN,即BC2=4,
∴BC=2,即它的另一边长为2;
(2)∵矩形EFDC与原矩形ABCD相似,
∴=,
∵AB=CD=2,BC=4,
∴DF==1,
∴矩形EFDC的面积=CD DF=2×1=2.
1.下列说法正确的是( )
A.所有菱形都相似 B.所有矩形都相似
C.所有正方形都相似 D.所有平行四边形都相似
2.如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( )
A. B. C. D.
3.如图,在矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的点F处,若四边形EFDC(EF>DF)与矩形ABCD相似,则DF的长为( )
A. B. C. D.1
4.矩形的两边长分别为x和6(x<6),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,则x的值为( )
A. B. C. D.2.5
5.如图,一张矩形纸片ABCD的长BC=xcm,宽AB=ycm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则的值为( )
A. B. C. D.
6.如图,在矩形ABCD中,点E、F分别在BC,AD上,四边形ABEF是正方形,矩形ABCD∽矩形ECDF,AD=2,则DF的值为( )
A. B. C. D.3
7.如图,矩形ABCD∽矩形DEFC,且面积比为4:1,则AE:ED的值为( )
A.4:1 B.3:1 C.2:1 D.3:2
8.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
9.书画经装裱后更便于收藏.如图,画心ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm.当AD与A′D′的距离、BC与B'C′距离都等于acm,且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( )
A.4 B.6 C.12 D.24
10.将一张矩形纸片ABCD沿一组对边AD和BC的中点连线EF对折,对折后所得矩形恰好与原矩形相似,若原矩形纸片的边AB=1,则BC的长为( )
A. B. C. D.2
11.如图,一张矩形纸片沿它的长边对折(EF为折痕),得到两个全等的小矩形,如果小矩形与原来的矩形相似,那么小矩形的长边与短边的比是 .
12.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则(AE<BE)的值为 .
13.如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= .
14.如图所示,矩形ABCD的长AB=30,宽BC=20,x为 时,图中的两个矩形ABCD与A'B'C'D'相似?
15.如图,矩形ABCD中,AB=2,BC=4,剪去一个矩形ABEF后,余下的矩形EFDC∽矩形BCDA,则EC的长为 .
16.北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为 丈.
17.如图,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧),且要使四边形DEBF与菱形ABCD相似,则AE的长为 .
18.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
19.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
20.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
21.一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
参考答案
1.解:∵相似多边形的对应边成比例,对应角相等,
∴所有正方形都是相似多边形,
故选:C.
2.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得y:x=.
故选:A.
3.解:∵AB=1,
设AD=x,则FD=x﹣1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴=,即=,
解得:x1=,x2=(不合题意舍去),
经检验x1=是原方程的解.
∴FD=﹣1=.
故选:C.
4.解:∵原矩形的长为6,宽为x,
∴小矩形的长为x,宽为=2,
∵小矩形与原矩形相似,
∴=,
解得:x=2,
故选:B.
5.解:∵四边形ABCD是矩形,
∴AD=BC=xcm,
∵四边形ABEF是正方形,
∴EF=AB=ycm,
∴DF=EC=(x﹣y)cm,
∵矩形FDCE与原矩形ADCB相似,
∴DF:AB=CD:AD,
即:
∴=,
故选:B.
6.解:∵矩形ABCD∽矩形ECDF,
∴,设正方形ABEF的边长为x,EC=y,
则,
∴x2﹣yx﹣y2=0,
∴x=,
∵x>0,y>0,
∴x=y,
∴DF:AD=,
∵AD=2,
∴DF=3﹣,
故选:D.
7.解:∵矩形ABCD∽矩形DEFC,且面积比为4:1,
∴AB:DE=2:1,
∴设AE=x,DE=a,
∴DC=AB=2a,
则=,
整理,得:x=3a,
则=3,即AE:ED=3:1,
故选:B.
8.解:对折两次后的小长方形的长为b,宽为a,
∵小长方形与原长方形相似,
∴=,
∴a=2b.
故选:B.
9.解:由题意AD=30cm,AB=90cm,A′B′=(90+2a),A′D′=30+8=38cm,
∵矩形ABCD∽矩形A′B′C′D',
∴=,
∴=,
解得a=12,
故选:C.
10.解:根据条件可知:矩形AEFB∽矩形ABCD,
∴,
设AD=BC=x,AB=1,则AE=x.则,即:x2=1.
∴x=或﹣(舍去).
故选:C.
11.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得x:y=:1.
故答案为::1.
12.解:∵正方形EFGH与正方形ABCD的相似比为,
∴不妨假设EF=k,AB=3k,
∵∠A=∠B=∠FEH=90°,
∴∠AEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠AEH=∠EFB,
∵EH=EF,
∴△HAE≌△EBF(AAS),
∴AE=BF,设AE=BF=x则EB=3k﹣x,
在Rt△EFB中,∵EF2=BE2+BF2,
∴(k)2=(3k﹣x)2+x2,
整理得x2﹣3kx+2k2=0,
解得x=k或2k(舍弃),
∴AE=k,BE=2k,
∴=,
故答案为.
13.解:由折叠的性质可知,AB=AF=1,
∵矩形EFDC与矩形ABCD相似,
∴=,即=,
整理得,AD2﹣AD﹣1=0,
AD=,
由题意得,AD=,
故答案为:.
14.解:当=时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=1.5,
当=时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=9,
故答案为:1.5或9.
15.解:∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,
∵四边形EFDC是矩形,
∴EF=CD=2,CE=DF,
∵余下的矩形EFDC∽矩形BCDA,
∴,
即=,
∴CE=1,
故答案为:1.
16.解:设三大殿宫院的宽为x丈,
由题意得,x:40=9:5,
解得,x=72丈,
故答案为:72.
17.解:如图连接BD交AC于O.
∵四边形ABCD是菱形,周长为12,
∴AB=BC=CD=AD=3,BD⊥AC,
∵∠DAB=60°,
∴∠DAO=∠DAB=30°,
∴OD=AD=,AO=OD=,
∵四边形DEBF与菱形ABCD相似,
∴∠EDF=∠DAB=60°,
∴∠EDO=∠EDF=30°,
∴OE=OD=,
∴AE=OA﹣OE=﹣=,
故答案为.
18.解:当(100+3):100=(80+2x):80时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴,即,
解得:BC=3±3(负值舍去),
∴BC=3+3.
20.证明;∵∠GEA=∠EAF=∠GFA=90°,
∴四边形EAFG为矩形.
∵四边形ABCD为正方形,
∴AC平分∠DAB.
又∵GE⊥AD,GF⊥AB,
∴GE=GF.
∴四边形EAFG为正方形.
∴四边形AFGE与四边形ABCD相似.
21.解:(1)由已知得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,=,
∴DM BC=AB MN,即BC2=4,
∴BC=2,即它的另一边长为2;
(2)∵矩形EFDC与原矩形ABCD相似,
∴=,
∵AB=CD=2,BC=4,
∴DF==1,
∴矩形EFDC的面积=CD DF=2×1=2.
同课章节目录
