2.3等腰三角形的判定

(共20张PPT)
2.3 等腰三角形的判定
义务教育课程标准实验教科书　
浙江版《数学》八年级上册
等腰三角形的性质:
复习回顾:
2、等腰三角形的两个底角相等.
(在同一个三角形中,等边对等角)
1、等腰三角形的两腰相等.
3、等腰三角形三线合一
顶角平分线、底边上的中线 和底边上的高
等腰三角形的判定方法：
1、有两边相等的三角形是等腰三角形。
如图，在ΔABC中，∠B=∠C，判断AB和AC是否相等，并说明理由。
A
C
B
D
合作学习:
在ΔABD和ΔACD中
∠B=∠C
∠ADB=∠ADC=90°
AD=AD
∴ΔABD≌ΔACD(AAS)
∴AB=AC
“在同一个三角形中,等角对等边。”
2、如果一个三角形有两个角相等，那么这个三角形是等腰三角形．
等腰三角形的判定方法：
“在同一个三角形中, 等边对等角。”
辨一辨：
1、有两边相等的三角形是等腰三角形。
性质
判定
在同一个三角形中,
等角对等边
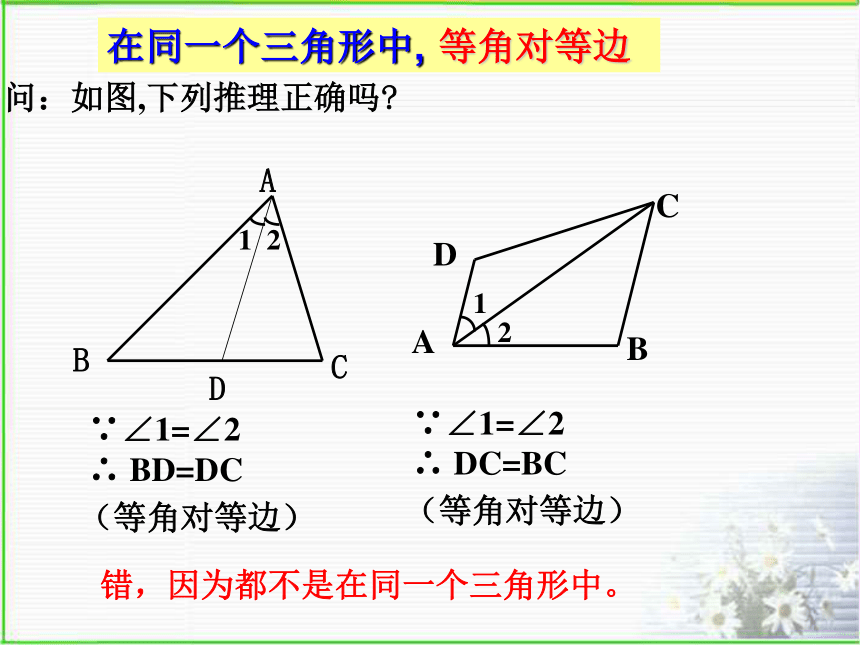
问：如图,下列推理正确吗
A
B
C
D
2
1
∵∠1=∠2 ∴ BD=DC
（等角对等边）
∵∠1=∠2 ∴ DC=BC
A
B
C
D
2
1
（等角对等边）
错，因为都不是在同一个三角形中。
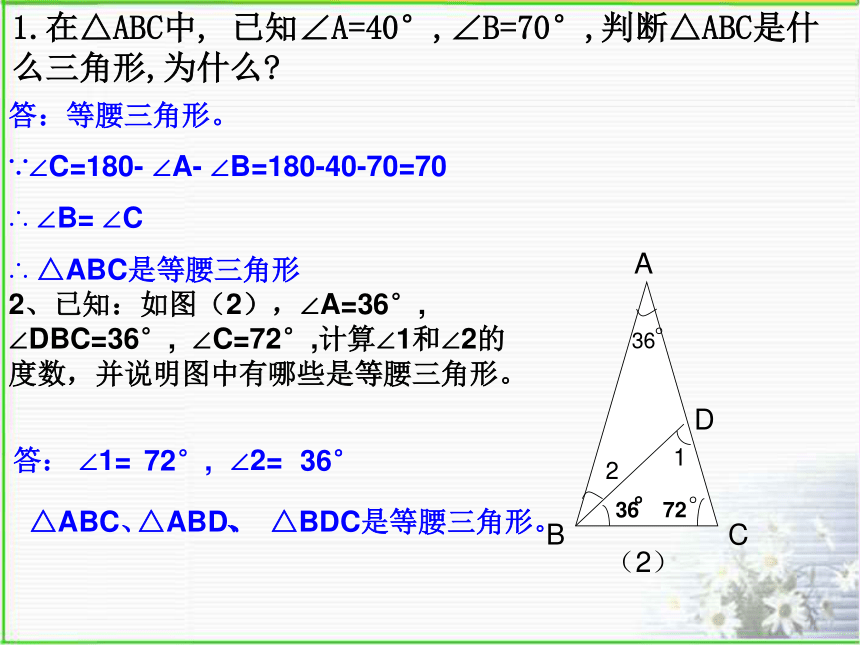
1.在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
答：等腰三角形。
∵∠C=180- ∠A- ∠B=180-40-70=70
∴ ∠B= ∠C
∴ △ABC是等腰三角形
2、已知：如图（2），∠A=36°, ∠DBC=36°, ∠C=72°,计算∠1和∠2的度数，并说明图中有哪些是等腰三角形。
A
B
C
D
36
°
1
2
36
°
°
72
答： ∠1=
72°,
∠2=
36°
△ABC、
△ABD、
、 △BDC
是等腰三角形。
（2）
例1：一次数学实践活动的内容是测量河宽，如图，即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是：从点Ａ出发,沿着与直线AB成60°角的AC方向前进至C，在C处测得∠C＝30°.量出AC的长，它就是河宽（即A,B之间的距离）．这个方法正确吗？请说明理由．
说明线段相等的方法:
1、说明线段所在的两个三角形全等。
2、说明同一个三角形中线段所对的
两个角相等。
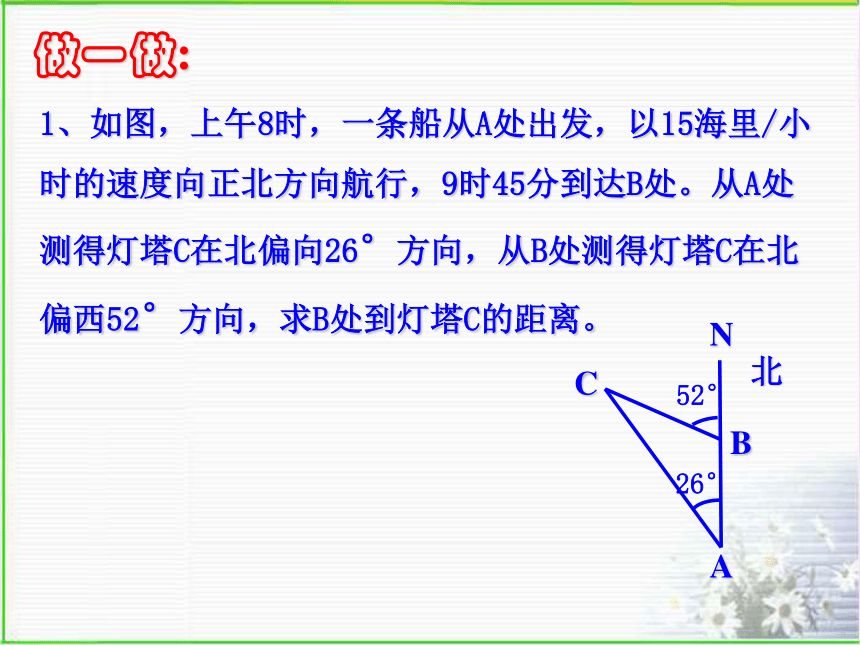
1、如图，上午8时，一条船从A处出发，以15海里/小时的速度向正北方向航行，9时45分到达B处。从A处测得灯塔C在北偏向26°方向，从B处测得灯塔C在北偏西52°方向，求B处到灯塔C的距离。
N
B
A
C
52°
26°
北
做一做:
如图，在△ABC中，AB=AC，∠1=∠2，则△ABD和△ACD全等吗？为什么？
A
C
B
D
1 2
做一做:
例2:如图，AD平分△ABC的外角∠EAC，AD//BC，则△ ABC是等腰三角形吗？说明你的理由。
证明：∵AD∥BC，
A
E
B
C
1
2
D
∴∠1=∠B（两直线平行，同位角相等）
∠2=∠C（两直线平行，内错角相等）
∵ ∠1=∠2，
∴∠B=∠C
∴AB=AC（等角对等边）
例3：如图，BD是等腰三角形ABC的底边AC上的高，DE∥BC，交AB于点E。判断△BDE是不是等腰三角形，并说明理由。
B
C
A
D
1
2
3
┏
E
在△ABC中,已知 AB =AC ,BG平分∠ABC,CG平分∠ACB.过点G作直线EF//BC交AB于E,交AC于F.
（1）请问图中有多少个等腰三角形 说明理由.
（2）线段EF和线段EB,FC之间有没有关系 若有是
什么关系
F
E
G
B
C
A
B
G
C
A
E
F
AB≠AC
思考探究
EF=BE+FC
已知：如图（10），∠1=∠2， ∠3=∠4，DE∥BC;
求证：DE=DB+EC。
A
B
D
C
E
F
1
2
3
4
（10）
证明：
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2，∠3=∠4
∴∠1=∠DFB，∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC
F
E
G
B
C
A
在△ABC中,已知 AB =AC ,BG平
分∠ABC,CG平分∠ACB.过点G
作直线EF//BC交AB于E,交AC于F.
已知BE+FC=5，则EF=______
5
已知:如图,在△ABC中，BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,求: △ODE的周长
△ODE的周长=BC=16
如图，在△ABC中，D，E分别是AC，AB上的点，BD，CE相交于
点O。若∠BEO=∠CDO，BE=CD，
问△ABC是等腰三角形吗？
请说明理由。
B
A
C
D
E
O
做一做:
只要证明△BEO ≌△DCO就能说明△ABC是等腰三角形
名称 图 形 概念 性 质 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
说能出你这节课的收获和体验让大家与你分享吗？
请把这个三角形纸片折成两个等腰三角形！
A
C
B
50°
110°
20°
1、对∠A进行讨论
2、对∠B进行讨论
3、对∠C进行讨论
C
A
B
A
C
B
20°
20°
20°
20°
C
A
B
50°
50°
C
A
B
80°
80°
20°
C
A
B
65°
65°
50°
C
A
B
35°
35°
110°
（分类讨论）
A
C
B
50°
110°
20°