4.2由平行线截得的比例线段 同步测评 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.2由平行线截得的比例线段 同步测评 2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 19:39:33 | ||
图片预览



文档简介
2021-2022学年浙教版九年级数学上册《4.2由平行线截得的比例线段》同步测评(附答案)
一.选择题(共8小题,满分40分)
1.如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
2.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
3.AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A.1:3 B.1:4 C.1:5 D.1:6
4.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F,若=,DE=6,则EF的长是( )
A.9 B.10 C.2 D.15
5.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC长是( )
A.4 B. C.2.5 D.4.5
6.如图l1∥l2∥l3,若=,DF=10,则DE=( )
A.4 B.6 C.8 D.9
7.在△ABC中,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,若BD=2AD,则的值为( )
A. B. C. D.
8.如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为( )
A.3 B. C.4 D.
二.填空题(共8小题,满分40分)
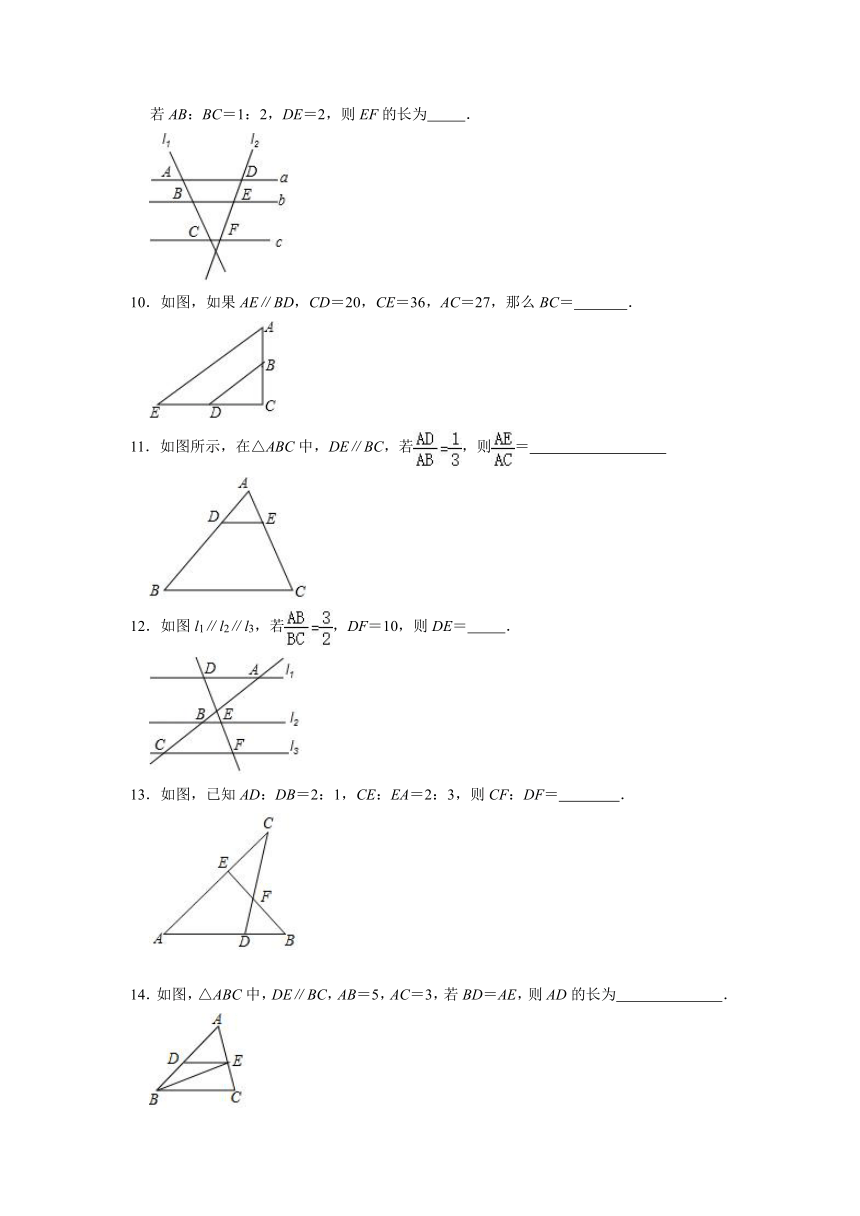
9.如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,若AB:BC=1:2,DE=2,则EF的长为 .
10.如图,如果AE∥BD,CD=20,CE=36,AC=27,那么BC= .
11.如图所示,在△ABC中,DE∥BC,若,则=
12.如图l1∥l2∥l3,若,DF=10,则DE= .
13.如图,已知AD:DB=2:1,CE:EA=2:3,则CF:DF= .
14.如图,△ABC中,DE∥BC,AB=5,AC=3,若BD=AE,则AD的长为 .
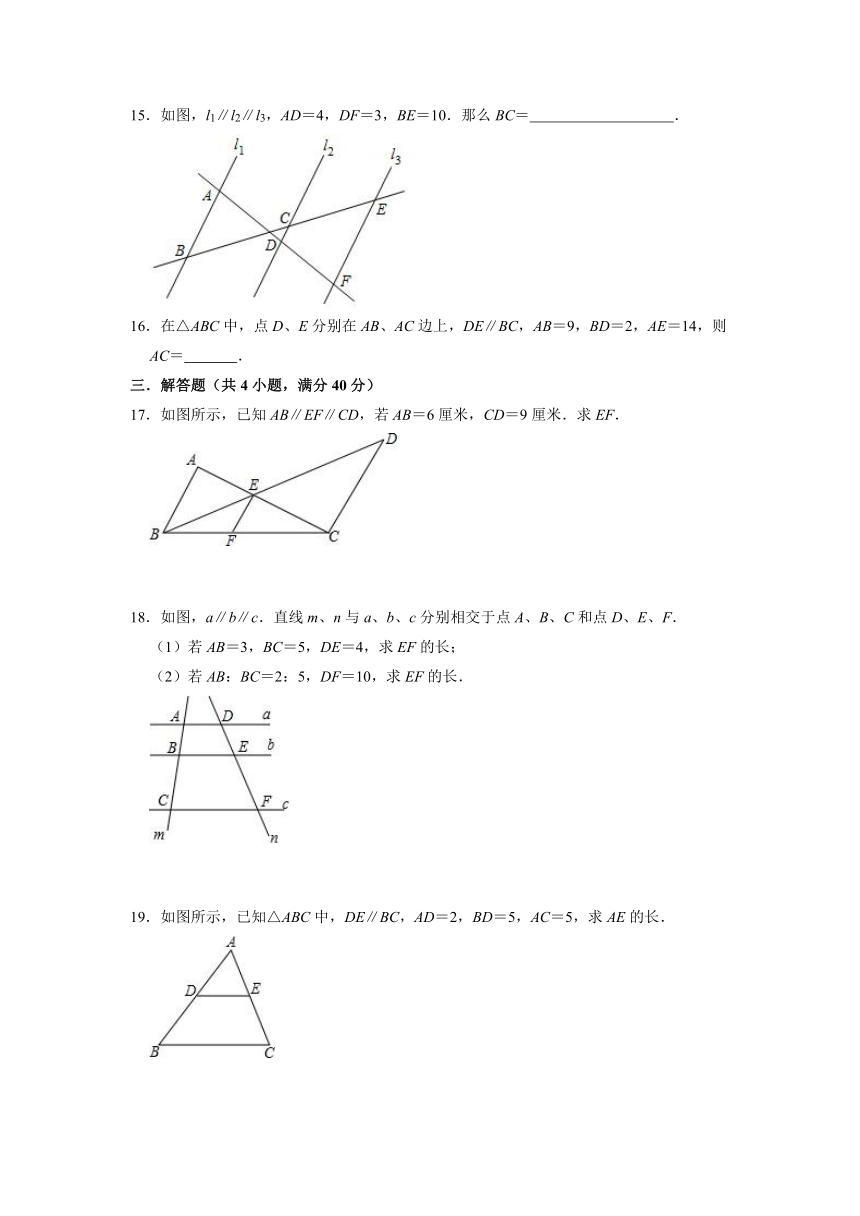
15.如图,l1∥l2∥l3,AD=4,DF=3,BE=10.那么BC= .
16.在△ABC中,点D、E分别在AB、AC边上,DE∥BC,AB=9,BD=2,AE=14,则AC= .
三.解答题(共4小题,满分40分)
17.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
18.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长.
19.如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长.
20.已知:如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,DE∥AC,DF∥BC.如果BE=6cm,EC=10cm,AF﹣FC=3cm,求FC的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵l1∥l2∥l3,
∴=,A错误;
=,B错误;
≠,C错误;
=,D正确.
故选:D.
2.解:∵AD∥BE∥CF,
∴=,
∵AB=3,BC=6,DE=2,
∴EF==4,
故选:C.
3.解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴==,
∴AF:FC=1:6,
故选:D.
4.解:∵l1∥l2∥l3,
∴=,即=,
解得:DF=15,
∴EF=15﹣6=9.
故选:A.
5.解:∵DE∥AC,
∴DB:AB=BE:BC,
∵DB=4,AB=6,BE=3,
∴4:6=3:BC,
解得:BC=,
∴EC=BC﹣BE=.
故选:B.
6.解:l1∥l2∥l3,
∴==,
又∵DF=10,
∴DE=DF=6,
故选:B.
7.解:∵DE∥AC,EF∥AB,BD=2AD,
∴,
故选:A.
8.解:∵DE∥BC,
∴=,
∴=,
∴EC=4,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵a∥b∥c,
∴,
∵DE=2,
∴EF=4,
故答案为:4
10.解:∵AE∥BD,CD=20,CE=36,AC=27,
∴,
即,
解得:BC=15,
故答案为:15
11.解:∵在△ABC中,DE∥BC,,
∴,
故答案为:
12.解:∵l1∥l2∥l3,,
∴==,
∵DF=10,
∴=,
解得:DE=6,
故答案为:6.
13.解:过D作DM∥AC,交BE于M,
∵DM∥AC,
∴△BMD∽△BEA,
∴=,
∵AD:DB=2:1,
∴===,
即AE=3DM,
∵CE:EA=2:3,
∴CE=2DM,
∵DM∥AC,
∴△DMF∽△CEF,
∴===,
故答案为:2:1.
14.解:由题意得AE=BD=AB﹣AD=5﹣AD,
∵DE∥BC,
∴=,即=,
解得,AD=,
故答案为:.
15.解:∵l1∥l2∥l3,
∴=,
∵AD=4,DF=3,BE=10,
∴=,
解得:BC=,
故答案为:.
16.解:∵DE∥BC,
∴=,即=,
解得,AC=18,
故答案为:18.
三.解答题(共4小题,满分40分)
17.解:在△ABC中,因为EF∥AB,
所以=①,
同样,在△DBC中有=②,
①+②得+=+=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
+=1,
解得x=.
故EF=厘米.
18.解:(1)∵a∥b∥c,
∴,即,
解得;
(2)∵a∥b∥c,
∴,
∴,
解得.
19.解:∵DE∥BC,
∴,即=,
∴AE=.
20.解:∵DE∥AC,BE=6cm,EC=10cm,
∴BD:DA=BE:EC=6:10=3:5,
又∵DF∥BC,
∴CF:FA=BD:DA=3:5,
而AF﹣FC=3cm,
∴AF=FC+3,
∴CF:(FC+3)=3:5,
∴CF=4.5 cm.
一.选择题(共8小题,满分40分)
1.如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A. B. C. D.
2.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
3.AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )
A.1:3 B.1:4 C.1:5 D.1:6
4.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F,若=,DE=6,则EF的长是( )
A.9 B.10 C.2 D.15
5.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC,若DB=4,AB=6,BE=3,则EC长是( )
A.4 B. C.2.5 D.4.5
6.如图l1∥l2∥l3,若=,DF=10,则DE=( )
A.4 B.6 C.8 D.9
7.在△ABC中,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,若BD=2AD,则的值为( )
A. B. C. D.
8.如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为( )
A.3 B. C.4 D.
二.填空题(共8小题,满分40分)
9.如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,若AB:BC=1:2,DE=2,则EF的长为 .
10.如图,如果AE∥BD,CD=20,CE=36,AC=27,那么BC= .
11.如图所示,在△ABC中,DE∥BC,若,则=
12.如图l1∥l2∥l3,若,DF=10,则DE= .
13.如图,已知AD:DB=2:1,CE:EA=2:3,则CF:DF= .
14.如图,△ABC中,DE∥BC,AB=5,AC=3,若BD=AE,则AD的长为 .
15.如图,l1∥l2∥l3,AD=4,DF=3,BE=10.那么BC= .
16.在△ABC中,点D、E分别在AB、AC边上,DE∥BC,AB=9,BD=2,AE=14,则AC= .
三.解答题(共4小题,满分40分)
17.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
18.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长.
19.如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长.
20.已知:如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,DE∥AC,DF∥BC.如果BE=6cm,EC=10cm,AF﹣FC=3cm,求FC的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵l1∥l2∥l3,
∴=,A错误;
=,B错误;
≠,C错误;
=,D正确.
故选:D.
2.解:∵AD∥BE∥CF,
∴=,
∵AB=3,BC=6,DE=2,
∴EF==4,
故选:C.
3.解:作DH∥BF交AC于H,
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴==,
∴AF:FC=1:6,
故选:D.
4.解:∵l1∥l2∥l3,
∴=,即=,
解得:DF=15,
∴EF=15﹣6=9.
故选:A.
5.解:∵DE∥AC,
∴DB:AB=BE:BC,
∵DB=4,AB=6,BE=3,
∴4:6=3:BC,
解得:BC=,
∴EC=BC﹣BE=.
故选:B.
6.解:l1∥l2∥l3,
∴==,
又∵DF=10,
∴DE=DF=6,
故选:B.
7.解:∵DE∥AC,EF∥AB,BD=2AD,
∴,
故选:A.
8.解:∵DE∥BC,
∴=,
∴=,
∴EC=4,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵a∥b∥c,
∴,
∵DE=2,
∴EF=4,
故答案为:4
10.解:∵AE∥BD,CD=20,CE=36,AC=27,
∴,
即,
解得:BC=15,
故答案为:15
11.解:∵在△ABC中,DE∥BC,,
∴,
故答案为:
12.解:∵l1∥l2∥l3,,
∴==,
∵DF=10,
∴=,
解得:DE=6,
故答案为:6.
13.解:过D作DM∥AC,交BE于M,
∵DM∥AC,
∴△BMD∽△BEA,
∴=,
∵AD:DB=2:1,
∴===,
即AE=3DM,
∵CE:EA=2:3,
∴CE=2DM,
∵DM∥AC,
∴△DMF∽△CEF,
∴===,
故答案为:2:1.
14.解:由题意得AE=BD=AB﹣AD=5﹣AD,
∵DE∥BC,
∴=,即=,
解得,AD=,
故答案为:.
15.解:∵l1∥l2∥l3,
∴=,
∵AD=4,DF=3,BE=10,
∴=,
解得:BC=,
故答案为:.
16.解:∵DE∥BC,
∴=,即=,
解得,AC=18,
故答案为:18.
三.解答题(共4小题,满分40分)
17.解:在△ABC中,因为EF∥AB,
所以=①,
同样,在△DBC中有=②,
①+②得+=+=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
+=1,
解得x=.
故EF=厘米.
18.解:(1)∵a∥b∥c,
∴,即,
解得;
(2)∵a∥b∥c,
∴,
∴,
解得.
19.解:∵DE∥BC,
∴,即=,
∴AE=.
20.解:∵DE∥AC,BE=6cm,EC=10cm,
∴BD:DA=BE:EC=6:10=3:5,
又∵DF∥BC,
∴CF:FA=BD:DA=3:5,
而AF﹣FC=3cm,
∴AF=FC+3,
∴CF:(FC+3)=3:5,
∴CF=4.5 cm.
同课章节目录
