4.4两个相似三角形的判定同步测评 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.4两个相似三角形的判定同步测评 2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 339.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 19:44:58 | ||
图片预览


文档简介
2021-2022学年浙教版九年级数学上册《4.4两个相似三角形的判定》同步测评(附答案)
一.选择题(共10小题,满分50分)
1.如图,△ABC中,DE∥BC,EF∥AB,则下列式子正确的是( )
A.= B.= C.= D.=
2.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC:BD=3:4,AE⊥CD于点E,则AE的长是( )
A.4 B. C.5 D.
3.在⊙O中,AB,CD是互相垂直的两条直径,点E在上,CF⊥AE于点F.若点F三等分弦AE,⊙O的直径为12,则CF的长是( )
A. B. C. D.
4.如图,在△ABC中,DE∥BC,若S△ADE:S△BDE=1:2,S△ADE=3,则S△ABC为( )
A.9 B.12 C.24 D.27
5.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A. B. C. D.
6.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,那么△DEF的周长与△BAF的周长之比为( )
A.3:4 B.9:16 C.1:3 D.3:2
7.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=DH;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
8.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 ( )
A. B. C. D.
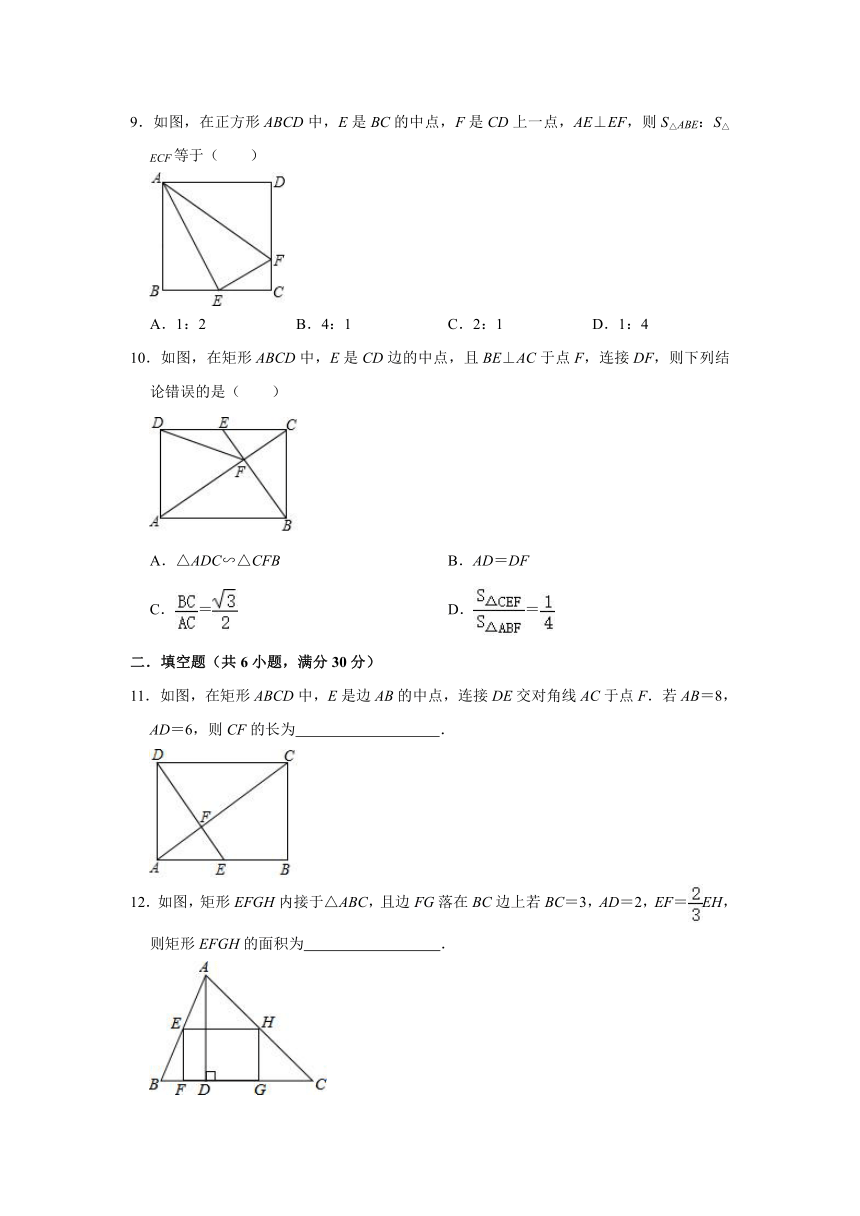
9.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则S△ABE:S△ECF等于( )
A.1:2 B.4:1 C.2:1 D.1:4
10.如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
A.△ADC∽△CFB B.AD=DF
C.= D.=
二.填空题(共6小题,满分30分)
11.如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F.若AB=8,AD=6,则CF的长为 .
12.如图,矩形EFGH内接于△ABC,且边FG落在BC边上若BC=3,AD=2,EF=EH,则矩形EFGH的面积为 .
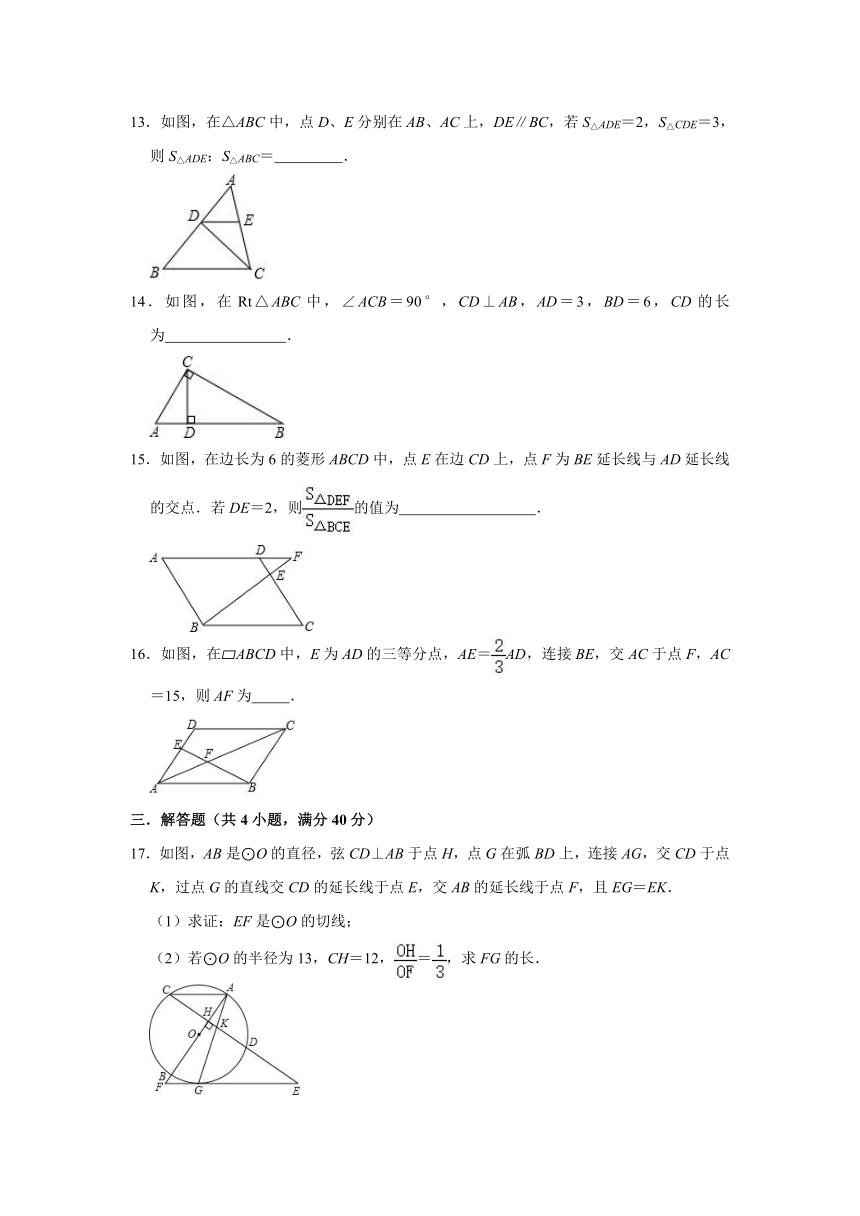
13.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若S△ADE=2,S△CDE=3,则S△ADE:S△ABC= .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AD=3,BD=6,CD的长为 .
15.如图,在边长为6的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=2,则的值为 .
16.如图,在 ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=15,则AF为 .
三.解答题(共4小题,满分40分)
17.如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD的延长线于点E,交AB的延长线于点F,且EG=EK.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,=,求FG的长.
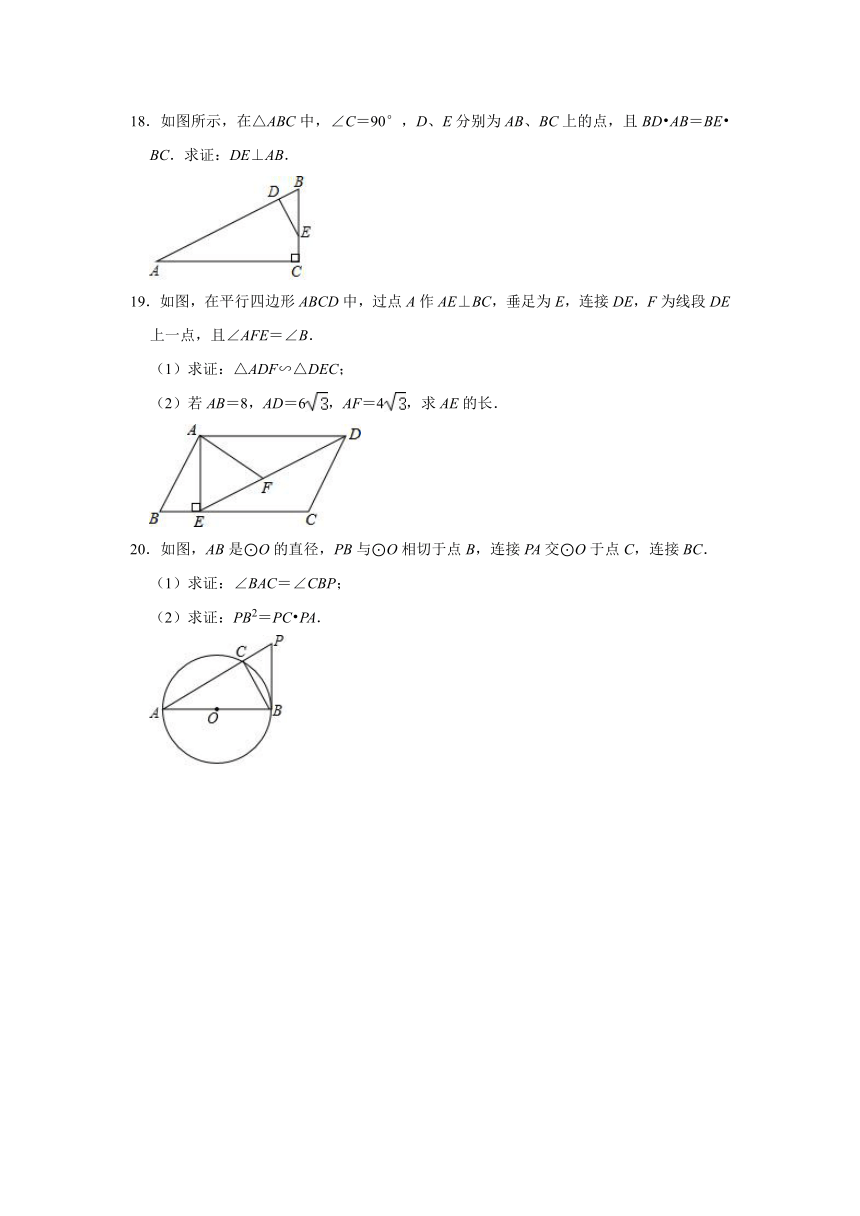
18.如图所示,在△ABC中,∠C=90°,D、E分别为AB、BC上的点,且BD AB=BE BC.求证:DE⊥AB.
19.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
20.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC PA.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵DE∥BC,
∴=,
∵EF∥AB,
∴=,
∴=,故A选项正确;
∵DE∥BC,
∴=,故B选项错误;
∵DE∥BC,EF∥AB,
∴=,=,
∴≠,故C选项错误;
而=不成立,故D选项错误;
故选:A.
2.解:∵四边形ABCD是菱形,
∴AO=AC,OB=BD,AC⊥BD,
∵AC:BD=3:4,
∴AO:OB=3:4,
设AO=3x,OB=4x,则AB=5x,
∵AB=5,
∴5x=5,x=1,
∴AC=6,BD=8,
S菱形ABCD=,
∴,
AE=,
故选:B.
3.解:如图,连接AC,EC.设AE交OC于点K,设EF=a.
∵AF=2EF,EF=a,
∴AF=2a,
∵AB⊥CD,
∴∠AOC=90°,
∴∠CEA=∠AOC=45°,
∵CF⊥EF,
∴∠CFE=90°,
∴∠FCE=∠FEC=45°,
∴CF=EF=a,
∴AC==a,
∵OA=OC=6,
∴AC=6,
∴a=6,
∴a=
∴CF=
故选:D.
4.解:∵S△ADE:S△BDE=1:2,
∴AD:BD=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴=()2=,
∵S△ADE=3,
∴S△ABC=27,
故选:D.
5.解:∵DE∥BC,
∴△ADE∽△ABC,△AEG∽△ACF,△AGD∽△AFB,=,故B错误.
∴=,==,=,
∴A错误,C正确,D错误.
故选:C.
6.解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴C△DFE:C△BFA=3:4.
故选:A.
7.解:∵四边形ABCD是正方形,
∴AB=BC=CD,
∵AG=CE,
∴BG=BE,
∴∠BEG=45°,
∴∠BEA>45°,
∵∠AEF=90°,
∴∠HEC<45°,
则HC<EC,
∴CD﹣CH>BC﹣CE,即DH>BE,故①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中,
∵
∴△GAE≌△CEF(SAS),∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
故选:C.
8.解:作AH⊥BC于H,交GF于M,如图,
∵△ABC的面积是6,
∴BC AH=6,
∴AH==3,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,
∵GF∥BC,
∴△AGF∽△ABC,
∴=,即=,解得x=,
即正方形DEFG的边长为.
故选:A.
9.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴△BAE∽△CEF,
∴S△ABE:S△ECF=AB2:CE2,
∵E是BC的中点,
∴BC=2CE=AB
∴==,即S△ABE:S△ECF=4:1
故选:B.
10.解:∵BE⊥AC,∠ADC=∠BCD=90°,
∴∠BCF+∠ACD=∠CAD+∠ACD,
∴∠CAD=∠BCF,
∴△ADC∽△CFB,故A选项正确;
如图,过D作DM∥BE交AC于N,交AB于M,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=DC,
∴BM=AM,
∴AN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥AF,
∴DM垂直平分AF,
∴DF=DA,故B选项正确;
设CE=a,AD=b,则CD=2a,
由△ADC∽△ECB,可得=,
即b=a,
∴,
∴=,故C选项错误;
∵E是CD边的中点,
∴CE:AB=1:2,
又∵CE∥AB,
∴△CEF∽△ABF,
∴=()2=,故选D选项正确;
故选:C.
二.填空题(共6小题,满分30分)
11.解:在Rt△ABC中,AB=8,BC=AD=6,∠B=90°,
∴AC==10.
∵AB∥CD,
∴∠DCF=∠EAF,∠CDF=∠AEF,
∴△AEF∽△CDF,
∴=.
又∵E是边AB的中点,
∴CD=AB=2AE,
∴=2,
∴CF=2AF.
∵AC=AF+CD=10,
∴CF=AC=.
故答案为:.
12.解:∵EF⊥FG,AD⊥BC
∴AD∥EF
∴=,
∵EH∥BC
∴=,
∴+=+,且BC=3,AD=2,EF=EH.
∴=1=+
∴EH=,
则EF=1
∴矩形EFGH的面积=EF×EH=,
故答案为:.
13.解:∵△ADE的边AE上的高和△CDE的边CE上的高相等,
又∵S△ADE=2,S△CDE=3,
∴=,
∵DE∥BC,
∴=,
∴S△ADE:S△ABC=()2=.
故答案为:4:25.
14.解:由射影定理得,CD2=AD BD=18,
解得,CD=3,
故答案为:3.
15.解:∵DE=2,DC=6,
∴EC=DC﹣DE=4,
∵四边形ABCD是菱形,
∴AD∥BC,
∴△DEF∽△CEB,
∴=()2=,
故答案为:.
16.解:在 ABCD中,AD=BC,AD∥BC,
∵E为AD的三等分点,
∴AE=AD=BC,
∵AD∥BC,
∴==,
∵AC=15,
∴AF=×15=6.
故答案为6.
三.解答题(共4小题,满分40分)
17.(1)证明:连接OG,
∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线;
(2)解:连接CO,在Rt△OHC中,
∵CO=13,CH=12,
∴HO=5,
∴AH=8,
∵=,
∴OF=15,
∴FG===2.
18.证明:∵BD AB=BE BC,
∴=,又∠DBE=∠CBA,
∴△BDE∽△BCA,
∴∠BDE=∠C=90°,即DE⊥AB.
19.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
20.解:(1)∵AB是⊙O的直径,PB与⊙O相切于点B,
∴∠ACB=∠ABP=90°,
∴∠A+∠ABC=∠ABC+∠CBP=90°,
∴∠BAC=∠CBP;
(2)∵∠PCB=∠ABP=90°,
∠P=∠P,
∴△ABP∽△BCP,
∴=,
∴PB2=PC PA;
一.选择题(共10小题,满分50分)
1.如图,△ABC中,DE∥BC,EF∥AB,则下列式子正确的是( )
A.= B.= C.= D.=
2.如图,在菱形ABCD中,AB=5,对角线AC与BD相交于点O,且AC:BD=3:4,AE⊥CD于点E,则AE的长是( )
A.4 B. C.5 D.
3.在⊙O中,AB,CD是互相垂直的两条直径,点E在上,CF⊥AE于点F.若点F三等分弦AE,⊙O的直径为12,则CF的长是( )
A. B. C. D.
4.如图,在△ABC中,DE∥BC,若S△ADE:S△BDE=1:2,S△ADE=3,则S△ABC为( )
A.9 B.12 C.24 D.27
5.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A. B. C. D.
6.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,那么△DEF的周长与△BAF的周长之比为( )
A.3:4 B.9:16 C.1:3 D.3:2
7.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=DH;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
8.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 ( )
A. B. C. D.
9.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则S△ABE:S△ECF等于( )
A.1:2 B.4:1 C.2:1 D.1:4
10.如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
A.△ADC∽△CFB B.AD=DF
C.= D.=
二.填空题(共6小题,满分30分)
11.如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F.若AB=8,AD=6,则CF的长为 .
12.如图,矩形EFGH内接于△ABC,且边FG落在BC边上若BC=3,AD=2,EF=EH,则矩形EFGH的面积为 .
13.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若S△ADE=2,S△CDE=3,则S△ADE:S△ABC= .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AD=3,BD=6,CD的长为 .
15.如图,在边长为6的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=2,则的值为 .
16.如图,在 ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=15,则AF为 .
三.解答题(共4小题,满分40分)
17.如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD的延长线于点E,交AB的延长线于点F,且EG=EK.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,=,求FG的长.
18.如图所示,在△ABC中,∠C=90°,D、E分别为AB、BC上的点,且BD AB=BE BC.求证:DE⊥AB.
19.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
20.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC PA.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵DE∥BC,
∴=,
∵EF∥AB,
∴=,
∴=,故A选项正确;
∵DE∥BC,
∴=,故B选项错误;
∵DE∥BC,EF∥AB,
∴=,=,
∴≠,故C选项错误;
而=不成立,故D选项错误;
故选:A.
2.解:∵四边形ABCD是菱形,
∴AO=AC,OB=BD,AC⊥BD,
∵AC:BD=3:4,
∴AO:OB=3:4,
设AO=3x,OB=4x,则AB=5x,
∵AB=5,
∴5x=5,x=1,
∴AC=6,BD=8,
S菱形ABCD=,
∴,
AE=,
故选:B.
3.解:如图,连接AC,EC.设AE交OC于点K,设EF=a.
∵AF=2EF,EF=a,
∴AF=2a,
∵AB⊥CD,
∴∠AOC=90°,
∴∠CEA=∠AOC=45°,
∵CF⊥EF,
∴∠CFE=90°,
∴∠FCE=∠FEC=45°,
∴CF=EF=a,
∴AC==a,
∵OA=OC=6,
∴AC=6,
∴a=6,
∴a=
∴CF=
故选:D.
4.解:∵S△ADE:S△BDE=1:2,
∴AD:BD=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴=()2=,
∵S△ADE=3,
∴S△ABC=27,
故选:D.
5.解:∵DE∥BC,
∴△ADE∽△ABC,△AEG∽△ACF,△AGD∽△AFB,=,故B错误.
∴=,==,=,
∴A错误,C正确,D错误.
故选:C.
6.解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴C△DFE:C△BFA=3:4.
故选:A.
7.解:∵四边形ABCD是正方形,
∴AB=BC=CD,
∵AG=CE,
∴BG=BE,
∴∠BEG=45°,
∴∠BEA>45°,
∵∠AEF=90°,
∴∠HEC<45°,
则HC<EC,
∴CD﹣CH>BC﹣CE,即DH>BE,故①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中,
∵
∴△GAE≌△CEF(SAS),∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
故选:C.
8.解:作AH⊥BC于H,交GF于M,如图,
∵△ABC的面积是6,
∴BC AH=6,
∴AH==3,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,
∵GF∥BC,
∴△AGF∽△ABC,
∴=,即=,解得x=,
即正方形DEFG的边长为.
故选:A.
9.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴△BAE∽△CEF,
∴S△ABE:S△ECF=AB2:CE2,
∵E是BC的中点,
∴BC=2CE=AB
∴==,即S△ABE:S△ECF=4:1
故选:B.
10.解:∵BE⊥AC,∠ADC=∠BCD=90°,
∴∠BCF+∠ACD=∠CAD+∠ACD,
∴∠CAD=∠BCF,
∴△ADC∽△CFB,故A选项正确;
如图,过D作DM∥BE交AC于N,交AB于M,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=DC,
∴BM=AM,
∴AN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥AF,
∴DM垂直平分AF,
∴DF=DA,故B选项正确;
设CE=a,AD=b,则CD=2a,
由△ADC∽△ECB,可得=,
即b=a,
∴,
∴=,故C选项错误;
∵E是CD边的中点,
∴CE:AB=1:2,
又∵CE∥AB,
∴△CEF∽△ABF,
∴=()2=,故选D选项正确;
故选:C.
二.填空题(共6小题,满分30分)
11.解:在Rt△ABC中,AB=8,BC=AD=6,∠B=90°,
∴AC==10.
∵AB∥CD,
∴∠DCF=∠EAF,∠CDF=∠AEF,
∴△AEF∽△CDF,
∴=.
又∵E是边AB的中点,
∴CD=AB=2AE,
∴=2,
∴CF=2AF.
∵AC=AF+CD=10,
∴CF=AC=.
故答案为:.
12.解:∵EF⊥FG,AD⊥BC
∴AD∥EF
∴=,
∵EH∥BC
∴=,
∴+=+,且BC=3,AD=2,EF=EH.
∴=1=+
∴EH=,
则EF=1
∴矩形EFGH的面积=EF×EH=,
故答案为:.
13.解:∵△ADE的边AE上的高和△CDE的边CE上的高相等,
又∵S△ADE=2,S△CDE=3,
∴=,
∵DE∥BC,
∴=,
∴S△ADE:S△ABC=()2=.
故答案为:4:25.
14.解:由射影定理得,CD2=AD BD=18,
解得,CD=3,
故答案为:3.
15.解:∵DE=2,DC=6,
∴EC=DC﹣DE=4,
∵四边形ABCD是菱形,
∴AD∥BC,
∴△DEF∽△CEB,
∴=()2=,
故答案为:.
16.解:在 ABCD中,AD=BC,AD∥BC,
∵E为AD的三等分点,
∴AE=AD=BC,
∵AD∥BC,
∴==,
∵AC=15,
∴AF=×15=6.
故答案为6.
三.解答题(共4小题,满分40分)
17.(1)证明:连接OG,
∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线;
(2)解:连接CO,在Rt△OHC中,
∵CO=13,CH=12,
∴HO=5,
∴AH=8,
∵=,
∴OF=15,
∴FG===2.
18.证明:∵BD AB=BE BC,
∴=,又∠DBE=∠CBA,
∴△BDE∽△BCA,
∴∠BDE=∠C=90°,即DE⊥AB.
19.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
20.解:(1)∵AB是⊙O的直径,PB与⊙O相切于点B,
∴∠ACB=∠ABP=90°,
∴∠A+∠ABC=∠ABC+∠CBP=90°,
∴∠BAC=∠CBP;
(2)∵∠PCB=∠ABP=90°,
∠P=∠P,
∴△ABP∽△BCP,
∴=,
∴PB2=PC PA;
同课章节目录
