4.7图形的位似 同步达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.7图形的位似 同步达标测评 2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 19:46:12 | ||
图片预览

文档简介
2021-2022学年浙教版九年级数学上册《4.7图形的位似》同步达标测评(附答案)
一.选择题(共11小题,满分44分)
1.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
2.用位似方法把图形扩大或缩小时,下列说法中,正确的是( )
A.位似中心要么取在图形外部,要么取在图形内部
B.位似中心取在图形内部时,只能把图形缩小
C.当位似中心确定后,按要求放大或缩小的图形只能画一个
D.以上说法都不正确
3.如图,在平面直角坐标系xOy中,正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,点A,B,E在x轴上,若正方形BEFG的边长为12,则点C的坐标为( )
A.(6,2) B.(6,4) C.(4,4) D.(8,4)
4.如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
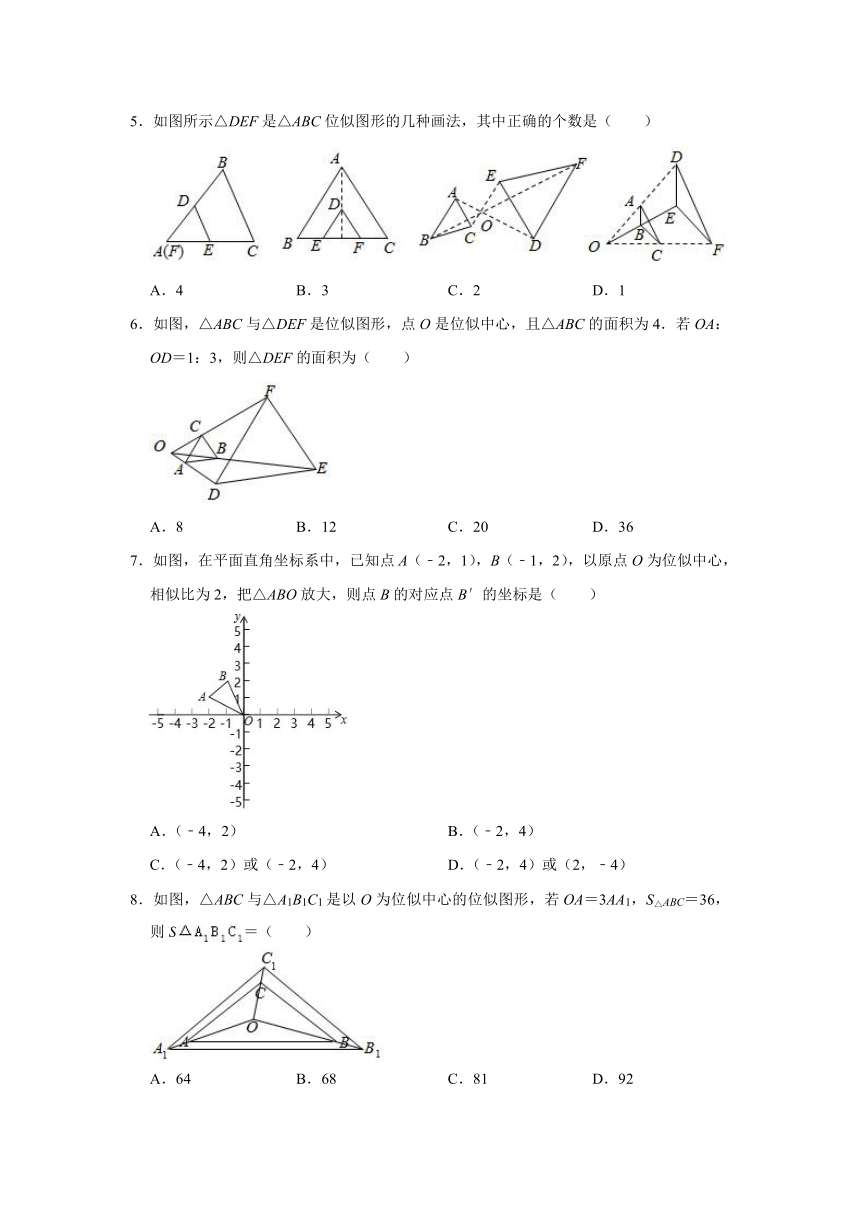
5.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是( )
A.4 B.3 C.2 D.1
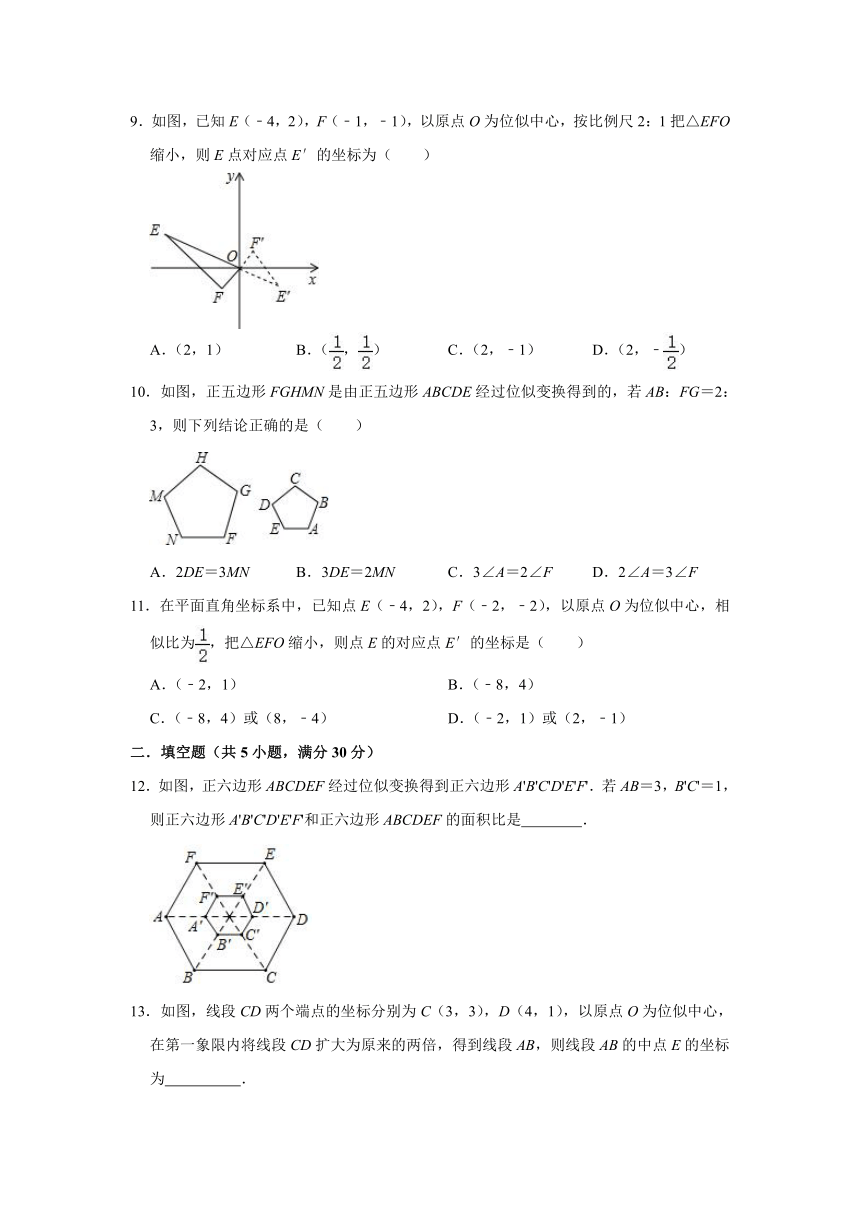
6.如图,△ABC与△DEF是位似图形,点O是位似中心,且△ABC的面积为4.若OA:OD=1:3,则△DEF的面积为( )
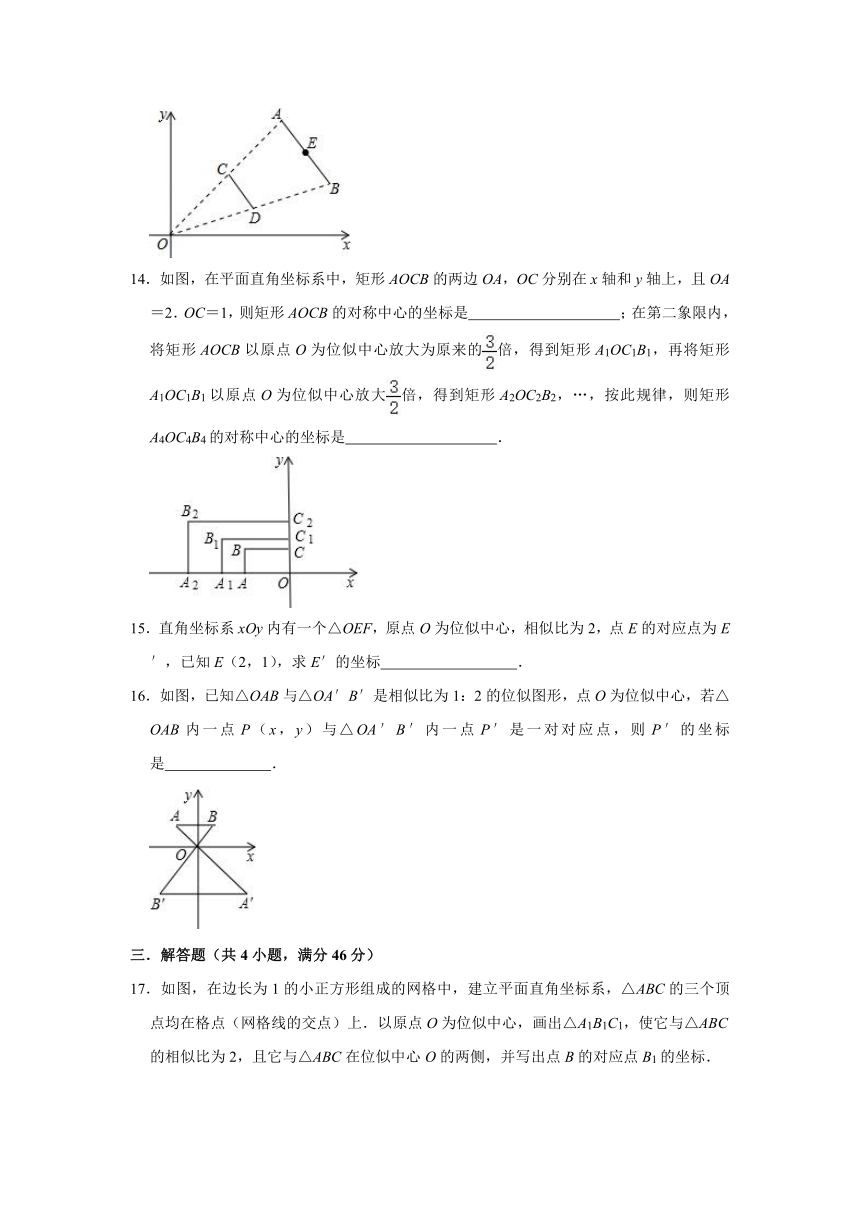
A.8 B.12 C.20 D.36
7.如图,在平面直角坐标系中,已知点A(﹣2,1),B(﹣1,2),以原点O为位似中心,相似比为2,把△ABO放大,则点B的对应点B′的坐标是( )
A.(﹣4,2) B.(﹣2,4)
C.(﹣4,2)或(﹣2,4) D.(﹣2,4)或(2,﹣4)
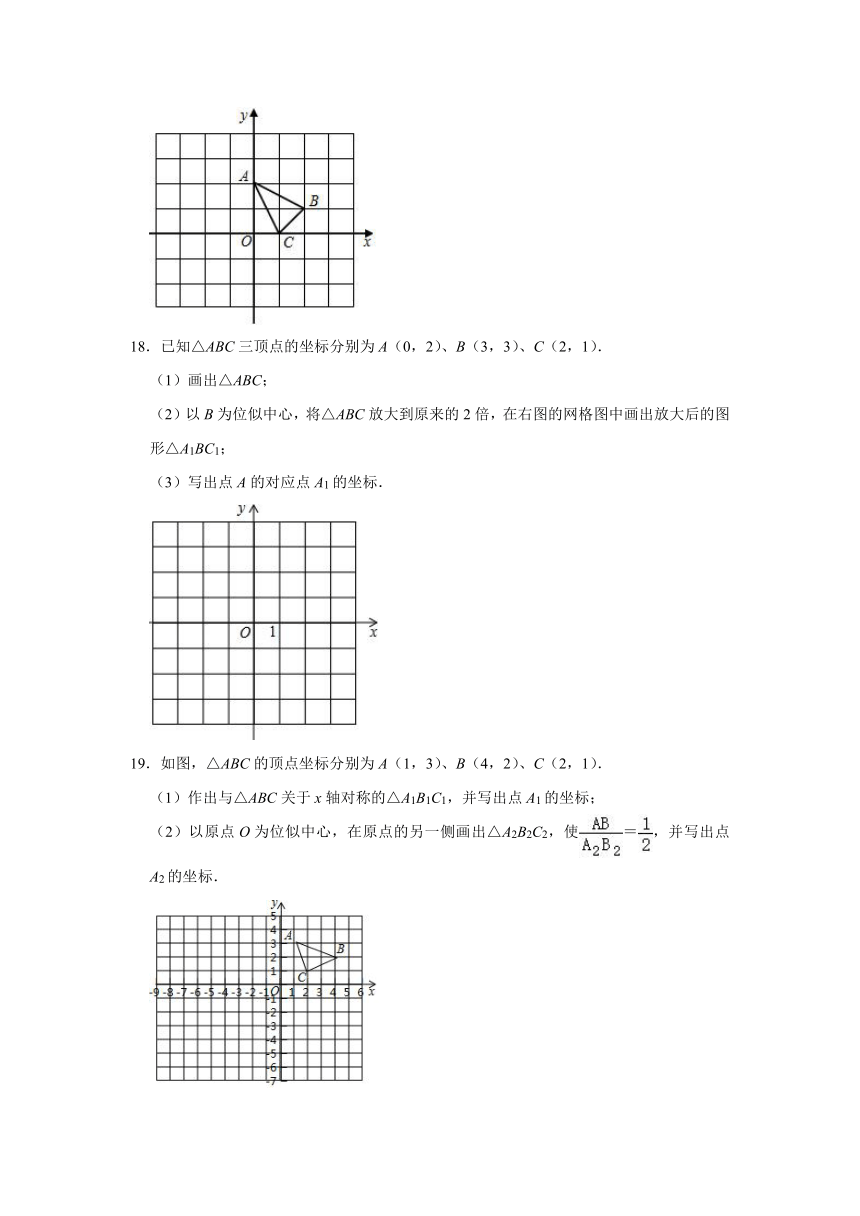
8.如图,△ABC与△A1B1C1是以O为位似中心的位似图形,若OA=3AA1,S△ABC=36,则S=( )
A.64 B.68 C.81 D.92
9.如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )
A.(2,1) B.(,) C.(2,﹣1) D.(2,﹣)
10.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
11.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
二.填空题(共5小题,满分30分)
12.如图,正六边形ABCDEF经过位似变换得到正六边形A'B'C'D'E'F'.若AB=3,B'C'=1,则正六边形A'B'C'D'E'F'和正六边形ABCDEF的面积比是 .
13.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为 .
14.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .
15.直角坐标系xOy内有一个△OEF,原点O为位似中心,相似比为2,点E的对应点为E′,已知E(2,1),求E′的坐标 .
16.如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则P′的坐标是 .
三.解答题(共4小题,满分46分)
17.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画出△A1B1C1,使它与△ABC的相似比为2,且它与△ABC在位似中心O的两侧,并写出点B的对应点B1的坐标.
18.已知△ABC三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).
(1)画出△ABC;
(2)以B为位似中心,将△ABC放大到原来的2倍,在右图的网格图中画出放大后的图形△A1BC1;
(3)写出点A的对应点A1的坐标.
19.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
20.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
参考答案
一.选择题(共11小题,满分44分)
1.解:设点C的坐标为(x,y),
∵△ABE和△CDE是以点E为位似中心的位似图形,
∴=,=,
解得,x=3,y=4,
则点C的坐标为(3,4),
故选:D.
2.解:A、位似中心要么取在图形外部,要么取在图形内部,也可以在图形上,故此选项错误;
B、位似中心取在图形内部时,也可以把图形缩小也可以放大,故此选项错误;
C、当位似中心确定后,按要求放大或缩小的图形能画2个,故此选项错误;
D、以上说法都不正确,符合题意.
故选:D.
3.解:∵正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,正方形BEFG的边长为12,
∴BC∥EF,=,BC=4,
∴△OBC∽△OEF,
∴==,即=,
解得,OB=6,
∴点C的坐标为(6,4),
故选:B.
4.解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
故选:D.
5.解:第一个图形中的位似中心为A点,第二个图形中的位似中心为BC的中点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.
故选:A.
6.解:∵△ABC与△DEF是位似图形,
∴△ABC∽△DEF,AC∥DF,
∴△OAC∽△ODF,
∴==,
∴=()2=,
∵△ABC的面积为4,
∴△DEF的面积为4×9=36,
故选:D.
7.解:∵以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,点B(﹣1,2),
∴B′点的坐标为(﹣2,4)或(2,﹣4).
故选:D.
8.解:∵△ABC与△A1B1C1是以O为位似中心的位似图形,
∴△ABC∽△A1B1C1,
∵OA=3AA1,
∴△ABC与△A1B1C1的相似比为:=,
∴△ABC与△A1B1C1的面积比为:()2=,
∵S△ABC=36,
∴S=36÷=64,
故选:A.
9.解:根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以﹣,
所以点E′的坐标为(2,﹣1).
故选:C.
10.解:∵正五边形FGHMN和正五边形ABCDE位似,
∴DE:MN=AB:FG=2:3,
∴3DE=2MN.
故选:B.
11.解:∵点E(﹣4,2),以O为位似中心,相似比为,
∴点E的对应点E′的坐标为:(﹣4×,2×)或(﹣4×(﹣),2×(﹣)),
即(﹣2,1)或(2,﹣1),
故选:D.
二.填空题(共5小题,满分30分)
12.解:∵正六边形ABCDEF是由正六边形A′B′C′D′E′F′经过位似变换得到的,
∴正六边形ABCDEF∽正六边形A′B′C′D′E′F′,
∴正六边形A′B′C′D′E′F′和正六边形ABCDEF的面积比=()2=1:9.
故答案为:1:9.
13.解:∵C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,
∴A(6,6),B(8,2),
∵E是AB中点,
∴E(7,4),
故答案为:(7,4).
14.解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
15.解:∵原点O为位似中心,相似比为2,E(2,1),
∴E′的坐标为(2×2,1×2)或[2×(﹣2),1×(﹣2)],即(4,2)或(﹣4,﹣2),
故答案为:(4,2)或(﹣4,﹣2).
16.解:∵P(x,y),相似比为1:2,点O为位似中心,
∴P′的坐标是(﹣2x,﹣2y).
三.解答题(共4小题,满分46分)
17.解:如图所示:点B的对应点B1的坐标是(﹣4,﹣2).
故答案为:(﹣4,﹣2).
18.解:(1)根据A(0,2)、B(3,3)、C(2,1).
在坐标系中找出连接即可;
(2)把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形.
所画图形如下所示:
它的三个对应顶点的坐标分别是:(﹣3,1)、(3,3)、(1,﹣1).
(3)利用(2)中图象,直接得出答案.
故答案为:(﹣3,1).
19.解:(1)如图,△A 1B1C1为所作,A1(1,﹣3);
(2)如图,△A2B2C2为所作,A2(﹣2,﹣6).
20.解:(1)如图所示:画出对称轴MN;
(2)对应边的比为1:2;
(3)图形A2B2C2D2的面积=×B2D2×A2C2=×4×8=16
一.选择题(共11小题,满分44分)
1.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
2.用位似方法把图形扩大或缩小时,下列说法中,正确的是( )
A.位似中心要么取在图形外部,要么取在图形内部
B.位似中心取在图形内部时,只能把图形缩小
C.当位似中心确定后,按要求放大或缩小的图形只能画一个
D.以上说法都不正确
3.如图,在平面直角坐标系xOy中,正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,点A,B,E在x轴上,若正方形BEFG的边长为12,则点C的坐标为( )
A.(6,2) B.(6,4) C.(4,4) D.(8,4)
4.如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
5.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是( )
A.4 B.3 C.2 D.1
6.如图,△ABC与△DEF是位似图形,点O是位似中心,且△ABC的面积为4.若OA:OD=1:3,则△DEF的面积为( )
A.8 B.12 C.20 D.36
7.如图,在平面直角坐标系中,已知点A(﹣2,1),B(﹣1,2),以原点O为位似中心,相似比为2,把△ABO放大,则点B的对应点B′的坐标是( )
A.(﹣4,2) B.(﹣2,4)
C.(﹣4,2)或(﹣2,4) D.(﹣2,4)或(2,﹣4)
8.如图,△ABC与△A1B1C1是以O为位似中心的位似图形,若OA=3AA1,S△ABC=36,则S=( )
A.64 B.68 C.81 D.92
9.如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )
A.(2,1) B.(,) C.(2,﹣1) D.(2,﹣)
10.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
11.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
二.填空题(共5小题,满分30分)
12.如图,正六边形ABCDEF经过位似变换得到正六边形A'B'C'D'E'F'.若AB=3,B'C'=1,则正六边形A'B'C'D'E'F'和正六边形ABCDEF的面积比是 .
13.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为 .
14.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .
15.直角坐标系xOy内有一个△OEF,原点O为位似中心,相似比为2,点E的对应点为E′,已知E(2,1),求E′的坐标 .
16.如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则P′的坐标是 .
三.解答题(共4小题,满分46分)
17.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画出△A1B1C1,使它与△ABC的相似比为2,且它与△ABC在位似中心O的两侧,并写出点B的对应点B1的坐标.
18.已知△ABC三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).
(1)画出△ABC;
(2)以B为位似中心,将△ABC放大到原来的2倍,在右图的网格图中画出放大后的图形△A1BC1;
(3)写出点A的对应点A1的坐标.
19.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
20.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
参考答案
一.选择题(共11小题,满分44分)
1.解:设点C的坐标为(x,y),
∵△ABE和△CDE是以点E为位似中心的位似图形,
∴=,=,
解得,x=3,y=4,
则点C的坐标为(3,4),
故选:D.
2.解:A、位似中心要么取在图形外部,要么取在图形内部,也可以在图形上,故此选项错误;
B、位似中心取在图形内部时,也可以把图形缩小也可以放大,故此选项错误;
C、当位似中心确定后,按要求放大或缩小的图形能画2个,故此选项错误;
D、以上说法都不正确,符合题意.
故选:D.
3.解:∵正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,正方形BEFG的边长为12,
∴BC∥EF,=,BC=4,
∴△OBC∽△OEF,
∴==,即=,
解得,OB=6,
∴点C的坐标为(6,4),
故选:B.
4.解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
故选:D.
5.解:第一个图形中的位似中心为A点,第二个图形中的位似中心为BC的中点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.
故选:A.
6.解:∵△ABC与△DEF是位似图形,
∴△ABC∽△DEF,AC∥DF,
∴△OAC∽△ODF,
∴==,
∴=()2=,
∵△ABC的面积为4,
∴△DEF的面积为4×9=36,
故选:D.
7.解:∵以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,点B(﹣1,2),
∴B′点的坐标为(﹣2,4)或(2,﹣4).
故选:D.
8.解:∵△ABC与△A1B1C1是以O为位似中心的位似图形,
∴△ABC∽△A1B1C1,
∵OA=3AA1,
∴△ABC与△A1B1C1的相似比为:=,
∴△ABC与△A1B1C1的面积比为:()2=,
∵S△ABC=36,
∴S=36÷=64,
故选:A.
9.解:根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以﹣,
所以点E′的坐标为(2,﹣1).
故选:C.
10.解:∵正五边形FGHMN和正五边形ABCDE位似,
∴DE:MN=AB:FG=2:3,
∴3DE=2MN.
故选:B.
11.解:∵点E(﹣4,2),以O为位似中心,相似比为,
∴点E的对应点E′的坐标为:(﹣4×,2×)或(﹣4×(﹣),2×(﹣)),
即(﹣2,1)或(2,﹣1),
故选:D.
二.填空题(共5小题,满分30分)
12.解:∵正六边形ABCDEF是由正六边形A′B′C′D′E′F′经过位似变换得到的,
∴正六边形ABCDEF∽正六边形A′B′C′D′E′F′,
∴正六边形A′B′C′D′E′F′和正六边形ABCDEF的面积比=()2=1:9.
故答案为:1:9.
13.解:∵C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,
∴A(6,6),B(8,2),
∵E是AB中点,
∴E(7,4),
故答案为:(7,4).
14.解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
15.解:∵原点O为位似中心,相似比为2,E(2,1),
∴E′的坐标为(2×2,1×2)或[2×(﹣2),1×(﹣2)],即(4,2)或(﹣4,﹣2),
故答案为:(4,2)或(﹣4,﹣2).
16.解:∵P(x,y),相似比为1:2,点O为位似中心,
∴P′的坐标是(﹣2x,﹣2y).
三.解答题(共4小题,满分46分)
17.解:如图所示:点B的对应点B1的坐标是(﹣4,﹣2).
故答案为:(﹣4,﹣2).
18.解:(1)根据A(0,2)、B(3,3)、C(2,1).
在坐标系中找出连接即可;
(2)把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形.
所画图形如下所示:
它的三个对应顶点的坐标分别是:(﹣3,1)、(3,3)、(1,﹣1).
(3)利用(2)中图象,直接得出答案.
故答案为:(﹣3,1).
19.解:(1)如图,△A 1B1C1为所作,A1(1,﹣3);
(2)如图,△A2B2C2为所作,A2(﹣2,﹣6).
20.解:(1)如图所示:画出对称轴MN;
(2)对应边的比为1:2;
(3)图形A2B2C2D2的面积=×B2D2×A2C2=×4×8=16
同课章节目录
