2021-2022学年浙教版九年级数学上册4.5相似三角形的性质及应用同步测评(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册4.5相似三角形的性质及应用同步测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 295.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 23:10:59 | ||
图片预览



文档简介
2021-2022学年浙教版九年级数学上册《4.5相似三角形的性质及应用》同步测评(附答案)
一.选择题(共10小题,满分40分)
1.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( )
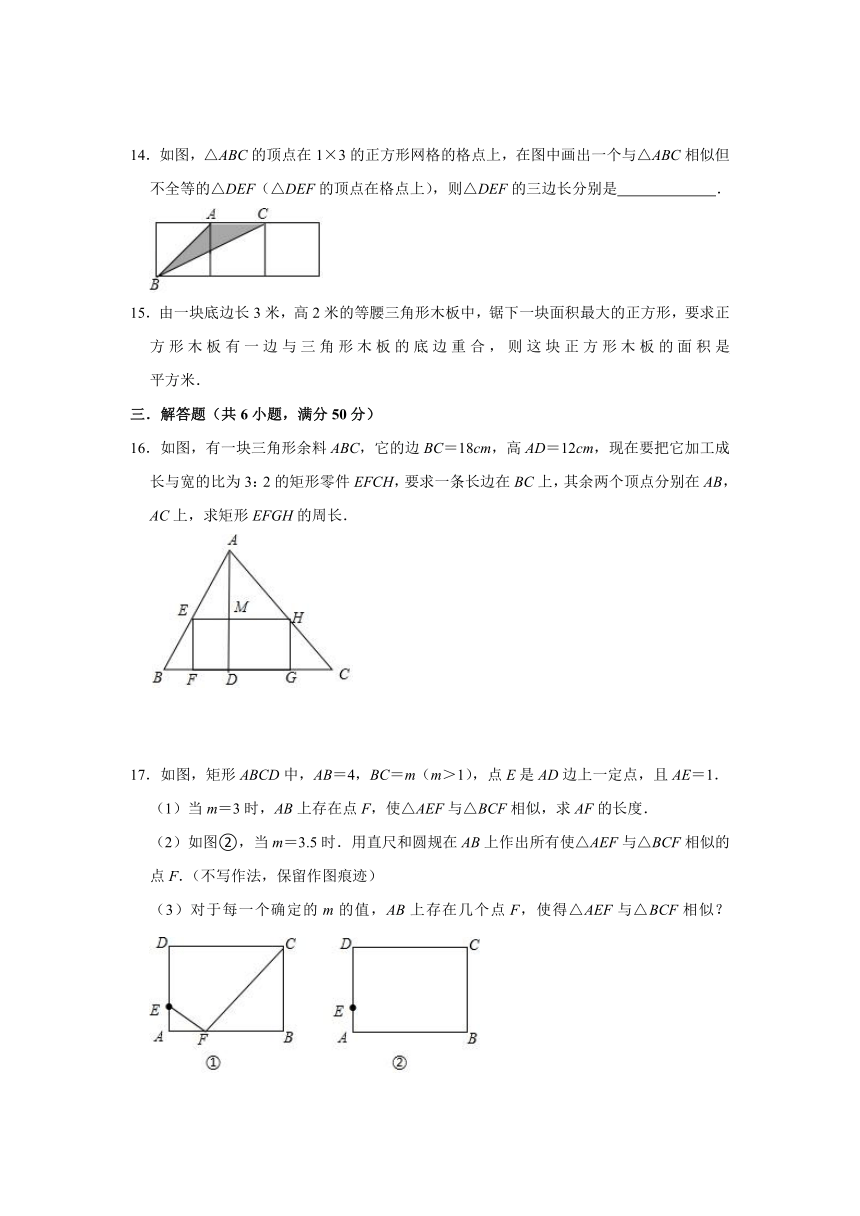
A.8米 B.14.4米 C.16米 D.20米
2.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A.3 B.9 C.12 D.24
3.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
4.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
5.小宸同学的身高为1.8m,测得他站立在阳光下的影长为0.9m,紧接着他把手臂竖直举起,测得影长为1.2m,那么小宸举起的手臂超出头顶的高度为( )
A.0.3m B.0.5m C.0.6m D.2.1m
6.某一时刻,一根4米长的旗杆的影子长6米,同一时刻一座建筑物的影子长36米,则这座建筑物的高度为( )米.
A.22 B.20 C.26 D.24
7.一个钢筋三角架三边长分别为20cm,50cm,60cm,现在要做一个和它相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种
C.三种 D.四种或四种以上
8.现有一张Rt△ABC纸片,直角边BC长为l2cm,另一直角边AB长为24cm.现沿BC边依次从下往上裁剪宽度均为3cm的矩形纸条,如图.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
9.如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
10.王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )
A.1:14 B.3:14 C.1:16 D.3:16
二.填空题(共5小题,满分30分)
11.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
12.如图,一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2.按图中要求加工成一个正方形桌面,则桌面的边长为 m.
13.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
14.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
15.由一块底边长3米,高2米的等腰三角形木板中,锯下一块面积最大的正方形,要求正方形木板有一边与三角形木板的底边重合,则这块正方形木板的面积是 平方米.
三.解答题(共6小题,满分50分)
16.如图,有一块三角形余料ABC,它的边BC=18cm,高AD=12cm,现在要把它加工成长与宽的比为3:2的矩形零件EFCH,要求一条长边在BC上,其余两个顶点分别在AB,AC上,求矩形EFGH的周长.
17.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
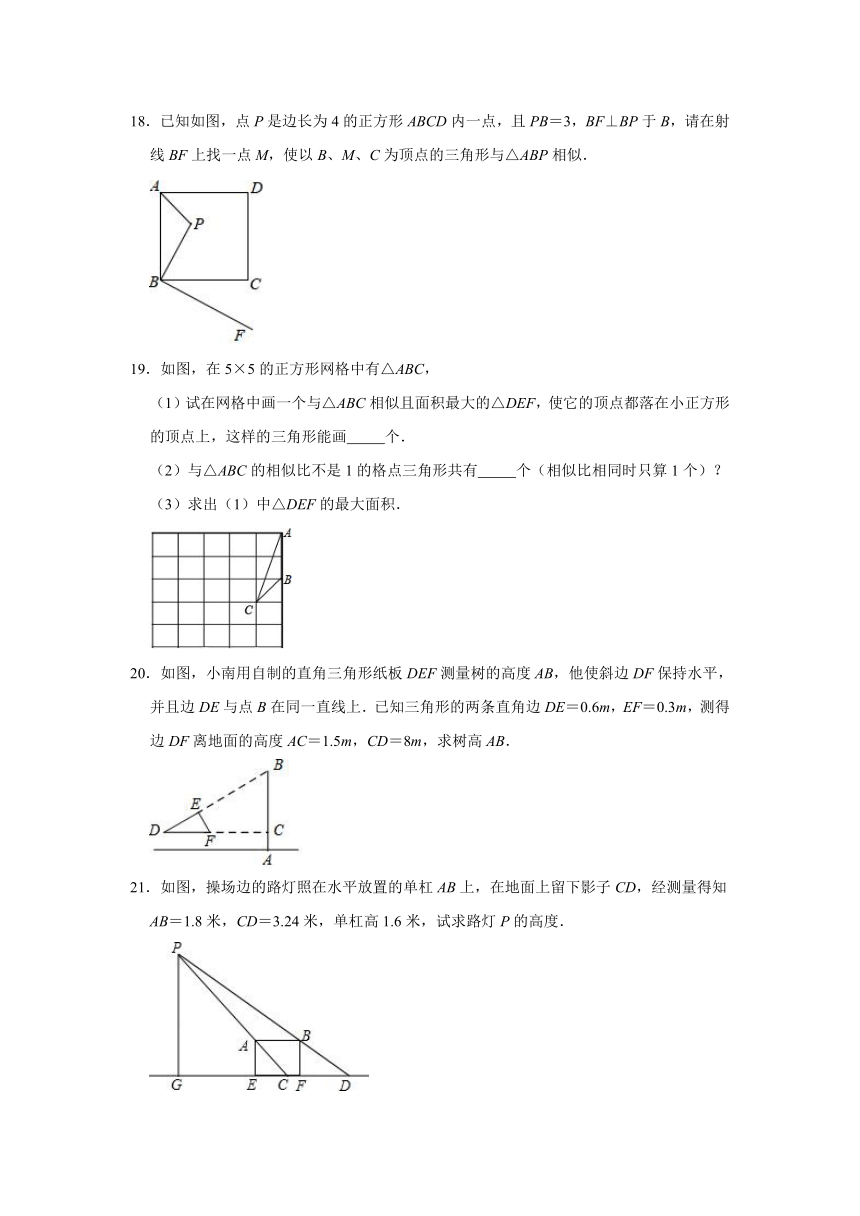
18.已知如图,点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP于B,请在射线BF上找一点M,使以B、M、C为顶点的三角形与△ABP相似.
19.如图,在5×5的正方形网格中有△ABC,
(1)试在网格中画一个与△ABC相似且面积最大的△DEF,使它的顶点都落在小正方形的顶点上,这样的三角形能画 个.
(2)与△ABC的相似比不是1的格点三角形共有 个(相似比相同时只算1个)?
(3)求出(1)中△DEF的最大面积.
20.如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.已知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
21.如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.
参考答案
一.选择题(共10小题,满分40分)
1.解:设旗杆高度为h,
由题意得=,
解得:h=16米.
故选:C.
2.解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
故选:C.
3.解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则=,
∵AO=4m,AB=1.6m,CO=1m,
∴=,
解得:CD=0.4m,
故选:C.
4.解:∵DE∥BC,
∴△AED∽△ACB
∴,
设屏幕上的小树高是x,则,
解得x=18cm.
故选:C.
5.解:设手臂竖直举起时总高度xm,列方程得:=,
解得x=2.4,
2.4﹣1.8=0.6m,
所以小刚举起的手臂超出头顶的高度为0.6m.
故选:C.
6.解:设建筑物高为x,根据在同一时刻同一地点任何物体的高与其影子长的比值相同得=,
∴x=24,
∴建筑物的高为24米,
故选:D.
7.解:由相似三角形对应边成比例可知,只能将30cm长的作为一边,将50cm长的截成两段,
设从50cm的钢筋上截下的两段分别长xcm,ycm,
当30cm长的边对应20cm长的边时,,x=75(cm),x>50(cm),不成立;
当30cm长的边对应50cm长的边时,,x=12(cm),y=36(cm),x+y=48cm<50cm,成立;
当30cm长的边对应60cm长的边时,,x=10(cm),y=25(cm),x+y=35cm<50cm,成立.
故选:B.
8.解:设这张正方形纸条是第n张.
∵EF∥BC,
∴△AEF∽△ABC,
∴,
解得:n=6.
故选:C.
9.解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则,解得x=3,
所以另一段长为18﹣3=15,
因为15÷3=5,所以是第5张.
故选:B.
10.解:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD=3,BC=9,
即AD:BC=1:3,
∴△AOD与△BOC的面积比等于:1:9.
∵△ADO与△ABO等高,
∴S△ADO:S△ABO=OD:OB=AD:BC=1:3,
同理可得:S△ADO:S△DCO=OA:OC=AD:BC=1:3
∴王大爷种大白菜的面积与整个土地的面积比为1:16
故选:C.
二.填空题(共5小题,满分30分)
11.解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
12.解:∵一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2,
∴另一直角边长为:=2(m),
则斜边长为:=2.5,
设点C到AB的距离为h,
则S△ABC=×2.5h=1.5,
解得:h=1.2,
∵正方形GFDE的边DE∥GF,
∴△ACB∽△DCE,
=,
即=,
解得:x=,
故答案为:.
13.解:DH=100,DK=100,AH=15,
∵AH∥DK,
∴∠CDK=∠A,
而∠CKD=∠AHD,
∴△CDK∽△DAH,
∴=,即=,
∴CK=.
答:KC的长为步.
故答案为.
14.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
15.解:设正方形的边长为xm,
∵底长3m、高2m,
∴=,
解得:x=,
∴正方形的面积为:m2.
故答案为:.
三.解答题(共6小题,满分50分)
16.解:∵矩形EFGH中,EH∥FG,EH=GF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AM⊥EH,
∴=,
设EH=3x,则MD=EF=2x,AM=12﹣2x,
∴=,
解得:x=3,
∴EH=3x=9,EF=2x=6,
∴矩形EFGH的周长为:2×(9+6)=30(cm).
17.解:(1)当∠AEF=∠BFC时,
要使△AEF∽△BFC,需=,即=,
解得AF=1或3;
当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即=,
解得AF=1;
综上所述AF=1或3.
(2)延长DA,作点E关于AB的对称点E′,连接CE′,交AB于点F1;
连接CE,以CE为直径作圆交AB于点F2、F3.
(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;
当m=4时,有2个;
当m>4时,有1个.
18.解:∵四边形ABCD为正方形,PB⊥BF,
∴∠ABC=∠PBF=90°,
∴∠ABP+∠PBC=∠PBC+∠CBF,
∴∠ABP=∠CBF,
当△ABP∽△CBM时,则有=,即=,
解得BM=3;
当△ABP∽△MBC时,则有=,即=,
解得BM=;
∴BM=3或.
19.解:(1)在图中所给的网格中共能画出8个与△ABC相似且面积最大的格点三角形;
(2)与△ABC的相似比不是1的格点三角形共有4个;
(3)△DEF就是所求的最大的相似三角形.
S△ABC==1
根据相似三角形面积比等于相似比的平方可得S△DEF=5
故答案为:(1)8;(2)4.
20.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB
∴=,
∵DE=0.6m,EF=0.3m,AC=1.5m,CD=8m,
∴=,
∴BC=4米,
∴AB=AC+BC=1.5+5=5.5米.
答:树高5.5米.
21.解:∵AB∥CD,
∴△PAB∽△PCD,
∴===,
∴=,
∵AE∥PG,
∴△CAE∽△CPG,
∴=,即=,
∴PG=3.6(m).
答:路灯P的高度为3.6m.
一.选择题(共10小题,满分40分)
1.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( )
A.8米 B.14.4米 C.16米 D.20米
2.如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A.3 B.9 C.12 D.24
3.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
4.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
5.小宸同学的身高为1.8m,测得他站立在阳光下的影长为0.9m,紧接着他把手臂竖直举起,测得影长为1.2m,那么小宸举起的手臂超出头顶的高度为( )
A.0.3m B.0.5m C.0.6m D.2.1m
6.某一时刻,一根4米长的旗杆的影子长6米,同一时刻一座建筑物的影子长36米,则这座建筑物的高度为( )米.
A.22 B.20 C.26 D.24
7.一个钢筋三角架三边长分别为20cm,50cm,60cm,现在要做一个和它相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种
C.三种 D.四种或四种以上
8.现有一张Rt△ABC纸片,直角边BC长为l2cm,另一直角边AB长为24cm.现沿BC边依次从下往上裁剪宽度均为3cm的矩形纸条,如图.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
9.如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
10.王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )
A.1:14 B.3:14 C.1:16 D.3:16
二.填空题(共5小题,满分30分)
11.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为 步.
12.如图,一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2.按图中要求加工成一个正方形桌面,则桌面的边长为 m.
13.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为 步.
14.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
15.由一块底边长3米,高2米的等腰三角形木板中,锯下一块面积最大的正方形,要求正方形木板有一边与三角形木板的底边重合,则这块正方形木板的面积是 平方米.
三.解答题(共6小题,满分50分)
16.如图,有一块三角形余料ABC,它的边BC=18cm,高AD=12cm,现在要把它加工成长与宽的比为3:2的矩形零件EFCH,要求一条长边在BC上,其余两个顶点分别在AB,AC上,求矩形EFGH的周长.
17.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
18.已知如图,点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP于B,请在射线BF上找一点M,使以B、M、C为顶点的三角形与△ABP相似.
19.如图,在5×5的正方形网格中有△ABC,
(1)试在网格中画一个与△ABC相似且面积最大的△DEF,使它的顶点都落在小正方形的顶点上,这样的三角形能画 个.
(2)与△ABC的相似比不是1的格点三角形共有 个(相似比相同时只算1个)?
(3)求出(1)中△DEF的最大面积.
20.如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.已知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
21.如图,操场边的路灯照在水平放置的单杠AB上,在地面上留下影子CD,经测量得知AB=1.8米,CD=3.24米,单杠高1.6米,试求路灯P的高度.
参考答案
一.选择题(共10小题,满分40分)
1.解:设旗杆高度为h,
由题意得=,
解得:h=16米.
故选:C.
2.解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴=,
∵MB=6,BE=4,
∴===,
∵AB=BC,
∴=,
设CE=2x,则BC=3x,在Rt△CBE中,
BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=,
∴CE=,AB=BC=,AM=AB=,
∴S草皮=S△CBE+S△AMB=××+××
=12.
故选:C.
3.解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则=,
∵AO=4m,AB=1.6m,CO=1m,
∴=,
解得:CD=0.4m,
故选:C.
4.解:∵DE∥BC,
∴△AED∽△ACB
∴,
设屏幕上的小树高是x,则,
解得x=18cm.
故选:C.
5.解:设手臂竖直举起时总高度xm,列方程得:=,
解得x=2.4,
2.4﹣1.8=0.6m,
所以小刚举起的手臂超出头顶的高度为0.6m.
故选:C.
6.解:设建筑物高为x,根据在同一时刻同一地点任何物体的高与其影子长的比值相同得=,
∴x=24,
∴建筑物的高为24米,
故选:D.
7.解:由相似三角形对应边成比例可知,只能将30cm长的作为一边,将50cm长的截成两段,
设从50cm的钢筋上截下的两段分别长xcm,ycm,
当30cm长的边对应20cm长的边时,,x=75(cm),x>50(cm),不成立;
当30cm长的边对应50cm长的边时,,x=12(cm),y=36(cm),x+y=48cm<50cm,成立;
当30cm长的边对应60cm长的边时,,x=10(cm),y=25(cm),x+y=35cm<50cm,成立.
故选:B.
8.解:设这张正方形纸条是第n张.
∵EF∥BC,
∴△AEF∽△ABC,
∴,
解得:n=6.
故选:C.
9.解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则,解得x=3,
所以另一段长为18﹣3=15,
因为15÷3=5,所以是第5张.
故选:B.
10.解:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD=3,BC=9,
即AD:BC=1:3,
∴△AOD与△BOC的面积比等于:1:9.
∵△ADO与△ABO等高,
∴S△ADO:S△ABO=OD:OB=AD:BC=1:3,
同理可得:S△ADO:S△DCO=OA:OC=AD:BC=1:3
∴王大爷种大白菜的面积与整个土地的面积比为1:16
故选:C.
二.填空题(共5小题,满分30分)
11.解:设正方形城池的边长为x步,则AE=CE=x,
∵AE∥CD,
∴∠BEA=∠EDC,
∴Rt△BEA∽Rt△EDC,
∴=,即=,
∴x=300,
即正方形城池的边长为300步.
故答案为300.
12.解:∵一块直角三角形木板,一条直角边AC的长1.5m,面积为1.5m2,
∴另一直角边长为:=2(m),
则斜边长为:=2.5,
设点C到AB的距离为h,
则S△ABC=×2.5h=1.5,
解得:h=1.2,
∵正方形GFDE的边DE∥GF,
∴△ACB∽△DCE,
=,
即=,
解得:x=,
故答案为:.
13.解:DH=100,DK=100,AH=15,
∵AH∥DK,
∴∠CDK=∠A,
而∠CKD=∠AHD,
∴△CDK∽△DAH,
∴=,即=,
∴CK=.
答:KC的长为步.
故答案为.
14.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
15.解:设正方形的边长为xm,
∵底长3m、高2m,
∴=,
解得:x=,
∴正方形的面积为:m2.
故答案为:.
三.解答题(共6小题,满分50分)
16.解:∵矩形EFGH中,EH∥FG,EH=GF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AM⊥EH,
∴=,
设EH=3x,则MD=EF=2x,AM=12﹣2x,
∴=,
解得:x=3,
∴EH=3x=9,EF=2x=6,
∴矩形EFGH的周长为:2×(9+6)=30(cm).
17.解:(1)当∠AEF=∠BFC时,
要使△AEF∽△BFC,需=,即=,
解得AF=1或3;
当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即=,
解得AF=1;
综上所述AF=1或3.
(2)延长DA,作点E关于AB的对称点E′,连接CE′,交AB于点F1;
连接CE,以CE为直径作圆交AB于点F2、F3.
(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;
当m=4时,有2个;
当m>4时,有1个.
18.解:∵四边形ABCD为正方形,PB⊥BF,
∴∠ABC=∠PBF=90°,
∴∠ABP+∠PBC=∠PBC+∠CBF,
∴∠ABP=∠CBF,
当△ABP∽△CBM时,则有=,即=,
解得BM=3;
当△ABP∽△MBC时,则有=,即=,
解得BM=;
∴BM=3或.
19.解:(1)在图中所给的网格中共能画出8个与△ABC相似且面积最大的格点三角形;
(2)与△ABC的相似比不是1的格点三角形共有4个;
(3)△DEF就是所求的最大的相似三角形.
S△ABC==1
根据相似三角形面积比等于相似比的平方可得S△DEF=5
故答案为:(1)8;(2)4.
20.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB
∴=,
∵DE=0.6m,EF=0.3m,AC=1.5m,CD=8m,
∴=,
∴BC=4米,
∴AB=AC+BC=1.5+5=5.5米.
答:树高5.5米.
21.解:∵AB∥CD,
∴△PAB∽△PCD,
∴===,
∴=,
∵AE∥PG,
∴△CAE∽△CPG,
∴=,即=,
∴PG=3.6(m).
答:路灯P的高度为3.6m.
同课章节目录
