4.2.1平面直角坐标系及其相关的概念 课件(共22张PPT)
文档属性
| 名称 | 4.2.1平面直角坐标系及其相关的概念 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
4.2.1探索确定位置的方法
浙教版 八年级上
新知导入
如图: 是某市旅游景点示意图,如果把 “玉泉”的位置作为起点.
用有序数对表
“镇海楼”的位置;
“鼓楼”的位置;
“龙珠湖”的位置.
鼓楼
北
人民广场
会展中心
龙珠湖
玉泉
灵石塔
镇海楼
(7,3)
(1,3)
(8,0)
新知导入
笛卡尔(1596-1660) ,法国数学家、科学家和哲学家。
早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
知识讲解
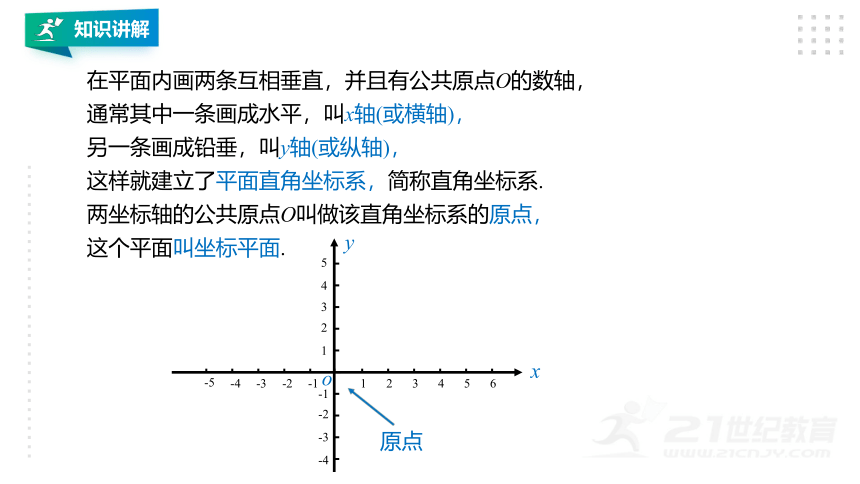
在平面内画两条互相垂直,并且有公共原点O的数轴,
通常其中一条画成水平,叫x轴(或横轴),
另一条画成铅垂,叫y轴(或纵轴),
这样就建立了平面直角坐标系,简称直角坐标系.
两坐标轴的公共原点O叫做该直角坐标系的原点,
这个平面叫坐标平面.
y
1
2
3
4
5
-1
-2
-3
-4
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
原点
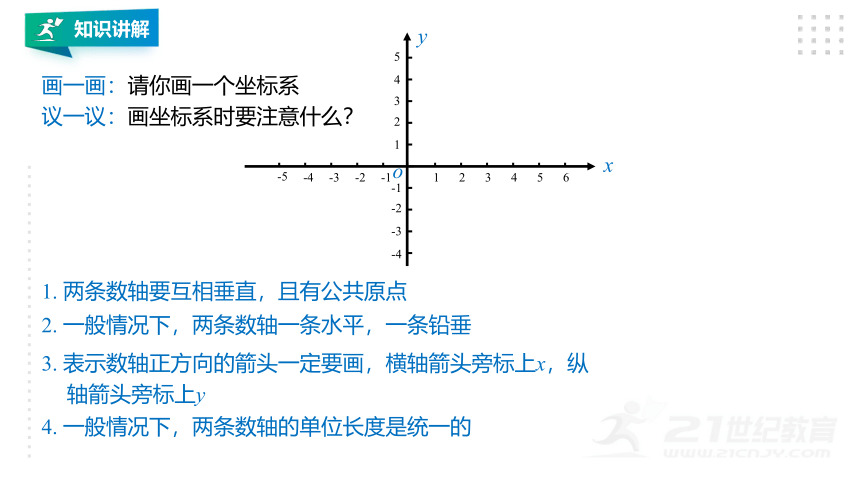
画一画:请你画一个坐标系
议一议:画坐标系时要注意什么?
1. 两条数轴要互相垂直,且有公共原点
2. 一般情况下,两条数轴一条水平,一条铅垂
4. 一般情况下,两条数轴的单位长度是统一的
3. 表示数轴正方向的箭头一定要画,横轴箭头旁标上x,纵轴箭头旁标上y
y
1
2
3
4
5
-1
-2
-3
-4
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
知识讲解
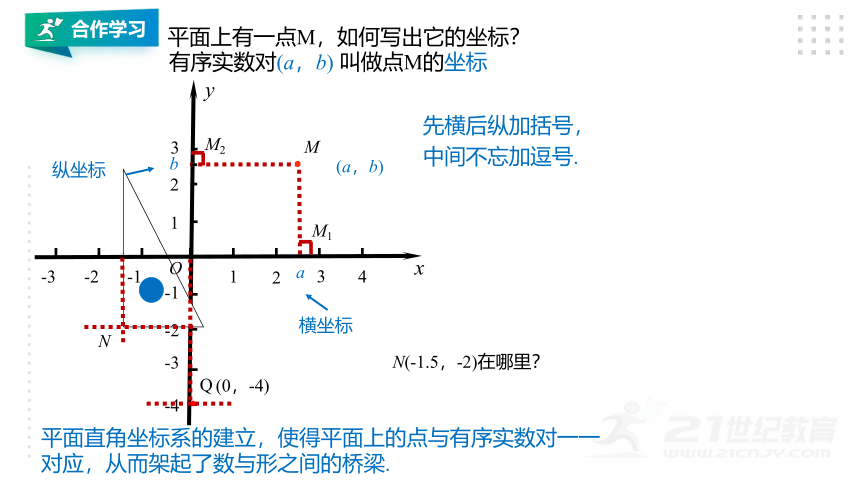
合作学面上有一点M,如何写出它的坐标?
有序实数对(a,b) 叫做点M的坐标
(a,b)
3
1
2
-2
-4
-1
-3
O
1
2
4
-3
-2
-1
M
.
x
a
b
M1
M2
·
Q
(0,-4)
y
先横后纵加括号,
中间不忘加逗号.
横坐标
纵坐标
N
N(-1.5,-2)在哪里?
平面直角坐标系的建立,使得平面上的点与有序实数对一一对应,从而架起了数与形之间的桥梁.
3
例题讲解
y
0 1 2 3 4 5 6
6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
x
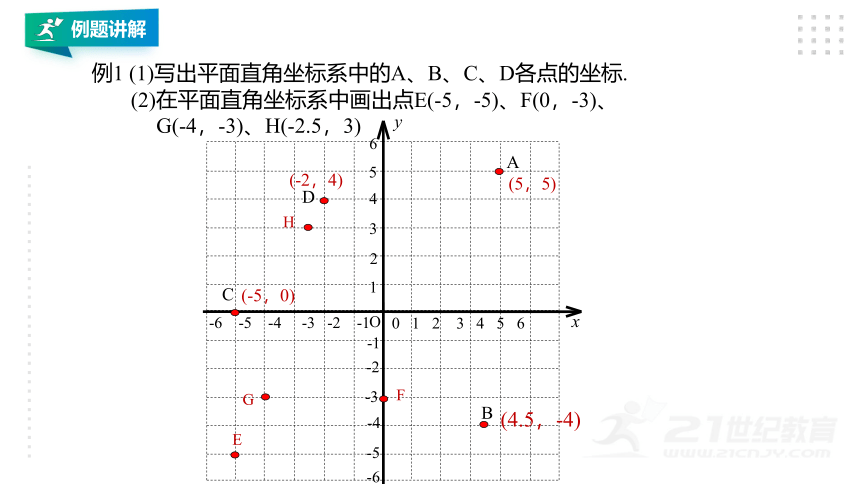
例1 (1)写出平面直角坐标系中的A、B、C、D各点的坐标.
A
H
E
B
G
C
F
(2)在平面直角坐标系中画出点E(-5,-5)、F(0,-3)、G(-4,-3)、H(-2.5,3)
(5,5)
(4.5,-4)
(-5,0)
(-2,4)
D
O
合作探究
O
第一象限
第二象限
第三象限
第四象限
x
y
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
4
4
-4
-4
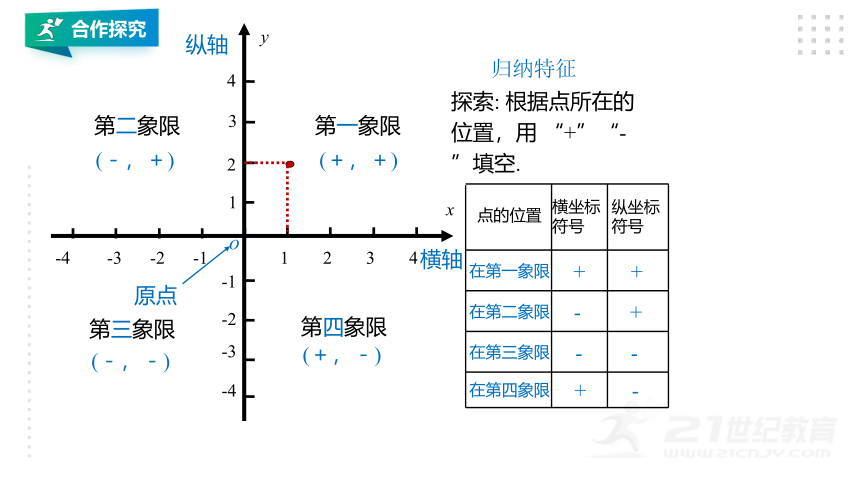
通过练习,我们来探究:在各个象限以及x轴、y轴上的点的坐标有什么特征?
(-,+)
(+,+)
(-,-)
(+,-)
x轴上的点的纵坐标为0,表示为(a,0)
y轴上的点的横坐标为0,表示为(0,b)
注意:坐标轴上的点不属于任何象限
横轴(x轴)与纵轴(y轴)将坐标平面分为
四部分
合作探究
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
(+,+)
(-,+)
(-,-)
(+,-)
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
+
+
+
-
-
+
-
-
纵坐标
符号
探索: 根据点所在的位置,用 “+”“-”填空.
-4
o
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
归纳特征
·
B
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
C
·
A
·
E
·
D
例2: 已知A、B、C、D、E在直角坐标系的位置如下,请你求出它们的坐标分别是多少?并表示出来?
(-2,1.5)
(2,3)
(3,2)
(1,-2)
(-4,-2.5)
例题讲解
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
·
·
·
B
C
A
D
在直角坐标系中,画出
下列各点:A(4,3),
B(-2,3),C(-4,-1),
D(2,-2)
思考:
每个象限上的数,它的坐标有什么特点
( +,+)
( -,+)
( - , - )
( +,-)
请问(2,5),(7,-4),(-14,9),(-5,-6)分别属于第几象限?
( 4,3 )
( -2,3)
( -4,- 1)
( 2,-2 )
课内练习
课堂小结
1、能够正确画出直角坐标系.
2、能在直角坐标系中,根据坐标找出点, 由点求出坐标.
第一象限(+,+) 第二象限(-,+)
第三象限(-,-) 第四象限(+,-)
4、掌握各个象限内点、x轴,y轴上点的坐标的特点.
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3、坐标平面内的点与有序实数对一一对应.
课内练习
(1)下列点中,位于第二象限的是( )
A.(2,-3) B.(-2,-3) C.(-2,3) D.(2,3)
(2)若点A(x,y)的坐标满足xy=0,则点A在( )上
A.原点 B.x轴 C.y轴 D.x轴或y轴
C
D
(3)横坐标为负,纵坐标为正的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
(4)已知点A(2,3), B(0,-2), C(3,0), D(-1,2),其中在第二象限内的点的个数是( )
A.0 B.1 C.2 D.3
B
1. 选择题
课内练习
(1)下列说法正确的有_______________
(1)直角坐标系中,点(3,0)在横轴上,点(0,-3)在纵轴上
(2)直角坐标系中,原点既在x轴上又在y轴上
(3)(2,-5)与(-5,2)表示两个不同的点
(4)仅有两条互相垂直的直线就可以组成平面直角坐标系
(1) (2) (3)
(2) 如点(2m,m-4)在第四象限,且m为偶数,则m= .
2
(3)若点A(2x-8,x-2)在第二象限,且x为整数,则点A的坐
标为 .
解析: 第二象限内点的横坐标小于0,纵坐标大于0,∴2又∵x为整数,∴x=3.
∴点A的坐标为(-2,1).
(-2,1)
2. 填空题
课内练习
3.(1)如图,写出A,B, C,D,E,O各点的坐标.
(2)在直角坐标系中描出点M(2,4),N(-2,1) ,P(0,-4),
Q(4,-3).
解: (1)点A(2,1),B(-3,5),C(-4,0),
D(0,3),E(-3,-2),O(0,0).
(2)∵点M(2,4),∴先在x轴上找到坐标为2的点,并过这个点画x轴的垂线,再在y轴上找到坐标为4的点,并过这个点作y轴的垂线,这两条垂线的交点就是点M,同理可描出点N,P,Q.
课内练习
4.(1)在平面直角坐标系中画出点M(5,3)、A ,
C(-4.5,0)、D(0,-4)、H 、B(0,4) 、 E 、
F .
1 2 3 4 5 6
6
5
4
3
2
1
y
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
M(5,3)
D
C
B
E
F
课内练习
(2)请用彩色笔和直尺将其中七个点按照A→B→C→D→E→F→H→A的顺序依次连接起来;
(3)请为你的作品画出点睛之笔,并写出该点R的坐标.
-1
-2
-3
-4
-5
-6
1 2 3 4 5 6
4
3
2
1
y
-6 -5 -4 -3 -2 -1
x
B
E
F
A
C
D
R(-3,0)
H
5
6
O
课内练习
5.在平面直角坐标系中,若点P(m+2,m-3)在第四象限,求m的取值范围.
解析: 第四象限的点的横坐标为正,纵坐标为负.
解: ∵点P在第四象限,∴点P的横坐标为正,纵坐标为负,
∴
∴-2m+2>0
m-3<0
课内练习
6.请在平面直角坐标系中描出下列各点:A(-2,-4),
B(5,3),C(0,4),D(-3,5),并指出各点所在的象限或坐标轴.
解: 各点在坐标系中的位置如解图.点A在第三象限,
点B在第一象限,点C在y轴上,点D在第二象限.
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
4.2.1探索确定位置的方法
浙教版 八年级上
新知导入
如图: 是某市旅游景点示意图,如果把 “玉泉”的位置作为起点.
用有序数对表
“镇海楼”的位置;
“鼓楼”的位置;
“龙珠湖”的位置.
鼓楼
北
人民广场
会展中心
龙珠湖
玉泉
灵石塔
镇海楼
(7,3)
(1,3)
(8,0)
新知导入
笛卡尔(1596-1660) ,法国数学家、科学家和哲学家。
早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
知识讲解
在平面内画两条互相垂直,并且有公共原点O的数轴,
通常其中一条画成水平,叫x轴(或横轴),
另一条画成铅垂,叫y轴(或纵轴),
这样就建立了平面直角坐标系,简称直角坐标系.
两坐标轴的公共原点O叫做该直角坐标系的原点,
这个平面叫坐标平面.
y
1
2
3
4
5
-1
-2
-3
-4
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
原点
画一画:请你画一个坐标系
议一议:画坐标系时要注意什么?
1. 两条数轴要互相垂直,且有公共原点
2. 一般情况下,两条数轴一条水平,一条铅垂
4. 一般情况下,两条数轴的单位长度是统一的
3. 表示数轴正方向的箭头一定要画,横轴箭头旁标上x,纵轴箭头旁标上y
y
1
2
3
4
5
-1
-2
-3
-4
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
知识讲解
合作学面上有一点M,如何写出它的坐标?
有序实数对(a,b) 叫做点M的坐标
(a,b)
3
1
2
-2
-4
-1
-3
O
1
2
4
-3
-2
-1
M
.
x
a
b
M1
M2
·
Q
(0,-4)
y
先横后纵加括号,
中间不忘加逗号.
横坐标
纵坐标
N
N(-1.5,-2)在哪里?
平面直角坐标系的建立,使得平面上的点与有序实数对一一对应,从而架起了数与形之间的桥梁.
3
例题讲解
y
0 1 2 3 4 5 6
6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
x
例1 (1)写出平面直角坐标系中的A、B、C、D各点的坐标.
A
H
E
B
G
C
F
(2)在平面直角坐标系中画出点E(-5,-5)、F(0,-3)、G(-4,-3)、H(-2.5,3)
(5,5)
(4.5,-4)
(-5,0)
(-2,4)
D
O
合作探究
O
第一象限
第二象限
第三象限
第四象限
x
y
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
4
4
-4
-4
通过练习,我们来探究:在各个象限以及x轴、y轴上的点的坐标有什么特征?
(-,+)
(+,+)
(-,-)
(+,-)
x轴上的点的纵坐标为0,表示为(a,0)
y轴上的点的横坐标为0,表示为(0,b)
注意:坐标轴上的点不属于任何象限
横轴(x轴)与纵轴(y轴)将坐标平面分为
四部分
合作探究
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
(+,+)
(-,+)
(-,-)
(+,-)
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
+
+
+
-
-
+
-
-
纵坐标
符号
探索: 根据点所在的位置,用 “+”“-”填空.
-4
o
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
归纳特征
·
B
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
C
·
A
·
E
·
D
例2: 已知A、B、C、D、E在直角坐标系的位置如下,请你求出它们的坐标分别是多少?并表示出来?
(-2,1.5)
(2,3)
(3,2)
(1,-2)
(-4,-2.5)
例题讲解
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
·
·
·
B
C
A
D
在直角坐标系中,画出
下列各点:A(4,3),
B(-2,3),C(-4,-1),
D(2,-2)
思考:
每个象限上的数,它的坐标有什么特点
( +,+)
( -,+)
( - , - )
( +,-)
请问(2,5),(7,-4),(-14,9),(-5,-6)分别属于第几象限?
( 4,3 )
( -2,3)
( -4,- 1)
( 2,-2 )
课内练习
课堂小结
1、能够正确画出直角坐标系.
2、能在直角坐标系中,根据坐标找出点, 由点求出坐标.
第一象限(+,+) 第二象限(-,+)
第三象限(-,-) 第四象限(+,-)
4、掌握各个象限内点、x轴,y轴上点的坐标的特点.
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3、坐标平面内的点与有序实数对一一对应.
课内练习
(1)下列点中,位于第二象限的是( )
A.(2,-3) B.(-2,-3) C.(-2,3) D.(2,3)
(2)若点A(x,y)的坐标满足xy=0,则点A在( )上
A.原点 B.x轴 C.y轴 D.x轴或y轴
C
D
(3)横坐标为负,纵坐标为正的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
(4)已知点A(2,3), B(0,-2), C(3,0), D(-1,2),其中在第二象限内的点的个数是( )
A.0 B.1 C.2 D.3
B
1. 选择题
课内练习
(1)下列说法正确的有_______________
(1)直角坐标系中,点(3,0)在横轴上,点(0,-3)在纵轴上
(2)直角坐标系中,原点既在x轴上又在y轴上
(3)(2,-5)与(-5,2)表示两个不同的点
(4)仅有两条互相垂直的直线就可以组成平面直角坐标系
(1) (2) (3)
(2) 如点(2m,m-4)在第四象限,且m为偶数,则m= .
2
(3)若点A(2x-8,x-2)在第二象限,且x为整数,则点A的坐
标为 .
解析: 第二象限内点的横坐标小于0,纵坐标大于0,∴2
∴点A的坐标为(-2,1).
(-2,1)
2. 填空题
课内练习
3.(1)如图,写出A,B, C,D,E,O各点的坐标.
(2)在直角坐标系中描出点M(2,4),N(-2,1) ,P(0,-4),
Q(4,-3).
解: (1)点A(2,1),B(-3,5),C(-4,0),
D(0,3),E(-3,-2),O(0,0).
(2)∵点M(2,4),∴先在x轴上找到坐标为2的点,并过这个点画x轴的垂线,再在y轴上找到坐标为4的点,并过这个点作y轴的垂线,这两条垂线的交点就是点M,同理可描出点N,P,Q.
课内练习
4.(1)在平面直角坐标系中画出点M(5,3)、A ,
C(-4.5,0)、D(0,-4)、H 、B(0,4) 、 E 、
F .
1 2 3 4 5 6
6
5
4
3
2
1
y
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
M(5,3)
D
C
B
E
F
课内练习
(2)请用彩色笔和直尺将其中七个点按照A→B→C→D→E→F→H→A的顺序依次连接起来;
(3)请为你的作品画出点睛之笔,并写出该点R的坐标.
-1
-2
-3
-4
-5
-6
1 2 3 4 5 6
4
3
2
1
y
-6 -5 -4 -3 -2 -1
x
B
E
F
A
C
D
R(-3,0)
H
5
6
O
课内练习
5.在平面直角坐标系中,若点P(m+2,m-3)在第四象限,求m的取值范围.
解析: 第四象限的点的横坐标为正,纵坐标为负.
解: ∵点P在第四象限,∴点P的横坐标为正,纵坐标为负,
∴
∴-2
m-3<0
课内练习
6.请在平面直角坐标系中描出下列各点:A(-2,-4),
B(5,3),C(0,4),D(-3,5),并指出各点所在的象限或坐标轴.
解: 各点在坐标系中的位置如解图.点A在第三象限,
点B在第一象限,点C在y轴上,点D在第二象限.
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
