4.6.1整式的加减 课件(共17张PPT)
文档属性
| 名称 | 4.6.1整式的加减 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-11 08:50:54 | ||
图片预览






文档简介
(共17张PPT)
4.6整式的加减
第1课时
浙教版 七年级上
旧知回顾
1.多项式 4a2+2a2b 7 共有几项(项数)?分别是什么?
4a2
2a2b
7
2.下列各题中的两项是不是同类项?
(1)2m2n和3mn2
(2)πr2和3r2
(2)和 2
3.已知4a2b3与a2mbn 1是同类项,则m=____,n=_____.
不是
是
是
1
4
新知导入
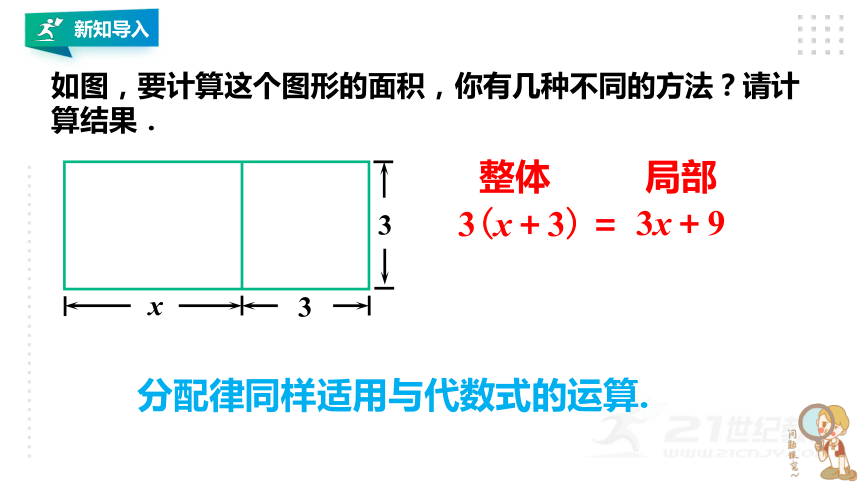
如图,要计算这个图形的面积,你有几种不同的方法?请计算结果.
3
3
x
整体
3(x+3)
局部
3x+9
=
分配律同样适用与代数式的运算.
新知讲解
根据分配律计算:
+(a b+c)
(a b+c)
=1×(a b+c)
=a b+c
= 1×(a b+c)
= a+b c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“ ”号,把括号和它前面的“ ”号去掉,括号里各项都改变符号.
课堂练习
1.去括号:
(1)+(a b)=__________;
(2) ( a b)=__________;
(3)+( a+b)=__________;
(4) (a+b)=__________;
(5) ( a+b)=__________;
(6) (a b)=__________;
a b
a+b
a+b
a b
a b
a+b
例题讲解
例1 将下列各式去括号:
(1)+(2a 3b)
(2) ( x+)
(3) (2x2 3x)
=2a 3b
=x
= ×2x2+( 3)×( 3x)
= x2+9x
例题讲解
例2 化简并求值:
2(a2 ab) (a2 ab),其中a= 2,b=3.
2a2 2ab
解:原式=
2a2+3ab
=ab
当a= 2,b=3时,
原式=ab=
( 2)×3
= 6
课堂练习
2.化简:
(1) x (x 3)
(2) (4x 6)+(6 3x)
= x+3
= 3x+5
课堂练习
2.化简:
(3)(x2 2x 2)+2(x2 1)
(4)2n (2 n)+(6n 2)
=x2+2x
=9n 4
课堂练习
3.化简并求值:
(a2b ab) (ab2 ba),其中a= ,b=2.
课堂练习
4.若x2 x=2,则(x2 2x) (1 x)的值是______.
1
5.已知a b= 3, c+d=2,则(b+c) (a d)的值
是______.
5
6.已知当x= 2时,代数式ax3+bx 7的值是5,求当
x=2时,该代数式的值.
19
课堂练习
7.已知一个代数式减去x2 y2等于x2+2y2,则这个代数式为
( )
(A) 3y2 (B) 2x2+y2
(C) 3y2 2x2 (D) 3y2
B
8.如果m是三次多项式,n也是三次多项式,那么m+n一定
是( )
(A) 六次多项式 (B) 次数不高于3的整式
(C) 三次多项式 (D) 次数不低于3的整式
B
课堂练习
9.如图①②所示为两种长方形铝合金窗框,已知窗框的长都是y(m),宽都是x(m)(不计铝合金的宽度).
(1)若一用户需要①型的窗框2个,②型的窗框5个,则共需要铝合金多少米?
(2)在(1)的条件下,当x=1.2,y=1.8时,求共需要铝合金的长度.
16x+14y
44.4
课堂总结
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“ ”号,把括号和它前面的“ ”号去掉,括号里各项都改变符号.
去括号法则的依据:
乘法分配律
作业布置
1.作业本1 4.6 整式的加减(1)
2.自主练习
https://www.21cnjy.com/help/help_extract.php
4.6整式的加减
第1课时
浙教版 七年级上
旧知回顾
1.多项式 4a2+2a2b 7 共有几项(项数)?分别是什么?
4a2
2a2b
7
2.下列各题中的两项是不是同类项?
(1)2m2n和3mn2
(2)πr2和3r2
(2)和 2
3.已知4a2b3与a2mbn 1是同类项,则m=____,n=_____.
不是
是
是
1
4
新知导入
如图,要计算这个图形的面积,你有几种不同的方法?请计算结果.
3
3
x
整体
3(x+3)
局部
3x+9
=
分配律同样适用与代数式的运算.
新知讲解
根据分配律计算:
+(a b+c)
(a b+c)
=1×(a b+c)
=a b+c
= 1×(a b+c)
= a+b c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“ ”号,把括号和它前面的“ ”号去掉,括号里各项都改变符号.
课堂练习
1.去括号:
(1)+(a b)=__________;
(2) ( a b)=__________;
(3)+( a+b)=__________;
(4) (a+b)=__________;
(5) ( a+b)=__________;
(6) (a b)=__________;
a b
a+b
a+b
a b
a b
a+b
例题讲解
例1 将下列各式去括号:
(1)+(2a 3b)
(2) ( x+)
(3) (2x2 3x)
=2a 3b
=x
= ×2x2+( 3)×( 3x)
= x2+9x
例题讲解
例2 化简并求值:
2(a2 ab) (a2 ab),其中a= 2,b=3.
2a2 2ab
解:原式=
2a2+3ab
=ab
当a= 2,b=3时,
原式=ab=
( 2)×3
= 6
课堂练习
2.化简:
(1) x (x 3)
(2) (4x 6)+(6 3x)
= x+3
= 3x+5
课堂练习
2.化简:
(3)(x2 2x 2)+2(x2 1)
(4)2n (2 n)+(6n 2)
=x2+2x
=9n 4
课堂练习
3.化简并求值:
(a2b ab) (ab2 ba),其中a= ,b=2.
课堂练习
4.若x2 x=2,则(x2 2x) (1 x)的值是______.
1
5.已知a b= 3, c+d=2,则(b+c) (a d)的值
是______.
5
6.已知当x= 2时,代数式ax3+bx 7的值是5,求当
x=2时,该代数式的值.
19
课堂练习
7.已知一个代数式减去x2 y2等于x2+2y2,则这个代数式为
( )
(A) 3y2 (B) 2x2+y2
(C) 3y2 2x2 (D) 3y2
B
8.如果m是三次多项式,n也是三次多项式,那么m+n一定
是( )
(A) 六次多项式 (B) 次数不高于3的整式
(C) 三次多项式 (D) 次数不低于3的整式
B
课堂练习
9.如图①②所示为两种长方形铝合金窗框,已知窗框的长都是y(m),宽都是x(m)(不计铝合金的宽度).
(1)若一用户需要①型的窗框2个,②型的窗框5个,则共需要铝合金多少米?
(2)在(1)的条件下,当x=1.2,y=1.8时,求共需要铝合金的长度.
16x+14y
44.4
课堂总结
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“ ”号,把括号和它前面的“ ”号去掉,括号里各项都改变符号.
去括号法则的依据:
乘法分配律
作业布置
1.作业本1 4.6 整式的加减(1)
2.自主练习
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
