第3章 圆的基本性质 阅读材料 美妙的镶嵌 课件(24张PPT)
文档属性
| 名称 | 第3章 圆的基本性质 阅读材料 美妙的镶嵌 课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 10:52:31 | ||
图片预览


文档简介
(共24张PPT)
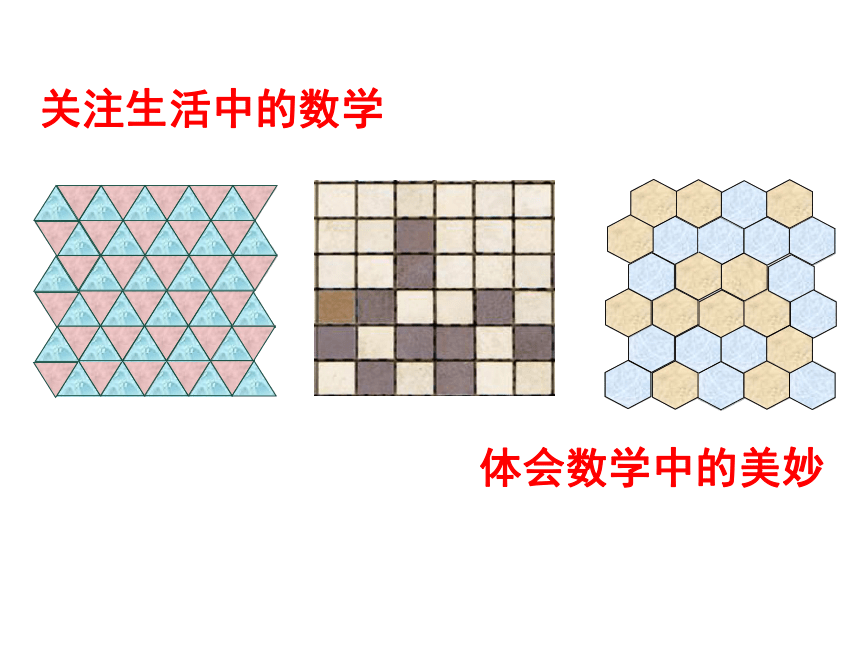
《美妙的镶嵌》
阅读材料:
关注生活中的数学
体会数学中的美妙
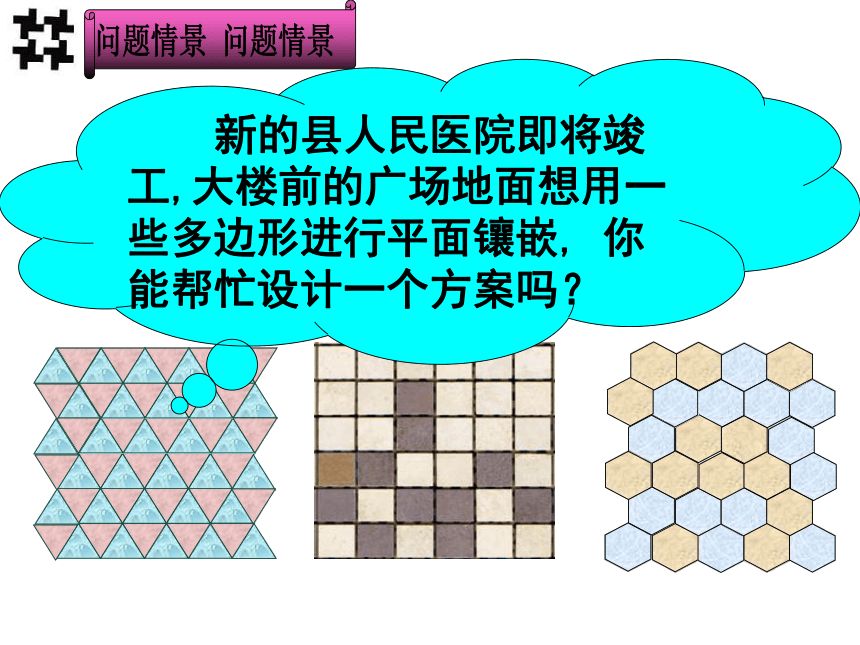
新的县人民医院即将竣工,大楼前的广场地面想用一些多边形进行平面镶嵌, 你能帮忙设计一个方案吗?
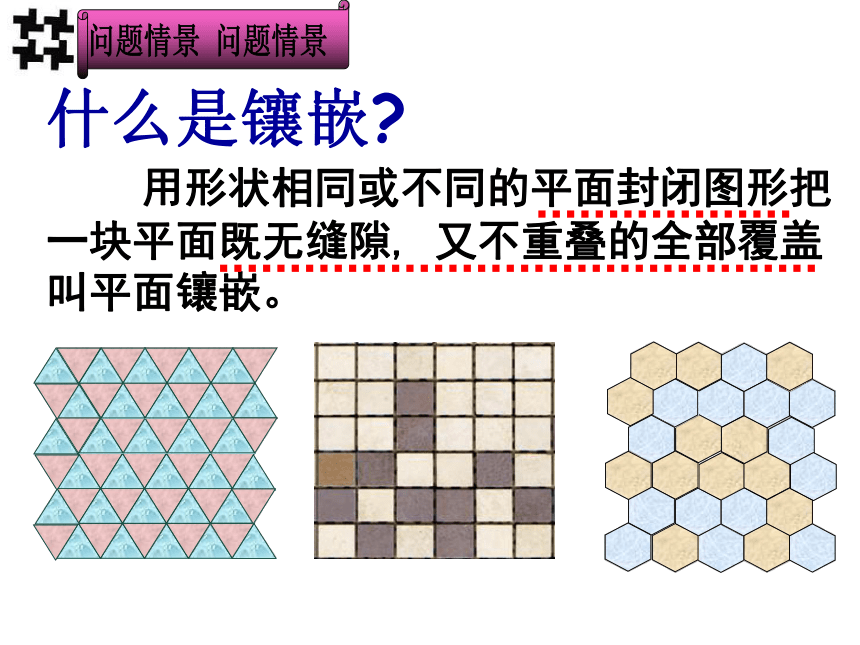
什么是镶嵌
用形状相同或不同的平面封闭图形把一块平面既无缝隙, 又不重叠的全部覆盖叫平面镶嵌。
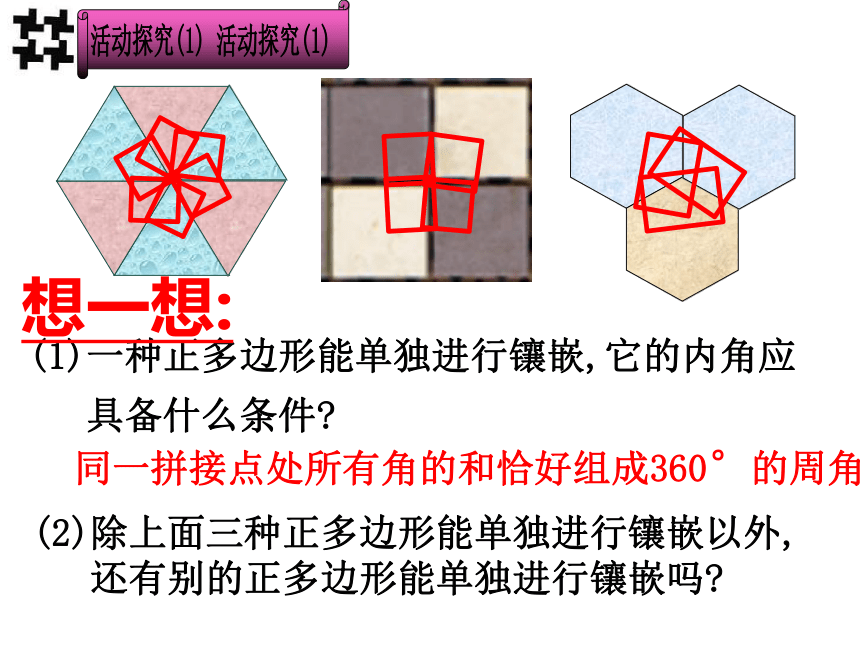
(1)一种正多边形能单独进行镶嵌,它的内角应
具备什么条件
想一想:
(2)除上面三种正多边形能单独进行镶嵌以外,
还有别的正多边形能单独进行镶嵌吗
同一拼接点处所有角的和恰好组成360°的周角。
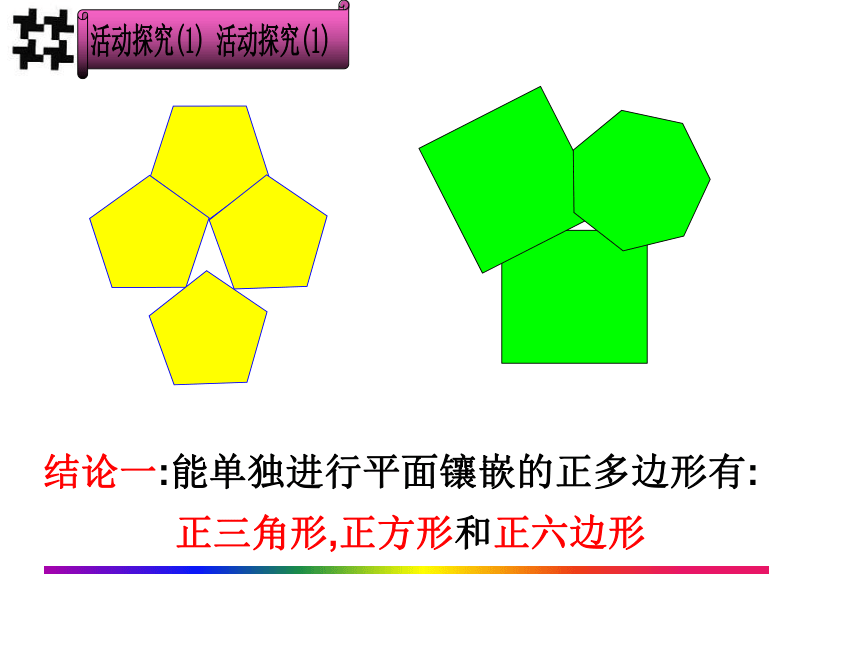
结论一:能单独进行平面镶嵌的正多边形有:
正三角形,正方形和正六边形
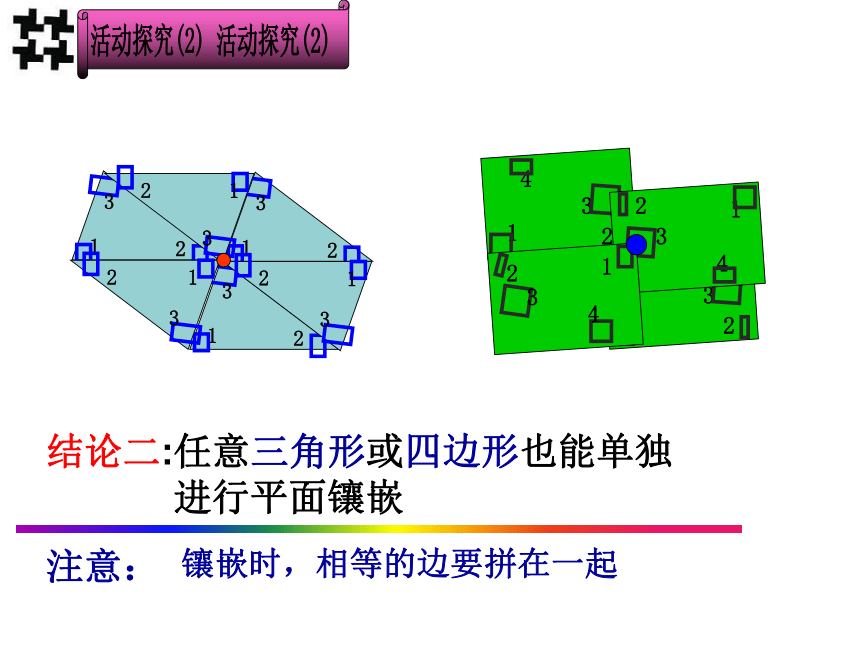
医院广场的地面如果用任意的全等三角形或四边形单独进行平面镶嵌,可以吗
(请大家按小组利用学具袋中的任意全等三角
形和四边形进行探索。)
同一拼接点处所有角的和恰好组成360°的周角。
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
结论二:任意三角形或四边形也能单独
进行平面镶嵌
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
注意:
镶嵌时,相等的边要拼在一起
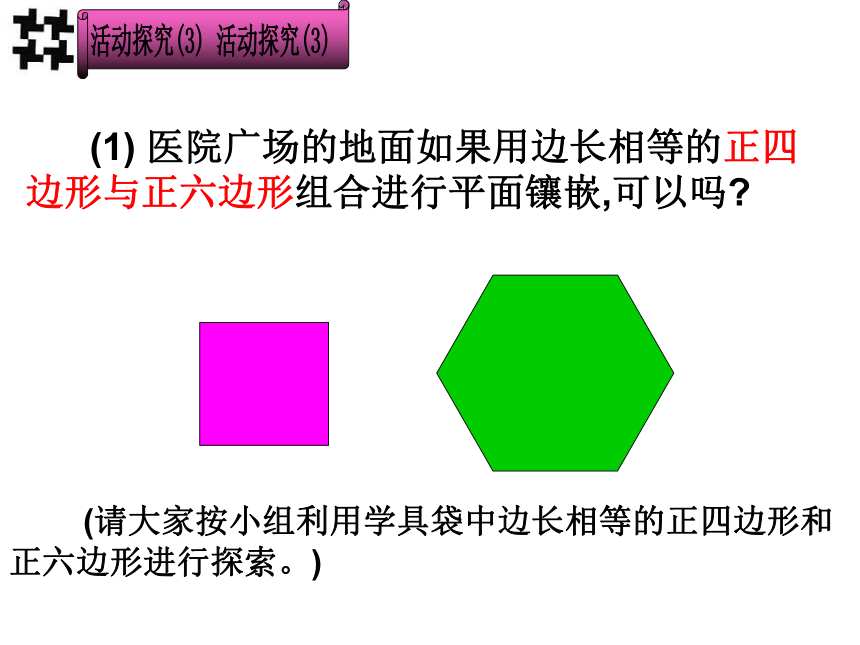
(1) 医院广场的地面如果用边长相等的正四边形与正六边形组合进行平面镶嵌,可以吗
(请大家按小组利用学具袋中边长相等的正四边形和
正六边形进行探索。)
(2) 医院广场的地面如果用边长相等的两种正多边形进行平面镶嵌,可以吗 共有几种组合
……
1)正三角形与正方形的平面镶嵌
(4 3 4 3 3)
(3 3 3 4 4)
2) 正三角形与正六边形的平面镶嵌
(3 3 3 3 6)
(3 6 3 6)
(4 8 8)
3)正四边形与正八边形的平面镶嵌
(12 12 3)
4)正三角形与正十二边形的平面镶嵌
结论3:用两种正多边形进行平面镶嵌, 我们发现了5种可能:
(3个)正三角形+(2个)正方形
(4个)正三角形+(1个)正六边形
(2个)正三角形+(2个)正六边形
(1个)正三角形+(2个)正十二边形
(1个)正方形 + (2个)正八边形
医院广场的地面如果用边长相等的三种正多边形进行平面镶嵌,可以有哪些组合
……
不用拼图,你能利用所学知识来判断三种
正多边形能否进行平面镶嵌
正十二边形与正方形、正六边形的平面镶嵌
正三角形与正方形、正六边形的平面镶嵌
医院广场的地面如果用边长相等的三种正多边形进行平面镶嵌,可以有哪些组合
资料:用正多边形进行平面镶嵌只有以下这16组解。有书记载说明这16组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
新的县人民医院即将竣工,大楼前的广场地面想用一些多边形进行平面镶嵌, 你能帮忙设计一个方案吗?
埃舍尔的作品——鸟分割的平面
艺术化的设计制作镶嵌:
镶嵌的提高
埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。他是一个将艺术与数学融合的画家,也因此享誉世界。
资 料
埃舍尔的作品
欣 赏
收获与启示
(2) 用两种多边形镶嵌的规律: 拼接在同一
个点的各个角的和恰好等于360°(周角)
(注意检验)
(1)用一种多边形镶嵌的规律:拼接在同一个
点的各个角的和恰好等于360°(周角)
请你用本节课所学知识,用8开素描纸设计一幅镶嵌艺术画.
《美妙的镶嵌》
阅读材料:
关注生活中的数学
体会数学中的美妙
新的县人民医院即将竣工,大楼前的广场地面想用一些多边形进行平面镶嵌, 你能帮忙设计一个方案吗?
什么是镶嵌
用形状相同或不同的平面封闭图形把一块平面既无缝隙, 又不重叠的全部覆盖叫平面镶嵌。
(1)一种正多边形能单独进行镶嵌,它的内角应
具备什么条件
想一想:
(2)除上面三种正多边形能单独进行镶嵌以外,
还有别的正多边形能单独进行镶嵌吗
同一拼接点处所有角的和恰好组成360°的周角。
结论一:能单独进行平面镶嵌的正多边形有:
正三角形,正方形和正六边形
医院广场的地面如果用任意的全等三角形或四边形单独进行平面镶嵌,可以吗
(请大家按小组利用学具袋中的任意全等三角
形和四边形进行探索。)
同一拼接点处所有角的和恰好组成360°的周角。
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
结论二:任意三角形或四边形也能单独
进行平面镶嵌
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
注意:
镶嵌时,相等的边要拼在一起
(1) 医院广场的地面如果用边长相等的正四边形与正六边形组合进行平面镶嵌,可以吗
(请大家按小组利用学具袋中边长相等的正四边形和
正六边形进行探索。)
(2) 医院广场的地面如果用边长相等的两种正多边形进行平面镶嵌,可以吗 共有几种组合
……
1)正三角形与正方形的平面镶嵌
(4 3 4 3 3)
(3 3 3 4 4)
2) 正三角形与正六边形的平面镶嵌
(3 3 3 3 6)
(3 6 3 6)
(4 8 8)
3)正四边形与正八边形的平面镶嵌
(12 12 3)
4)正三角形与正十二边形的平面镶嵌
结论3:用两种正多边形进行平面镶嵌, 我们发现了5种可能:
(3个)正三角形+(2个)正方形
(4个)正三角形+(1个)正六边形
(2个)正三角形+(2个)正六边形
(1个)正三角形+(2个)正十二边形
(1个)正方形 + (2个)正八边形
医院广场的地面如果用边长相等的三种正多边形进行平面镶嵌,可以有哪些组合
……
不用拼图,你能利用所学知识来判断三种
正多边形能否进行平面镶嵌
正十二边形与正方形、正六边形的平面镶嵌
正三角形与正方形、正六边形的平面镶嵌
医院广场的地面如果用边长相等的三种正多边形进行平面镶嵌,可以有哪些组合
资料:用正多边形进行平面镶嵌只有以下这16组解。有书记载说明这16组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
新的县人民医院即将竣工,大楼前的广场地面想用一些多边形进行平面镶嵌, 你能帮忙设计一个方案吗?
埃舍尔的作品——鸟分割的平面
艺术化的设计制作镶嵌:
镶嵌的提高
埃舍尔(M.C.ESCHER1898-1972)荷兰现代版画艺术家。他是一个将艺术与数学融合的画家,也因此享誉世界。
资 料
埃舍尔的作品
欣 赏
收获与启示
(2) 用两种多边形镶嵌的规律: 拼接在同一
个点的各个角的和恰好等于360°(周角)
(注意检验)
(1)用一种多边形镶嵌的规律:拼接在同一个
点的各个角的和恰好等于360°(周角)
请你用本节课所学知识,用8开素描纸设计一幅镶嵌艺术画.
同课章节目录
