3.8 弧长及扇形的面积 课件(15张PPT)
文档属性
| 名称 | 3.8 弧长及扇形的面积 课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 727.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 11:52:29 | ||
图片预览




文档简介
(共15张PPT)
弧长及扇形的面积
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1
跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要确保这些弯道的“展直长度”是一样的.
甲
乙
1
2
与弧长相关的计算
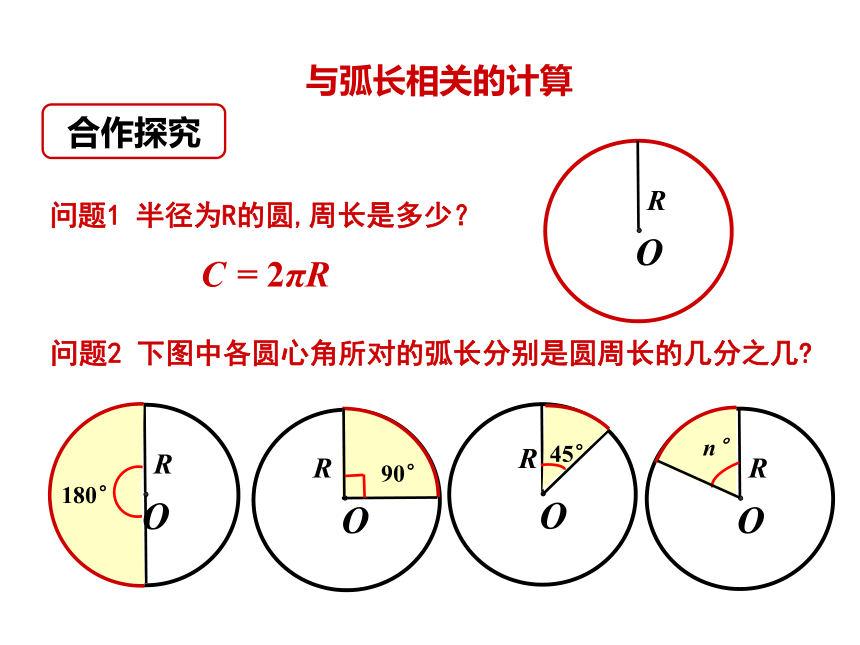
问题1 半径为R的圆,周长是多少?
O
R
问题2 下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
45°
O
R
n°
O
R
90°
O
R
180°
合作探究
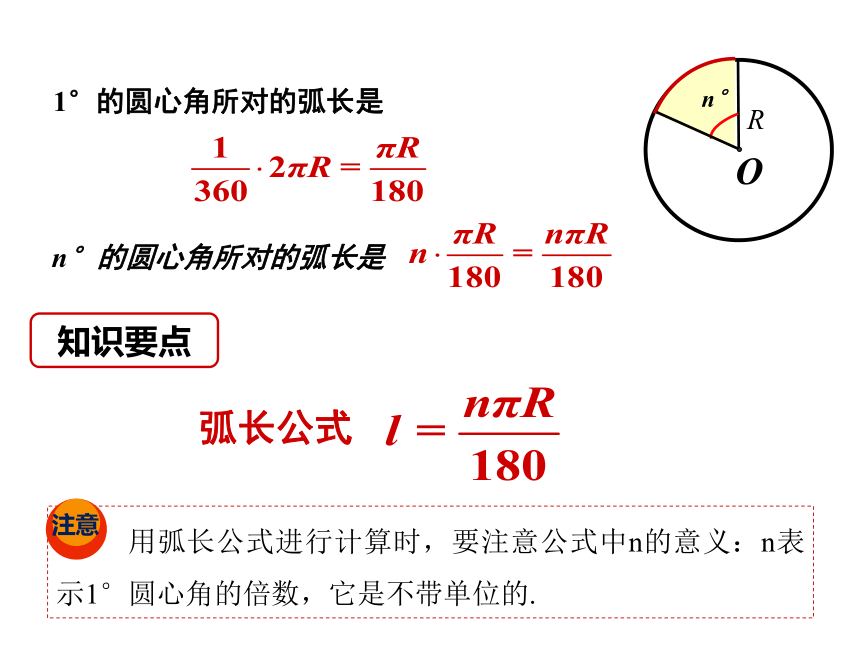
1°的圆心角所对的弧长是
n°的圆心角所对的弧长是
O
R
n°
知识要点
弧长公式
用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
注意
1. 半径为10cm的圆,100°的圆心角所对的弧长是
_________cm.
2. 若圆的半径为R,弧长等于 ,则该弧所对的圆
心角为 .
3. 在半径为Rcm的圆中,150°的圆心角所对的弧长
等于10 cm,则R= .
60°
12cm
练一练
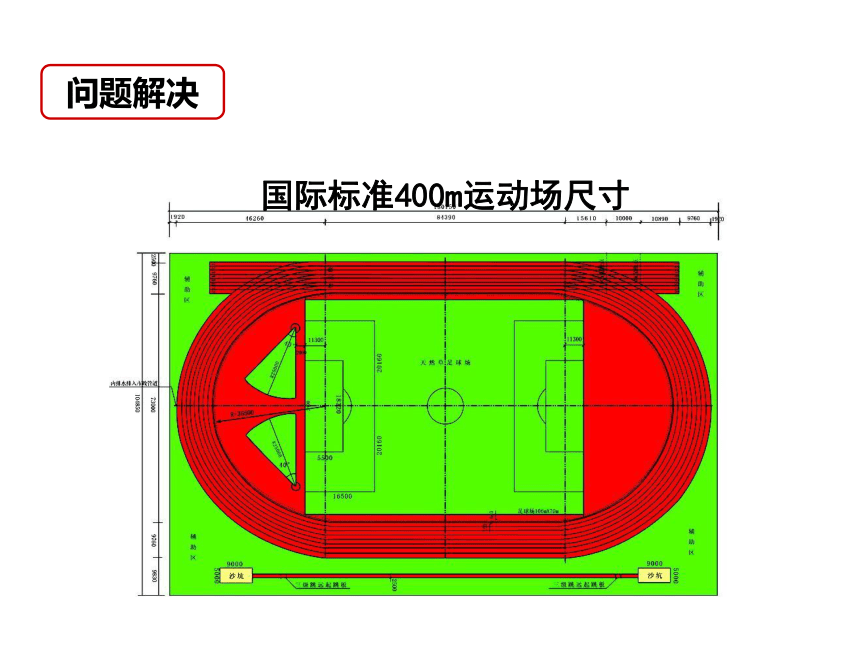
问题解决
国际标准400m运动场尺寸
面积是多少?
问题1 半径为R的圆,
O
R
问题2 圆心角为n°的扇形面积是
类比学习
与扇形面积相关的计算
O
R
n°
圆心角为1°的扇形面积是
圆心角为n°的扇形面积是
知识要点
扇形面积公式
O
R
n°
类比学习
发现
弧长公式:
扇形面积公式:
2. 比较扇形面积公式与弧长公式,可用弧长来表示
扇形的面积:
1. 弧长和扇形的面积都由扇形的半径和扇形的圆心
角决定的.
比较发现
1. 一个扇形的圆心角为90o,半径为2cm,则弧长
为_____cm,扇形面积为_______cm2.
3. 已知扇形的半径为6,面积为12 ,则扇形的弧
长是( )
A. 3 B. 4 C. 5 D. 6
2. 一个扇形的半径为24cm,面积是240 cm2,则
该扇形的圆心角为_______.
150o
B
练一练
如图,一根 长 的绳子,一端栓在柱子上,另一端栓着一只小羊, 小羊活动的最大区域面积是 m2.
5
3m
5m
学以致用
6m
巩固提升
如图,正方形ABCD的边长为2,扇形ABD和扇形CBD
是以A、C为圆心,2为半径的圆的一部分,求阴影部分
的面积.
1、弧长计算公式:
2、扇形面积计算公式:
类比推导
3、应用公式解决问题
谢 谢!
如图,正方形ABCD的对角线AC=2厘米,扇形ACB
是以AC为直径的半圆,扇形DAC是以D为圆心,AD
为半径的圆的一部分,求阴影部分的面积.
巩固提升
弧长及扇形的面积
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1
跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要确保这些弯道的“展直长度”是一样的.
甲
乙
1
2
与弧长相关的计算
问题1 半径为R的圆,周长是多少?
O
R
问题2 下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
45°
O
R
n°
O
R
90°
O
R
180°
合作探究
1°的圆心角所对的弧长是
n°的圆心角所对的弧长是
O
R
n°
知识要点
弧长公式
用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
注意
1. 半径为10cm的圆,100°的圆心角所对的弧长是
_________cm.
2. 若圆的半径为R,弧长等于 ,则该弧所对的圆
心角为 .
3. 在半径为Rcm的圆中,150°的圆心角所对的弧长
等于10 cm,则R= .
60°
12cm
练一练
问题解决
国际标准400m运动场尺寸
面积是多少?
问题1 半径为R的圆,
O
R
问题2 圆心角为n°的扇形面积是
类比学习
与扇形面积相关的计算
O
R
n°
圆心角为1°的扇形面积是
圆心角为n°的扇形面积是
知识要点
扇形面积公式
O
R
n°
类比学习
发现
弧长公式:
扇形面积公式:
2. 比较扇形面积公式与弧长公式,可用弧长来表示
扇形的面积:
1. 弧长和扇形的面积都由扇形的半径和扇形的圆心
角决定的.
比较发现
1. 一个扇形的圆心角为90o,半径为2cm,则弧长
为_____cm,扇形面积为_______cm2.
3. 已知扇形的半径为6,面积为12 ,则扇形的弧
长是( )
A. 3 B. 4 C. 5 D. 6
2. 一个扇形的半径为24cm,面积是240 cm2,则
该扇形的圆心角为_______.
150o
B
练一练
如图,一根 长 的绳子,一端栓在柱子上,另一端栓着一只小羊, 小羊活动的最大区域面积是 m2.
5
3m
5m
学以致用
6m
巩固提升
如图,正方形ABCD的边长为2,扇形ABD和扇形CBD
是以A、C为圆心,2为半径的圆的一部分,求阴影部分
的面积.
1、弧长计算公式:
2、扇形面积计算公式:
类比推导
3、应用公式解决问题
谢 谢!
如图,正方形ABCD的对角线AC=2厘米,扇形ACB
是以AC为直径的半圆,扇形DAC是以D为圆心,AD
为半径的圆的一部分,求阴影部分的面积.
巩固提升
同课章节目录
