浙教版数学九年级上册 第四章 相似三角形 一线三等角相似专题课(共17张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 第四章 相似三角形 一线三等角相似专题课(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 170.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 11:52:29 | ||
图片预览


文档简介
(共17张PPT)
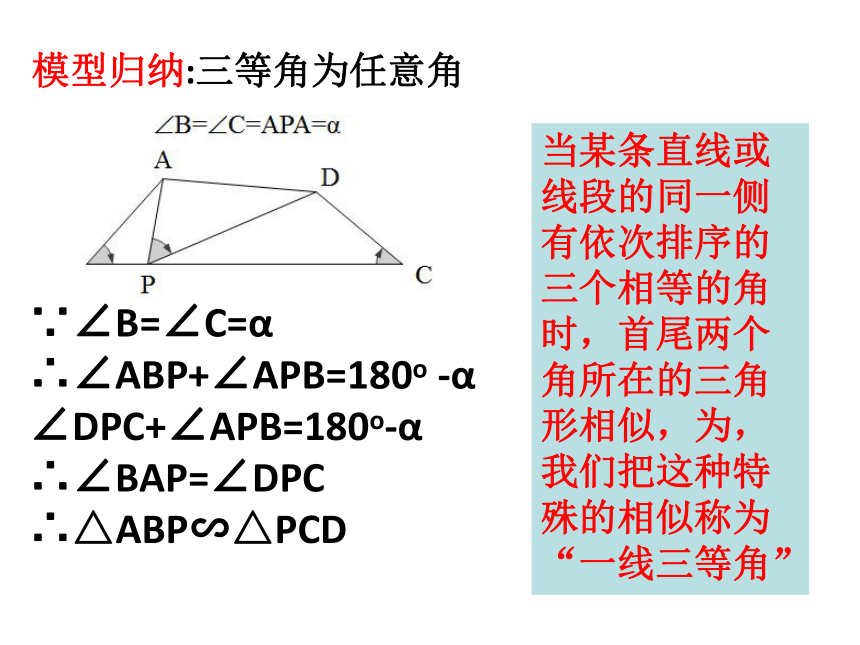
(1)点E为BC上任意一点,若 ∠B= ∠C=60°, ∠AEF= ∠ C,则△ABE与△ ECF的关系还成立吗?说明理由
(2)点E为BC上任意一点若 ∠B= ∠C= α, ∠AEF= ∠ C,则△ABE 与△ ECF的关系还成立吗?
C
60°
60°
60°
A
B
E
F
α
α
α
A
B
C
E
F
α
α
α
A
B
F
C
E
60°
60°
60°
C
A
B
E
F
“一线三等角”型相似
问题发现 知识整理
△ABE∽ △ECF
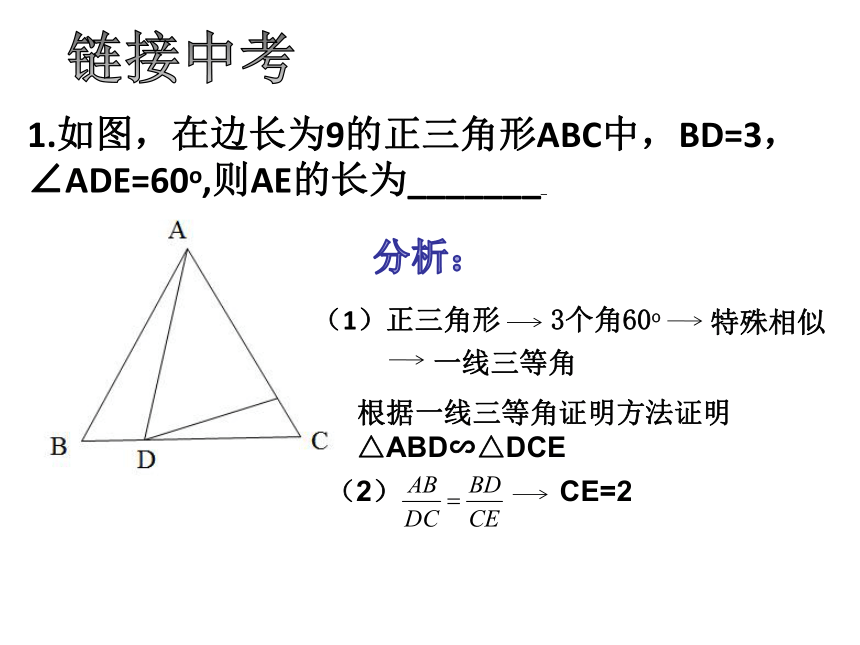
模型归纳:三等角为任意角
∵∠B=∠C=α
∴∠ABP+∠APB=180o -α
∠DPC+∠APB=180o-α
∴∠BAP=∠DPC
∴△ABP∽△PCD
当某条直线或线段的同一侧有依次排序的三个相等的角时,首尾两个角所在的三角形相似,为,我们把这种特殊的相似称为“一线三等角”
链接中考
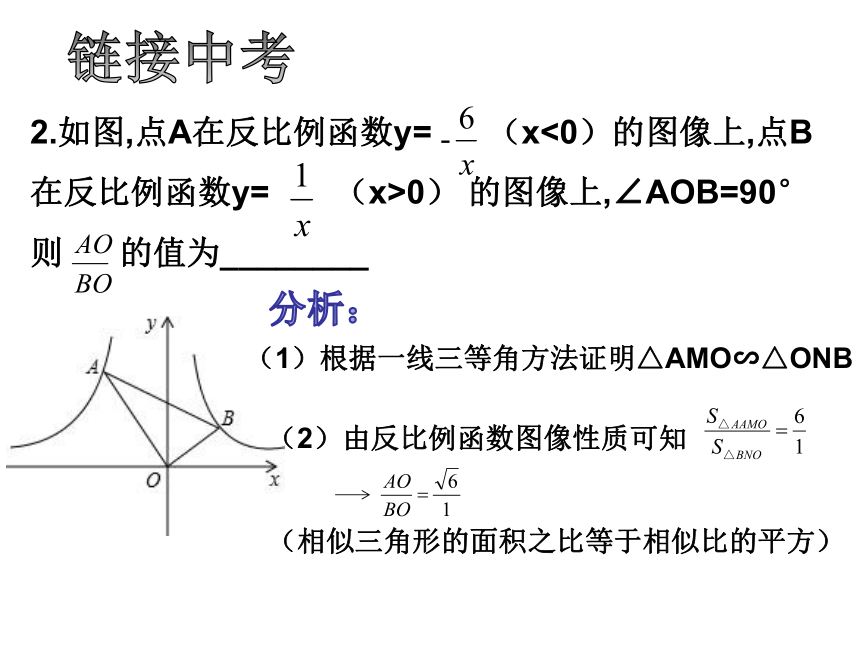
1.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60o,则AE的长为________
分析:
(1)正三角形
3个角60o
特殊相似
一线三等角
根据一线三等角证明方法证明△ABD∽△DCE
(2) CE=2
链接中考
2.如图,点A在反比例函数y= (x<0)的图像上,点B在反比例函数y= (x>0) 的图像上,∠AOB=90°则 的值为________
分析:
(1)根据一线三等角方法证明△AMO∽△ONB
(2)由反比例函数图像性质可知
(相似三角形的面积之比等于相似比的平方)
A
B
C
E
F
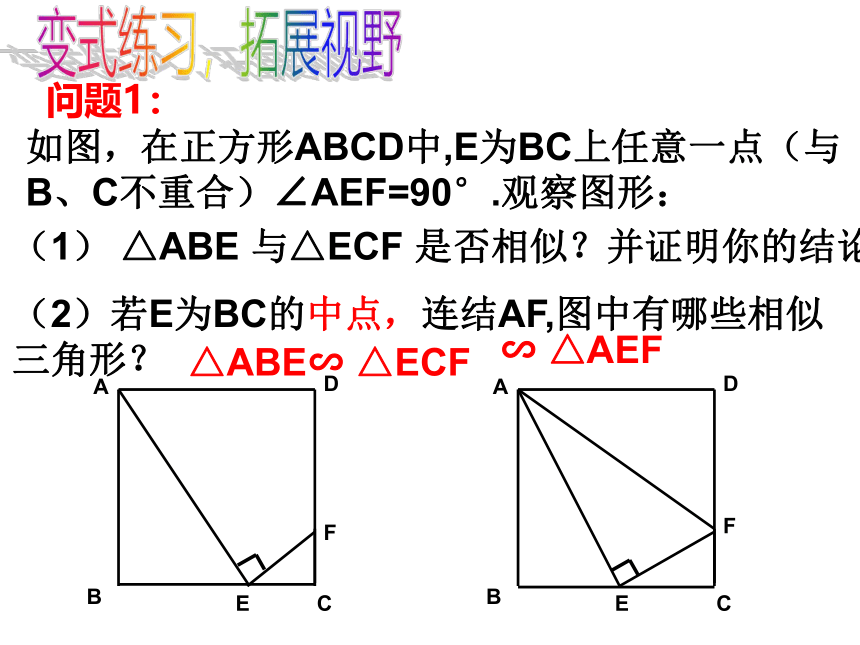
如图,在正方形ABCD中,E为BC上任意一点(与B、C不重合)∠AEF=90°.观察图形:
D
A
B
C
E
F
D
(2)若E为BC的中点,连结AF,图中有哪些相似三角形?
(1) △ABE 与△ECF 是否相似?并证明你的结论。
变式练习,拓展视野
△ABE∽ △ECF
∽ △AEF
问题1:
A
B
C
E
F
α
α
α
D
A
F
α
B
C
E
α
α
D
G
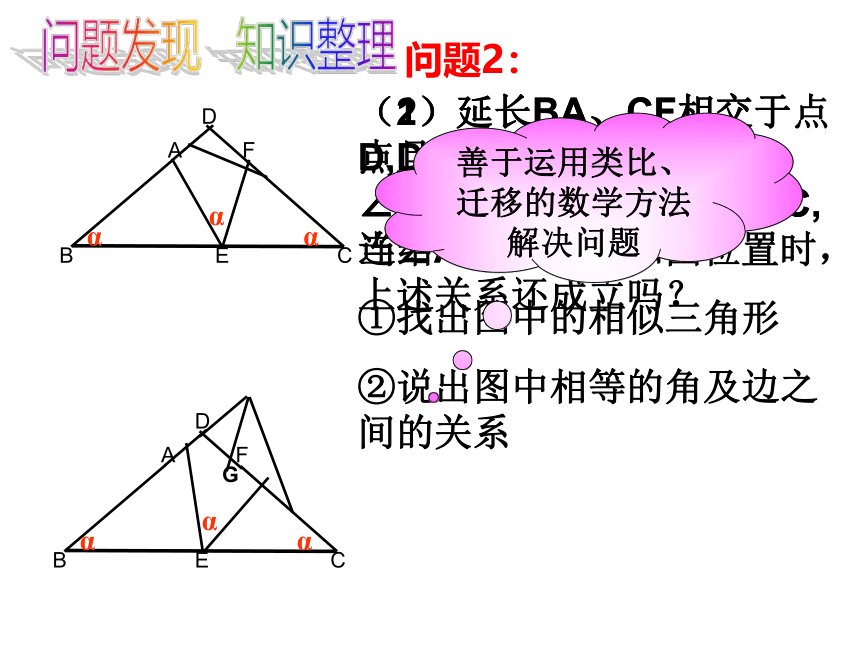
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
问题发现 知识整理
问题2:
善于运用类比、迁移的数学方法解决问题
C
A
B
E
F
A
B
C
E
F
A
B
C
E
F
α
α
α
A
B
C
E
F
α
α
α
D
①
②
③
①
②
①
②
③
①
②
E为中点
归纳:
变式:.在直角梯形ABCF中,,CB=14,CF=4, AB=6,,CF∥AB,在边CB上找一点E,使以E、A、B为顶点的三角形和以E、C、F为顶点的三角形相似,则CE=_______
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E重合,若AD=10, AB= 8,
则EF=______
善于在复杂图形中寻找基本型
5
A
D
B
C
E
F
A
B
C
F
E
E
E
5.6或2或12
注意分类讨论的数学思想
实战演练 知识运用
E
B
C
D
F
2.已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
7
A
实战演练 知识运用
E
B
C
D
F
A
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的中点, 且∠EDF =∠C,
(1) 若BE·CF=48,则AB=_____
(2)在(1)的条件下,若EF=m,
则S△DEF =_______
利用转化的
数学思想
H
P
8
实战演练 知识运用
(1)连接AP、AQ、PQ,试判断△APQ的形状,并说明理由。
(2)当t=1秒时,连接AC,与PQ相交于点K.求AK的长。
Q
P
A
B
C
D
K
善于在复杂图形中寻找基本型
已知:菱形ABCD,AB=4m, ∠B=60°,点P、Q分别从点B、C出发,沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒.
迁移拓展 知识提升
E
Q
A
B
C
D
P
N
F
(3) 当t=2秒时,连接AP、PQ,将∠APQ逆时针旋转,使角的两边与AB、AD、AC分别交于点E、N、F,连接EF.若AN=1,求S△EPF.
注意运用转化的数学思想
迁移拓展 知识提升
(4)以OS为一边在∠SOC内作∠SOT,使
∠SOT = ∠BDC,OT边交BC的延长线于点T,
若BT=4.8,求AK的长。
A
S
K
D
C
B
o
T
30 °
30 °
30 °
迁移拓展 知识提升
(P)
(Q)
P
Q
我的收获
C
A
B
E
D
C
A
B
E
D
C
A
B
E
D
A
B
C
E
D
α
α
α
A
B
C
E
D
F
α
α
α
α
α
α
O
A
B
C
D
P
善于观察 善于发现 善于总结
1、已知:等边△ABC 中,P为直线AC上一动点,连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时,证明PA·PC=AB ·CN
(2)若P在AC的延长线上,上述关系是否成立?
(3)若P在CA的延长线上, CN=1.5,BC=2,求AP、BP的长
补充练习、内化理解
N
B
C
A
Q
N
B
C
A
Q
N
B
C
A
Q
P
60°
60°
60°
P
P
如图,L1,L2,L3是同一平面内的三条平行直线,L1与L2间的距离是1,L2与L3间的距离是2,正三角形ABC的三顶点分别在L1,L2,L3上,求△ABC的边长
(1)点E为BC上任意一点,若 ∠B= ∠C=60°, ∠AEF= ∠ C,则△ABE与△ ECF的关系还成立吗?说明理由
(2)点E为BC上任意一点若 ∠B= ∠C= α, ∠AEF= ∠ C,则△ABE 与△ ECF的关系还成立吗?
C
60°
60°
60°
A
B
E
F
α
α
α
A
B
C
E
F
α
α
α
A
B
F
C
E
60°
60°
60°
C
A
B
E
F
“一线三等角”型相似
问题发现 知识整理
△ABE∽ △ECF
模型归纳:三等角为任意角
∵∠B=∠C=α
∴∠ABP+∠APB=180o -α
∠DPC+∠APB=180o-α
∴∠BAP=∠DPC
∴△ABP∽△PCD
当某条直线或线段的同一侧有依次排序的三个相等的角时,首尾两个角所在的三角形相似,为,我们把这种特殊的相似称为“一线三等角”
链接中考
1.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60o,则AE的长为________
分析:
(1)正三角形
3个角60o
特殊相似
一线三等角
根据一线三等角证明方法证明△ABD∽△DCE
(2) CE=2
链接中考
2.如图,点A在反比例函数y= (x<0)的图像上,点B在反比例函数y= (x>0) 的图像上,∠AOB=90°则 的值为________
分析:
(1)根据一线三等角方法证明△AMO∽△ONB
(2)由反比例函数图像性质可知
(相似三角形的面积之比等于相似比的平方)
A
B
C
E
F
如图,在正方形ABCD中,E为BC上任意一点(与B、C不重合)∠AEF=90°.观察图形:
D
A
B
C
E
F
D
(2)若E为BC的中点,连结AF,图中有哪些相似三角形?
(1) △ABE 与△ECF 是否相似?并证明你的结论。
变式练习,拓展视野
△ABE∽ △ECF
∽ △AEF
问题1:
A
B
C
E
F
α
α
α
D
A
F
α
B
C
E
α
α
D
G
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
问题发现 知识整理
问题2:
善于运用类比、迁移的数学方法解决问题
C
A
B
E
F
A
B
C
E
F
A
B
C
E
F
α
α
α
A
B
C
E
F
α
α
α
D
①
②
③
①
②
①
②
③
①
②
E为中点
归纳:
变式:.在直角梯形ABCF中,,CB=14,CF=4, AB=6,,CF∥AB,在边CB上找一点E,使以E、A、B为顶点的三角形和以E、C、F为顶点的三角形相似,则CE=_______
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E重合,若AD=10, AB= 8,
则EF=______
善于在复杂图形中寻找基本型
5
A
D
B
C
E
F
A
B
C
F
E
E
E
5.6或2或12
注意分类讨论的数学思想
实战演练 知识运用
E
B
C
D
F
2.已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
7
A
实战演练 知识运用
E
B
C
D
F
A
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的中点, 且∠EDF =∠C,
(1) 若BE·CF=48,则AB=_____
(2)在(1)的条件下,若EF=m,
则S△DEF =_______
利用转化的
数学思想
H
P
8
实战演练 知识运用
(1)连接AP、AQ、PQ,试判断△APQ的形状,并说明理由。
(2)当t=1秒时,连接AC,与PQ相交于点K.求AK的长。
Q
P
A
B
C
D
K
善于在复杂图形中寻找基本型
已知:菱形ABCD,AB=4m, ∠B=60°,点P、Q分别从点B、C出发,沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒.
迁移拓展 知识提升
E
Q
A
B
C
D
P
N
F
(3) 当t=2秒时,连接AP、PQ,将∠APQ逆时针旋转,使角的两边与AB、AD、AC分别交于点E、N、F,连接EF.若AN=1,求S△EPF.
注意运用转化的数学思想
迁移拓展 知识提升
(4)以OS为一边在∠SOC内作∠SOT,使
∠SOT = ∠BDC,OT边交BC的延长线于点T,
若BT=4.8,求AK的长。
A
S
K
D
C
B
o
T
30 °
30 °
30 °
迁移拓展 知识提升
(P)
(Q)
P
Q
我的收获
C
A
B
E
D
C
A
B
E
D
C
A
B
E
D
A
B
C
E
D
α
α
α
A
B
C
E
D
F
α
α
α
α
α
α
O
A
B
C
D
P
善于观察 善于发现 善于总结
1、已知:等边△ABC 中,P为直线AC上一动点,连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时,证明PA·PC=AB ·CN
(2)若P在AC的延长线上,上述关系是否成立?
(3)若P在CA的延长线上, CN=1.5,BC=2,求AP、BP的长
补充练习、内化理解
N
B
C
A
Q
N
B
C
A
Q
N
B
C
A
Q
P
60°
60°
60°
P
P
如图,L1,L2,L3是同一平面内的三条平行直线,L1与L2间的距离是1,L2与L3间的距离是2,正三角形ABC的三顶点分别在L1,L2,L3上,求△ABC的边长
同课章节目录
