浙教版八年级数学上册 第2章 特殊三角形 复习课件(共23张PPT)
文档属性
| 名称 | 浙教版八年级数学上册 第2章 特殊三角形 复习课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 292.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 14:03:40 | ||
图片预览




文档简介
(共23张PPT)
第2章 特殊三角形
复习课件
特殊三角形
两个锐角互余
直角三角形斜边上的中线等于斜边的一半
勾股定理
直角三角形的性质
直角三角形的判定
两个直角三角形全等的判定方法:HL
有关角平分线的性质:角的内部,到角两边距离相等的点,在这个角的平分线上
等腰直角三角形
有两个角互余的三角形是直角三角形
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形
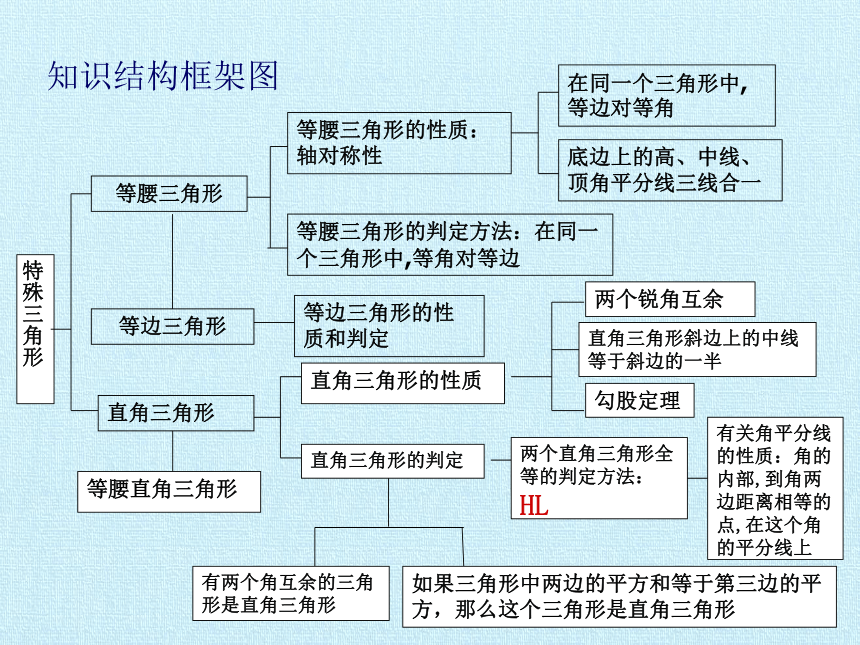
知识结构框架图
等边三角形
等腰三角形
等腰三角形的性质:轴对称性
等腰三角形的判定方法:在同一个三角形中,等角对等边
在同一个三角形中,等边对等角
底边上的高、中线、顶角平分线三线合一
直角三角形
等边三角形的性质和判定
1.什么是等腰三角形
有两边相等的三角形叫做等腰三角形
练1已知等腰三角形的两边长分别是4和6,则它的周长是________。
练2已知等腰三角形的两边长分别是3和6,则它的周长是________。
练3已知等腰三角形一腰上的中线将它的周长分成15cm和6cm两部分,则等腰三角形的底边长是__________。
14或16
15
1cm
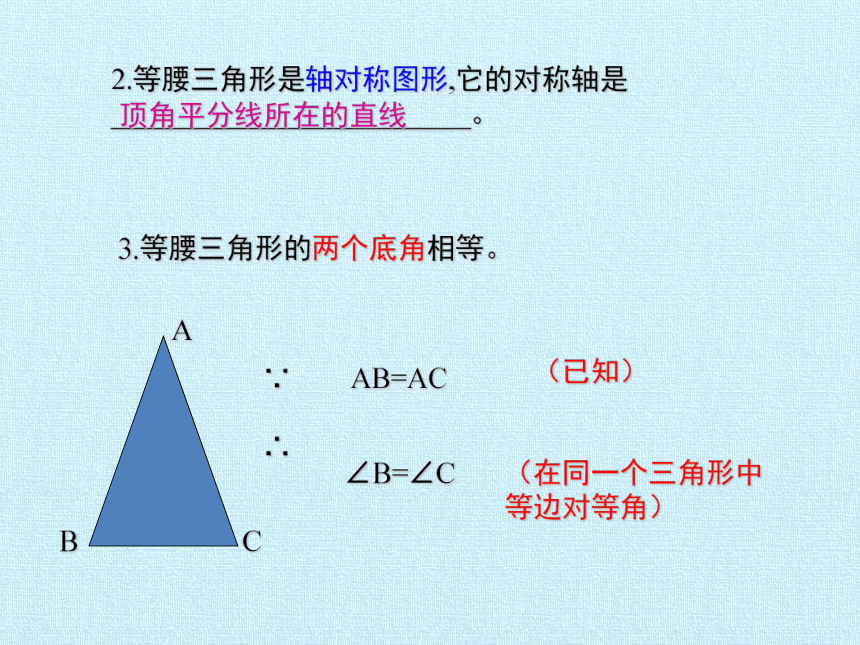
2.等腰三角形是轴对称图形,它的对称轴是_________________________。
3.等腰三角形的两个底角相等。
A
C
B
∵
∴
AB=AC
∠B=∠C
(在同一个三角形中
等边对等角)
(已知)
顶角平分线所在的直线
练4:已知等腰三角形的一个底角是300,则它的顶角是__________。
练5:已知等腰三角形的一个角是300,则它的顶角是__________。
练6:已知等腰三角形的一个角是1300,则它的顶角是__________。
练7:已知等腰三角形的顶角是底角的2倍,则它的底角是__________。
1200
1200或300
1300
450
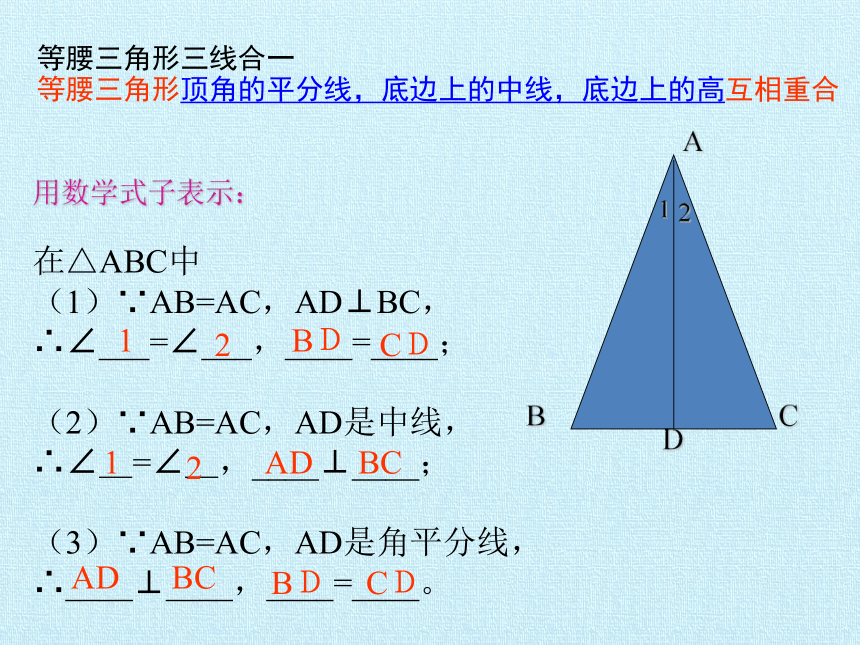
等腰三角形三线合一
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
用数学式子表示:
A
C
B
D
1
2
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
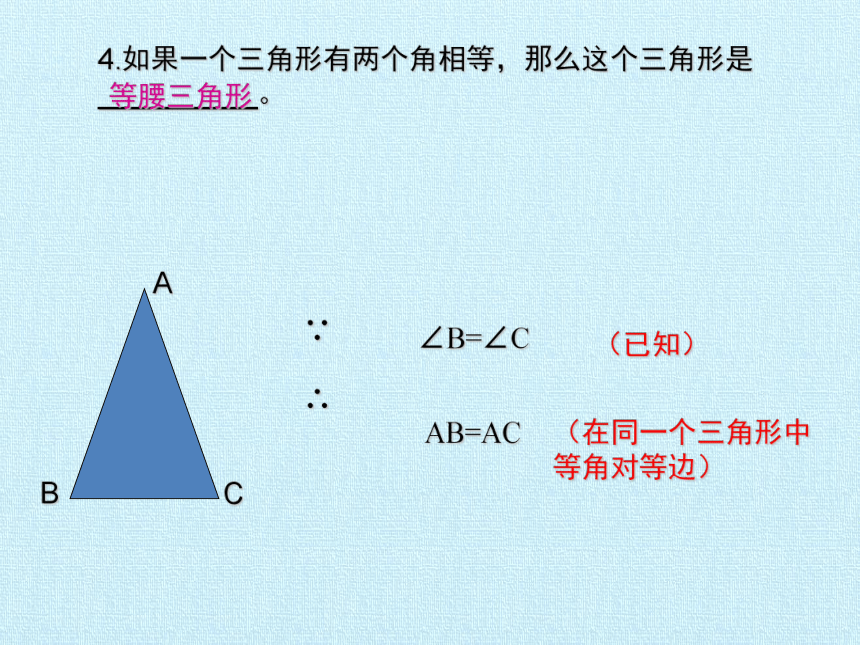
4.如果一个三角形有两个角相等,那么这个三角形是__________。
A
C
B
∵
∴
AB=AC
∠B=∠C
(在同一个三角形中
等角对等边)
(已知)
等腰三角形
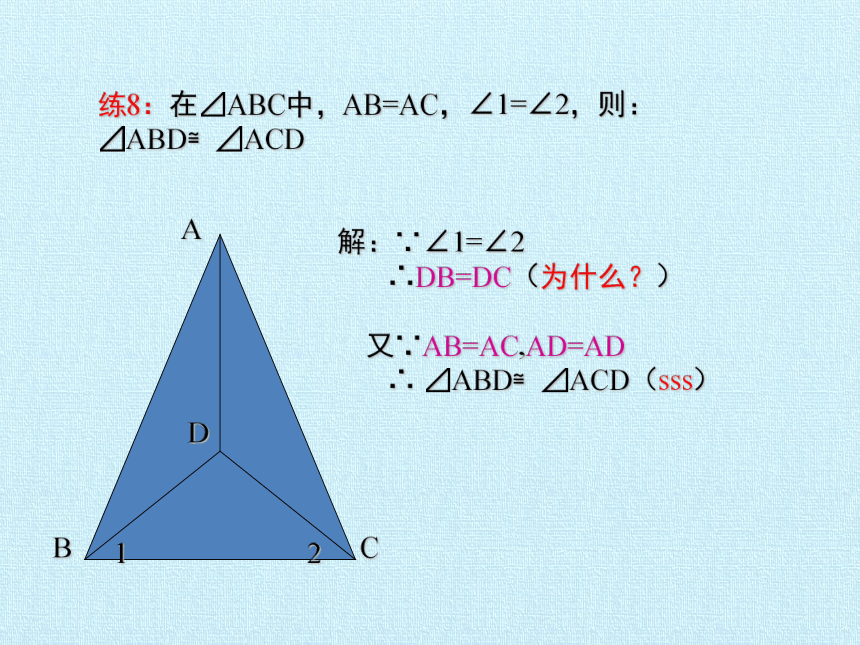
练8:在⊿ABC中,AB=AC,∠1=∠2,则:⊿ABD≌⊿ACD
2
1
D
C
B
A
解:∵∠1=∠2
∴DB=DC(为什么?)
又∵AB=AC,AD=AD
∴ ⊿ABD≌⊿ACD(sss)
5.三边都相等的三角形叫做等边三角形,也叫正三角形。等边三角形是特殊的等腰三角形,是腰和底边相等的等腰三角形。
6.等边三角形的性质:
a.三边相等
b.三个角相等,都是600
c.三线合一
d.轴对称图形,三条对称轴
7.说一说:
你用什么方法可以判定一个三角形是等边三角形?
8.有一个角是直角的三角形叫直角三角形。
9.直角三角形的两个锐角__________。
10.有两个角互余的三角形是直角三角形
11.两条直角边相等的直角三角形叫做等腰直角三角形,它的两个底角相等,都是450。
练9:在⊿ABC中,∠C=Rt∠,∠B=3∠A,求∠B和∠A的度数。
练10:在⊿ABC中,∠A:∠B:∠C=1:1:2,求三个内角的度数,并判断是什么三角形。
互余
12.直角三角形斜边上的中线等于___________。
13.若三角形中一边上的中线等于这条边的一半,那么这个三角形是___________。
练11:在Rt△ABC中,CD是斜边AB上的中线,若CD=3.5厘米,则AB=____厘米。
练12:在△BC中CD是AB边上的中线,且CD= AB,则△ABC是_________三角形。
1
2
—
斜边的一半
7
直角三角形
直角
14.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
15.勾股定理的逆定理:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
a
c
b
A
B
C
a
c
b
A
B
C
勾股定理的逆定理:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
勾股定理:
直角三角形两条直角边的平方和等于斜边的平方.
已知是RtΔ,得出边的关系
∵ΔABC是RtΔ
∴a2+b2=c2
∵a2+b2=c2
∴ΔABC是RtΔ
∠C是Rt∠
已知边的关系,判断出是RtΔ
练13:如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?
请写出并记忆常见的勾股数
A
D
C
B
练14:四边形ABCD中已知AB=3,BC=4,CD=12,DA=13,且∠ABC=900,求这个四边形的面积。
3
4
13
12
5
┌
12厘米或(7+√7)厘米
16.直角三角形全等的判定:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”)
17.角的内部,到角的两边距离相等的点,在这个角的平分线上。
B
A
C
D
E
F
练15:已知CE⊥AB,DF⊥AB,AC=BD,AF=BE,则CE=DF。请说明理由。
一、基础练习
1.在ΔABC中,如果∠A+∠B=∠C,且AC=1/2AB,则∠B=_______。
2.如图ΔABC中,∠ACB=90o,CD⊥AB,垂足是D,BC=5cm,BD=1/2BC,则AD=_______cm。
A
C
B
D
30o
7.5
3.如果等腰三角形底边上的高线等于腰长的一半,那么这个等腰三角形的三内角分别是_______________。
4.一艘轮船以16千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以12千米/时的速度向东南方向航行,那么它们离开港口1.5小时后,相距__________千米。
30o、30o、120o
30
7.如图,某校A与公路距离为3000米,又与该公路旁上的某车站D的距离为5000米,现要在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离约为( )
A.875米 B.3125米 C.3500米 D.3275米
C
D
A
5.如图,一个长为25分米的梯子,斜立在一竖直的墙上,
这时梯足距墙底端7分米,如果梯子的顶端沿墙下滑4分米。
那么梯足将滑( )
A.15分米B.9分米C.8分米D.5分米
6.如果等腰三角形底边上的高线等于腰长的一半,那么这个
等腰三角形的三个内角分别是( )
A.30°30°120°B.60°60°60°C.75°75°30°D.45°45°90°
C
A
A
思考:若A城与B地的方向保持不变,为了确保A城不受台风
影响至少离B地多远?
解:作AD ⊥ BF
∵由已知可得:
∠FBA=300
∴ AD=1/2AB=150KM
而 150<200
所以A城会受到台风的影响
二、应用与延伸
1.如图,设A城市气象台测得台风中心,在A城正西方向300千米的B处,正向北偏东600的BF方向移动,距台风中心200千米的范围内是受台风影响的区域,那么A城是否受到这次台风的影响?为什么?如果你是气象员,请你算一算。
东
北
F
B
A
600
D
2.如图,已知AB=AD,CB=CD,AC,BD相交于点O,若AB=5,
AC=7,BD=6,求∠BCD的度数。
解:∵AB=AD
∴点A在线段BD的中垂线上
同理点也在BD的中垂线上
∴AC⊥BD且平分BD
∵BD=6
∴BO=3
∵AB=5
由勾股定理得AO=4
∵AC=7
∴OC=3
∴△BOC等腰直角三角形
∴∠BCO=45°
同理∠DCO=45°
∴∠BCD=90°
A
B
D
C
O
3.如图,已知四边形ABCD中,∠B=90°,AB=4,BC=3,AD=12,DC=13,求四边形ABCD的面积。
A
B
C
D
解:连接AC
∵∠B=90°,AB=4,BC=3
∴AC=5
∵AD=12,DC=13
2
AC
2
AD
+
=
2
CD
∴∠CAD=90° S四边形ABCD=
×3×4+
×5×12=36
2
1
_
2
1
_
A
B
C
D
E
4.如图已知四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2,求
的值。
2
AB
2
1
_
解:延长AD、BC交于E
∵ ∠A=60°,∠B=∠D=90°
∵∠C=30°
CD=
CE,CD=2
∴CE=4,又BC=3
∴BE=7,由勾股定理得
∴AB=
2
1
_
AE,
2
AB
2
BE
+
=
2
AB
4
2
AB
=
49
—
3
谢 谢
第2章 特殊三角形
复习课件
特殊三角形
两个锐角互余
直角三角形斜边上的中线等于斜边的一半
勾股定理
直角三角形的性质
直角三角形的判定
两个直角三角形全等的判定方法:HL
有关角平分线的性质:角的内部,到角两边距离相等的点,在这个角的平分线上
等腰直角三角形
有两个角互余的三角形是直角三角形
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形
知识结构框架图
等边三角形
等腰三角形
等腰三角形的性质:轴对称性
等腰三角形的判定方法:在同一个三角形中,等角对等边
在同一个三角形中,等边对等角
底边上的高、中线、顶角平分线三线合一
直角三角形
等边三角形的性质和判定
1.什么是等腰三角形
有两边相等的三角形叫做等腰三角形
练1已知等腰三角形的两边长分别是4和6,则它的周长是________。
练2已知等腰三角形的两边长分别是3和6,则它的周长是________。
练3已知等腰三角形一腰上的中线将它的周长分成15cm和6cm两部分,则等腰三角形的底边长是__________。
14或16
15
1cm
2.等腰三角形是轴对称图形,它的对称轴是_________________________。
3.等腰三角形的两个底角相等。
A
C
B
∵
∴
AB=AC
∠B=∠C
(在同一个三角形中
等边对等角)
(已知)
顶角平分线所在的直线
练4:已知等腰三角形的一个底角是300,则它的顶角是__________。
练5:已知等腰三角形的一个角是300,则它的顶角是__________。
练6:已知等腰三角形的一个角是1300,则它的顶角是__________。
练7:已知等腰三角形的顶角是底角的2倍,则它的底角是__________。
1200
1200或300
1300
450
等腰三角形三线合一
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
用数学式子表示:
A
C
B
D
1
2
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
4.如果一个三角形有两个角相等,那么这个三角形是__________。
A
C
B
∵
∴
AB=AC
∠B=∠C
(在同一个三角形中
等角对等边)
(已知)
等腰三角形
练8:在⊿ABC中,AB=AC,∠1=∠2,则:⊿ABD≌⊿ACD
2
1
D
C
B
A
解:∵∠1=∠2
∴DB=DC(为什么?)
又∵AB=AC,AD=AD
∴ ⊿ABD≌⊿ACD(sss)
5.三边都相等的三角形叫做等边三角形,也叫正三角形。等边三角形是特殊的等腰三角形,是腰和底边相等的等腰三角形。
6.等边三角形的性质:
a.三边相等
b.三个角相等,都是600
c.三线合一
d.轴对称图形,三条对称轴
7.说一说:
你用什么方法可以判定一个三角形是等边三角形?
8.有一个角是直角的三角形叫直角三角形。
9.直角三角形的两个锐角__________。
10.有两个角互余的三角形是直角三角形
11.两条直角边相等的直角三角形叫做等腰直角三角形,它的两个底角相等,都是450。
练9:在⊿ABC中,∠C=Rt∠,∠B=3∠A,求∠B和∠A的度数。
练10:在⊿ABC中,∠A:∠B:∠C=1:1:2,求三个内角的度数,并判断是什么三角形。
互余
12.直角三角形斜边上的中线等于___________。
13.若三角形中一边上的中线等于这条边的一半,那么这个三角形是___________。
练11:在Rt△ABC中,CD是斜边AB上的中线,若CD=3.5厘米,则AB=____厘米。
练12:在△BC中CD是AB边上的中线,且CD= AB,则△ABC是_________三角形。
1
2
—
斜边的一半
7
直角三角形
直角
14.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
15.勾股定理的逆定理:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
a
c
b
A
B
C
a
c
b
A
B
C
勾股定理的逆定理:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
勾股定理:
直角三角形两条直角边的平方和等于斜边的平方.
已知是RtΔ,得出边的关系
∵ΔABC是RtΔ
∴a2+b2=c2
∵a2+b2=c2
∴ΔABC是RtΔ
∠C是Rt∠
已知边的关系,判断出是RtΔ
练13:如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?
请写出并记忆常见的勾股数
A
D
C
B
练14:四边形ABCD中已知AB=3,BC=4,CD=12,DA=13,且∠ABC=900,求这个四边形的面积。
3
4
13
12
5
┌
12厘米或(7+√7)厘米
16.直角三角形全等的判定:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”)
17.角的内部,到角的两边距离相等的点,在这个角的平分线上。
B
A
C
D
E
F
练15:已知CE⊥AB,DF⊥AB,AC=BD,AF=BE,则CE=DF。请说明理由。
一、基础练习
1.在ΔABC中,如果∠A+∠B=∠C,且AC=1/2AB,则∠B=_______。
2.如图ΔABC中,∠ACB=90o,CD⊥AB,垂足是D,BC=5cm,BD=1/2BC,则AD=_______cm。
A
C
B
D
30o
7.5
3.如果等腰三角形底边上的高线等于腰长的一半,那么这个等腰三角形的三内角分别是_______________。
4.一艘轮船以16千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以12千米/时的速度向东南方向航行,那么它们离开港口1.5小时后,相距__________千米。
30o、30o、120o
30
7.如图,某校A与公路距离为3000米,又与该公路旁上的某车站D的距离为5000米,现要在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离约为( )
A.875米 B.3125米 C.3500米 D.3275米
C
D
A
5.如图,一个长为25分米的梯子,斜立在一竖直的墙上,
这时梯足距墙底端7分米,如果梯子的顶端沿墙下滑4分米。
那么梯足将滑( )
A.15分米B.9分米C.8分米D.5分米
6.如果等腰三角形底边上的高线等于腰长的一半,那么这个
等腰三角形的三个内角分别是( )
A.30°30°120°B.60°60°60°C.75°75°30°D.45°45°90°
C
A
A
思考:若A城与B地的方向保持不变,为了确保A城不受台风
影响至少离B地多远?
解:作AD ⊥ BF
∵由已知可得:
∠FBA=300
∴ AD=1/2AB=150KM
而 150<200
所以A城会受到台风的影响
二、应用与延伸
1.如图,设A城市气象台测得台风中心,在A城正西方向300千米的B处,正向北偏东600的BF方向移动,距台风中心200千米的范围内是受台风影响的区域,那么A城是否受到这次台风的影响?为什么?如果你是气象员,请你算一算。
东
北
F
B
A
600
D
2.如图,已知AB=AD,CB=CD,AC,BD相交于点O,若AB=5,
AC=7,BD=6,求∠BCD的度数。
解:∵AB=AD
∴点A在线段BD的中垂线上
同理点也在BD的中垂线上
∴AC⊥BD且平分BD
∵BD=6
∴BO=3
∵AB=5
由勾股定理得AO=4
∵AC=7
∴OC=3
∴△BOC等腰直角三角形
∴∠BCO=45°
同理∠DCO=45°
∴∠BCD=90°
A
B
D
C
O
3.如图,已知四边形ABCD中,∠B=90°,AB=4,BC=3,AD=12,DC=13,求四边形ABCD的面积。
A
B
C
D
解:连接AC
∵∠B=90°,AB=4,BC=3
∴AC=5
∵AD=12,DC=13
2
AC
2
AD
+
=
2
CD
∴∠CAD=90° S四边形ABCD=
×3×4+
×5×12=36
2
1
_
2
1
_
A
B
C
D
E
4.如图已知四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2,求
的值。
2
AB
2
1
_
解:延长AD、BC交于E
∵ ∠A=60°,∠B=∠D=90°
∵∠C=30°
CD=
CE,CD=2
∴CE=4,又BC=3
∴BE=7,由勾股定理得
∴AB=
2
1
_
AE,
2
AB
2
BE
+
=
2
AB
4
2
AB
=
49
—
3
谢 谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
