浙教版数学八年级上册 第5章 一次函数 复习课课件 (共25张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 第5章 一次函数 复习课课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 977.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
复习目标
1.梳理本章知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
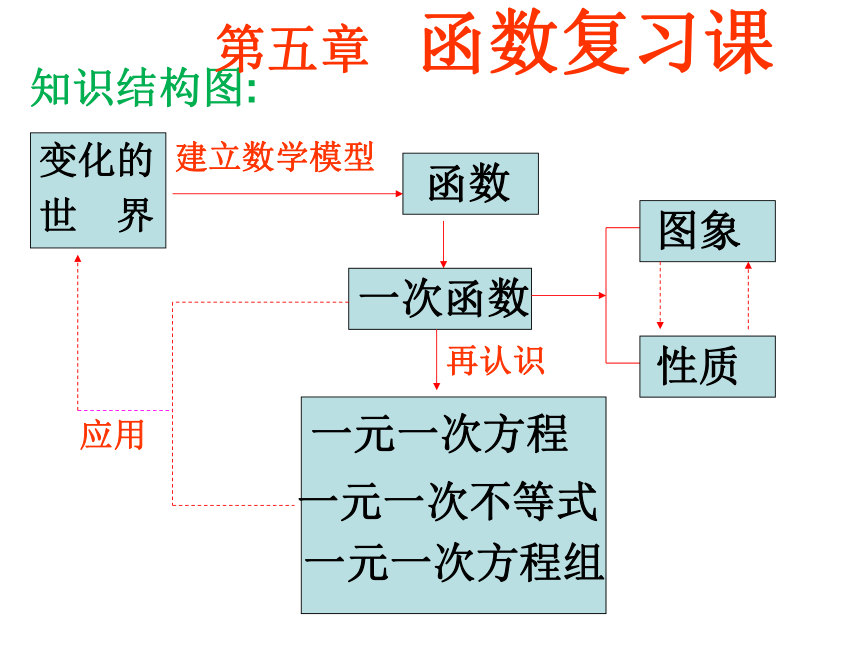
知识结构图:
变化的
世 界
函数
一次函数
图象
性质
一元一次方程
一元一次不等式
一元一次方程组
再认识
建立数学模型
应用
第五章 函数复习课
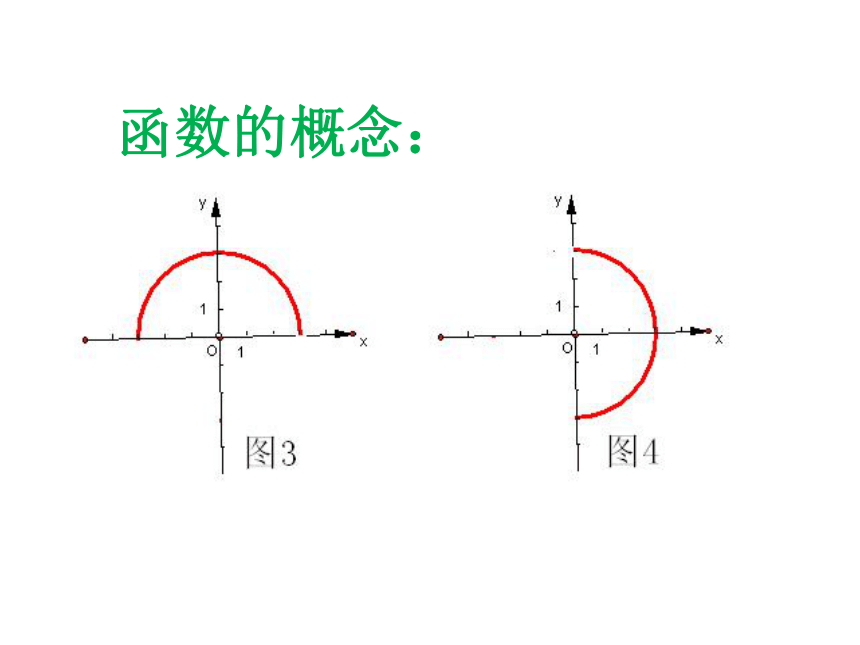
在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,
y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
函数的概念:
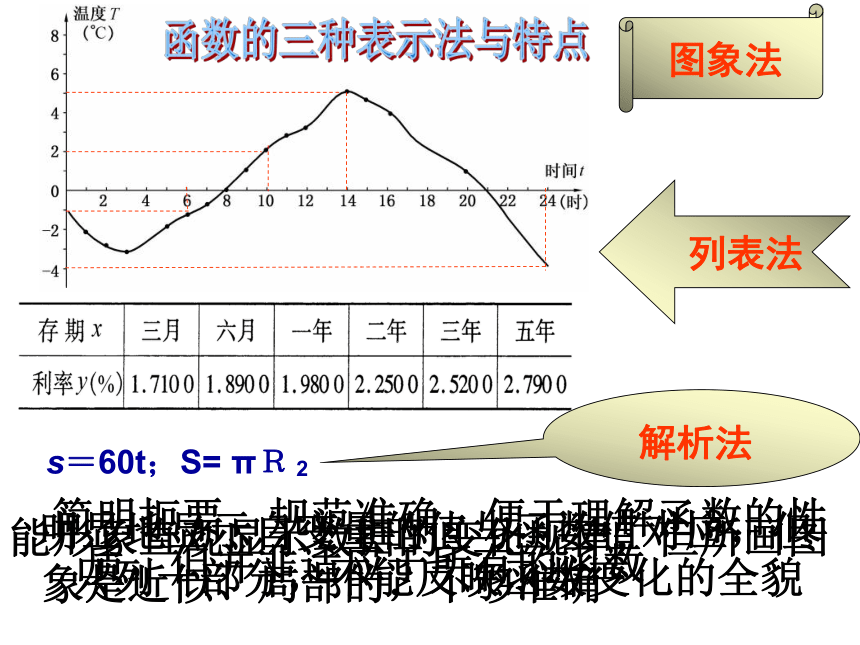
s=60t;S= πR
解析法
图象法
列表法
2
明显地显示自变量的值与函数值对应,但只列一部分,不能反映函数变化的全貌
能形象直观显示数据的变化规律,但所画图象是近似、局部的,不够准确
简明扼要、规范准确,便于理解函数的性质,但并非适应于所有的函数
八年级 数学
第十一章 函数
求出下列函数中自变量的取值范围
(3)
自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
八年级 数学
第十一章 函数
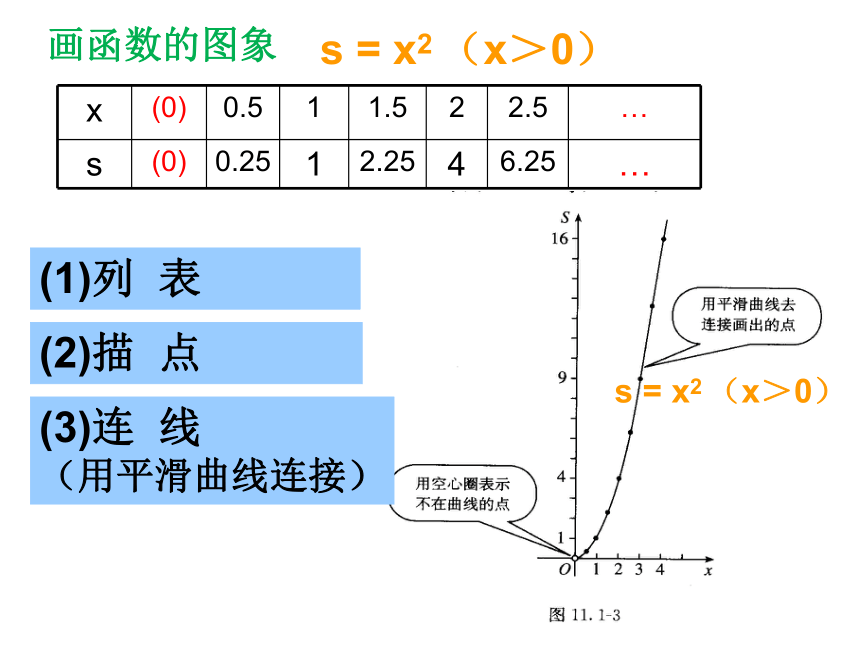
画函数的图象
x (0) 0.5 1 1.5 2 2.5 …
s (0) 0.25 1 2.25 4 6.25 …
s = x2 (x>0)
(2)描 点
(3)连 线
(用平滑曲线连接)
(1)列 表
s = x2 (x>0)
八年级 数学
第十一章 函数
一次函数的概念:
一般地,形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数.
当b =0 时,y=kx+b 即为 y=kx,
所以正比例函数,是一次函数的特例.
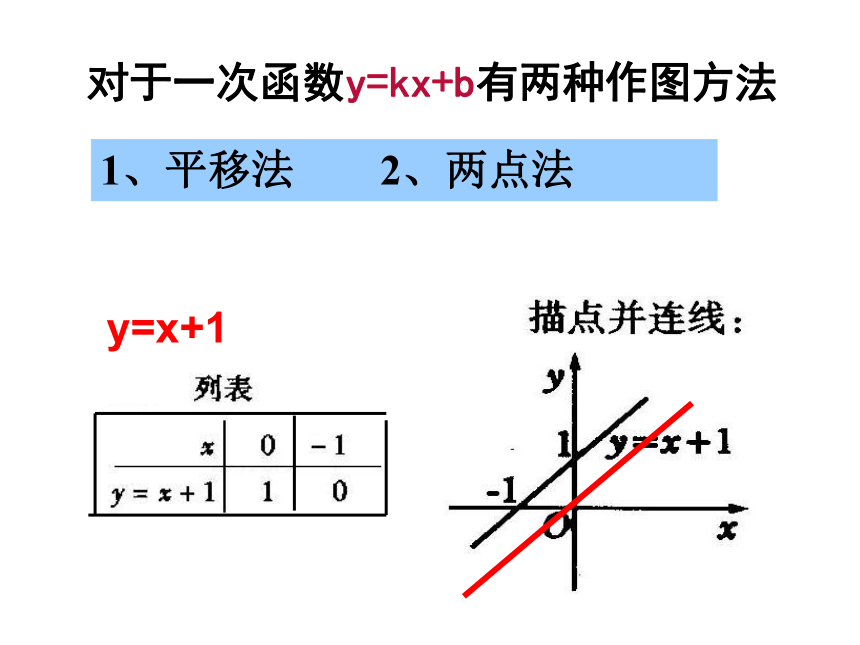
对于一次函数y=kx+b有两种作图方法
1、平移法 2、两点法
y=x+1
一次函数的图象与性质:
一次函数y=kx+b的图象是一条直线,
k>0, y随x的增大而增大;
k<0 ,y随x的增大而减小.
注意:k,b决定图象所经过的象限.
k决定上升与下降
b决定图象与y轴的交点位置.
与y轴的交点为 (0 , b )
与x轴的交点为 (-b/k , 0 )
y=kx+b (k、b是常数,且k≠0)
k>0 b > 0
b=0
b < 0
k<0 b > 0
b = 0
b < 0
一、二、三
一、 三
一、三、四
二、三、四
二、 四
一、二、四
直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx-k的图象只能是( )
B
1.若一次函数y=x+b的图象过点A(1,-1),则b=__________。
-2
2 .根据如图所示的条件,求直线的表达式。
与y轴的交点为 (0 , b )
与x轴的交点为 (-b/k , 0 )
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
求函数解析式的方法:
1.已知y+1与x-2成正比例,当x=3时,y=-3,
(1)求y与x的函数关系式;
(2)画出这个函数图象;
(3)求图象与坐标轴围成的三角形面积;
(4)当-1≤x≤4时,求y的取值范围;
注意点:
(1)函数表达形式要化简;
(2)第(4)小题解法:
①代数法
②图象法
知识点:
(1)正比例函数与一次函数的关系;
(2)一次函数图象的画法;
(3)一次函数图象与坐标轴交点坐标求法
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
A. B.
C. D.
P(1,1)
1
1
2
3
3
-1
O
2
y
x
-1
D
2.如图,已知函数y1=x+b和y2=ax+3的图象交于P点, 则x+b>ax+3不等式的解集为 .
O
x
y
1
P
y1=x+b
y2=ax+3
X>1
-1
3
当 y1>0且y2>0时,x的取值范围是_________
-11.如图,直线AB与y轴,x轴交点分别为A(0,2) B(4,0)
问题1:求直线AB的解析式
及△AOB的面积.
A
2
O
4
B
x
y
问题2:
当x满足什么条件时,y>0,y=0,y<0,0<y<2
当x<4时,y > 0,
当x=4时,y = 0,
当x >4时,y < 0,
当0< x<4时, 0< y <2,
A
2
O
4
B
x
y
问题3:
在x轴上是否存在一点P,使
若存在,请求出P点坐标,若不存在,请说明理由.
1
7
P
P
P(1,0)或(7,0)
问题4:若直线AB上有一点C,且点C的横坐标为0.4,求C的坐标及△AOC的面积.
A
2
O
4
B
x
y
0.4
C
问题5:若直线AB上有一点D,且点D的纵坐标为1.6,求D的坐标及直线OD的函数解析式.
A
2
O
4
B
x
y
1.6
D
C点的坐标(0.4,1.8)
D点的坐标(0.8,1.6)
y=2x
问题6:求直线AB上是否存在一点E,使点E到x轴的距离等于1.5,若存在求出点E的坐标,若不存在,请说明理由.
A
2
O
4
B
x
y
E
E
1.5
1.5
问题7:求直线AB上是否存在一点F,使点E到y轴的距离等0.6,若存在求出点F的坐标,若不存在,请说明理由.
E点的坐标(1,1.5)
或(7,-1.5)
F点的坐标(0.6,1.7)或(-0.6,2.3)
A
2
O
4
B
x
y
问题8:
在直线AB上是否存在一点G,使
若存在,请求出G点坐标,若不存在,请说明理由.
G
G
问题9:
已知x轴上点A(-4,0),B(2,0),若点C在一次函数 的图象上,且△ABC是直角三角形,则满足条件点C有( )
A.1个 B.2个 C.3个 D.4个
A
2
O
4
B
x
y
C
C
C
C
D
问题10: 如图,直线AB与y轴,x轴交点分别为A(0,2) B(4,0),以坐标轴上有一点C,使△ACB为等腰三角形
这样的点C有( )个
A.5个 B.6个 C.7个 D.8个
A
2
O
4
B
x
y
复习目标
1.梳理本章知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
知识结构图:
变化的
世 界
函数
一次函数
图象
性质
一元一次方程
一元一次不等式
一元一次方程组
再认识
建立数学模型
应用
第五章 函数复习课
在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,
y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
函数的概念:
s=60t;S= πR
解析法
图象法
列表法
2
明显地显示自变量的值与函数值对应,但只列一部分,不能反映函数变化的全貌
能形象直观显示数据的变化规律,但所画图象是近似、局部的,不够准确
简明扼要、规范准确,便于理解函数的性质,但并非适应于所有的函数
八年级 数学
第十一章 函数
求出下列函数中自变量的取值范围
(3)
自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
八年级 数学
第十一章 函数
画函数的图象
x (0) 0.5 1 1.5 2 2.5 …
s (0) 0.25 1 2.25 4 6.25 …
s = x2 (x>0)
(2)描 点
(3)连 线
(用平滑曲线连接)
(1)列 表
s = x2 (x>0)
八年级 数学
第十一章 函数
一次函数的概念:
一般地,形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数.
当b =0 时,y=kx+b 即为 y=kx,
所以正比例函数,是一次函数的特例.
对于一次函数y=kx+b有两种作图方法
1、平移法 2、两点法
y=x+1
一次函数的图象与性质:
一次函数y=kx+b的图象是一条直线,
k>0, y随x的增大而增大;
k<0 ,y随x的增大而减小.
注意:k,b决定图象所经过的象限.
k决定上升与下降
b决定图象与y轴的交点位置.
与y轴的交点为 (0 , b )
与x轴的交点为 (-b/k , 0 )
y=kx+b (k、b是常数,且k≠0)
k>0 b > 0
b=0
b < 0
k<0 b > 0
b = 0
b < 0
一、二、三
一、 三
一、三、四
二、三、四
二、 四
一、二、四
直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx-k的图象只能是( )
B
1.若一次函数y=x+b的图象过点A(1,-1),则b=__________。
-2
2 .根据如图所示的条件,求直线的表达式。
与y轴的交点为 (0 , b )
与x轴的交点为 (-b/k , 0 )
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
求函数解析式的方法:
1.已知y+1与x-2成正比例,当x=3时,y=-3,
(1)求y与x的函数关系式;
(2)画出这个函数图象;
(3)求图象与坐标轴围成的三角形面积;
(4)当-1≤x≤4时,求y的取值范围;
注意点:
(1)函数表达形式要化简;
(2)第(4)小题解法:
①代数法
②图象法
知识点:
(1)正比例函数与一次函数的关系;
(2)一次函数图象的画法;
(3)一次函数图象与坐标轴交点坐标求法
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
A. B.
C. D.
P(1,1)
1
1
2
3
3
-1
O
2
y
x
-1
D
2.如图,已知函数y1=x+b和y2=ax+3的图象交于P点, 则x+b>ax+3不等式的解集为 .
O
x
y
1
P
y1=x+b
y2=ax+3
X>1
-1
3
当 y1>0且y2>0时,x的取值范围是_________
-1
问题1:求直线AB的解析式
及△AOB的面积.
A
2
O
4
B
x
y
问题2:
当x满足什么条件时,y>0,y=0,y<0,0<y<2
当x<4时,y > 0,
当x=4时,y = 0,
当x >4时,y < 0,
当0< x<4时, 0< y <2,
A
2
O
4
B
x
y
问题3:
在x轴上是否存在一点P,使
若存在,请求出P点坐标,若不存在,请说明理由.
1
7
P
P
P(1,0)或(7,0)
问题4:若直线AB上有一点C,且点C的横坐标为0.4,求C的坐标及△AOC的面积.
A
2
O
4
B
x
y
0.4
C
问题5:若直线AB上有一点D,且点D的纵坐标为1.6,求D的坐标及直线OD的函数解析式.
A
2
O
4
B
x
y
1.6
D
C点的坐标(0.4,1.8)
D点的坐标(0.8,1.6)
y=2x
问题6:求直线AB上是否存在一点E,使点E到x轴的距离等于1.5,若存在求出点E的坐标,若不存在,请说明理由.
A
2
O
4
B
x
y
E
E
1.5
1.5
问题7:求直线AB上是否存在一点F,使点E到y轴的距离等0.6,若存在求出点F的坐标,若不存在,请说明理由.
E点的坐标(1,1.5)
或(7,-1.5)
F点的坐标(0.6,1.7)或(-0.6,2.3)
A
2
O
4
B
x
y
问题8:
在直线AB上是否存在一点G,使
若存在,请求出G点坐标,若不存在,请说明理由.
G
G
问题9:
已知x轴上点A(-4,0),B(2,0),若点C在一次函数 的图象上,且△ABC是直角三角形,则满足条件点C有( )
A.1个 B.2个 C.3个 D.4个
A
2
O
4
B
x
y
C
C
C
C
D
问题10: 如图,直线AB与y轴,x轴交点分别为A(0,2) B(4,0),以坐标轴上有一点C,使△ACB为等腰三角形
这样的点C有( )个
A.5个 B.6个 C.7个 D.8个
A
2
O
4
B
x
y
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
