浙教版数学七年级上册 第四章 代数式 复习课件(共36张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 第四章 代数式 复习课件(共36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-10 14:23:30 | ||
图片预览











文档简介
(共36张PPT)
第四章复习
(2) b÷a通常写作 ;
像 这样含有字母的数学表达式称为代数式。一个代数式由数、字母、运算符号组成.
(3) 数字通常写在字母前面;
(1) a×b通常写作a·b或ab;
如:a×3通常写作3a
(4) 带分数一般写成假分数.
如: 通常写作
代数式的规范写法:
{
规定: 单独一个数或一个字母也称代数式。
注意:代数式的书写格式要规范:
1.数和字母相乘时,省略乘号,并把数字写在字母的前面;
2.字母和字母相乘时,乘号可以省略不写 ;
3.除法运算写成分数形式;
4.“1”或“-1”和字母相乘时, 其中的“1”常省略不写;
5.带分数与字母相乘时,带分数要化成假分数的形式;
6.一个代数式就是一个整体,出现加减运算时,常用括号括起来;
用代数式表示:
x的 倍与3的差;
2a的立方根;
变式1:a与b的平方的和;
变式2:a、b两数的平方和.
大家一起来 式
列
a与b的和的平方.
变式: m的2倍除n所得的商
m的2倍除以n所得的商;
m的2倍除以n所得的商;
一般地,用数值代替代数式里的字母,计算后所得的结果,叫做代数式的值。
注意:代数式的值是由代数式里字母所取的值来确定的。
2、根据下列字母的不同取值,
求代数式 的值;
(1) x=-2, y=4;
(2)
试一试
单独一个数或一个字母也叫单项式,如:0,-1,a
由数与字母或字母与字母相乘组成的代数式叫做单项式。
分母不能带有字母。
根号里面不能带有字母。
代数式不能出现“+”“ —” 符号。
单项式定义:
-12 , -2a , , m ,
, -3x2+2y2-xy , ,
辨一辨
下列代数式中,哪些是单项式:
由数与字母或字母与字母相乘组成的代数式叫做单项式.
单独一个数或一个字母也叫单项式.
,
,
,
,
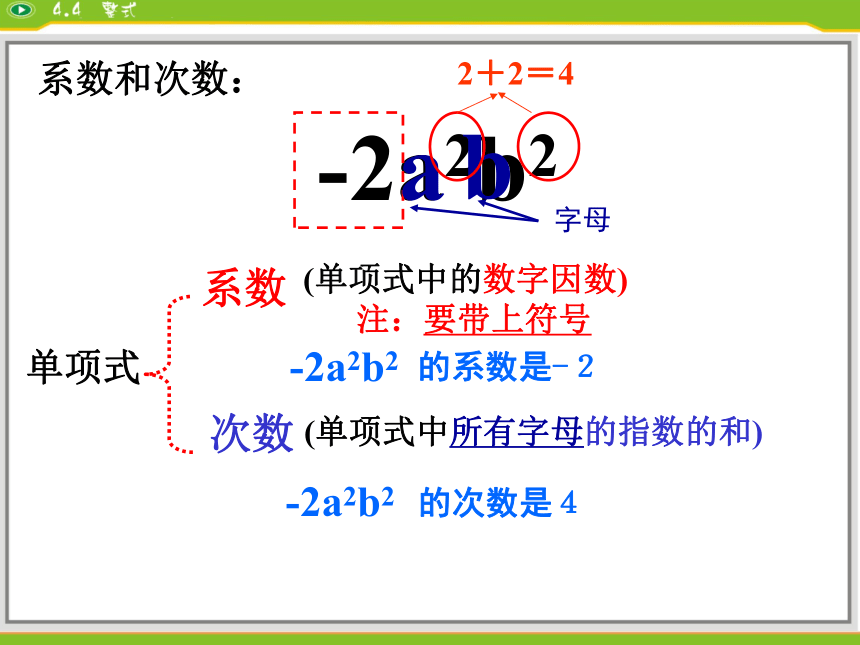
-2a2b2
单项式
系数
次数
(单项式中的数字因数)
注:要带上符号
(单项式中所有字母的指数的和)
-2a2b2
的系数是-2
-2a2b2
的次数是4
字母
a
b
2+2=4
系数和次数:
研究单项式的系数和次数:
单项式
系数
次数
1
1
注意:单独一个数字,系数就是它本身,次数为零
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
(注意:要连同数字前面的符号)
先确定有几个字母,再确定每个字母的指数,最后相加
-3x + 2a2 - ab2 +5
每个单项式叫做多项式的项(包括符号)。
不含字母的项叫做常数项。
次数最高的项的次数就是这个多项式的次数。
-3x
2a2
- ab2
5
在多项式中,
(三次多项式)
+
+
+
(-3x + 2a2 - ab2 +5的项有
-3x,
2a2
,-ab2
,5)
(-3x + 2a2 - ab2 +5的常数项是
5)
1
2
3
0
(次数最高的项 的次数是3)
-ab2
(三次四项式)
多项式:
项数:多少项
比较单项式的次数和多项式的次数的区别:
1、单项式中所有字母的指数的和叫做这个单项式的次数。
2、组成多项式的几个单项式里,次数最高的单项式的次数就是这个多项式的次数。
单项式、多项式统称为整式
多项式 项数 项的组成 常数项 次数
-3x+4y
a2+3a-2
a2-b3+3
2
3
3
-3x
, 4y
1
无
2
3
-2
3
a2
, 3a
, -2
a2
, -b3
, 3
轻松过关
1.下列说法正确的是: ( )
A. 不是单项式;
B. 是单项式;
C.x2y是二次单项式; D.-abc的系数是-1.
2.若xn+2y2z是一个七次单项式,则n的值是( )
A.0 B.1 C.2 D.3
3.下列代数式中不是整式的是( )
A.3x2+2x-1
B.
C.
D.
4. xy的系数是_______,次数是________.
5.写出2个含有两个字母a,b,并且系数为-2的3次
单项式_________.
6.多项式7x2-2xy+3y2+4是___次多项式.
7.下列代数式中,哪些是整式?哪些是单项式?哪些
是多项式?把它们填在相应的横线上:
属于整式的有:___________________________ ;
属于单项式的有:___________________________;
属于多项式的有:___________________________.
若 是关于x,y的一个单项式,且其系数为3,次数为4,则mn的值为( )
A.9
B.-9
C.12
D.-12
4. 如果多项式x2-7x-2和3x2+5x+n的常
数项相同,则n - =_______。
5. 当m=______时,多项式
8x2+3mxy-5y2+ xy-8中不含xy项。
思考
已知代数式3xn-(m-1)x+1是关于x的三次三项式,求m、n的条件。
已知:3xmy2m-1z- x2y-4是一个六次多项式,求m的值。
2.同类项与系数大小无关;
3.同类项与它们所含相同字母的顺序无关;
议一议
怎样判断同类项?
1. 同类项有两个标准
(1)所含字母相同;
(2)相同字母的指数分别相同;
★所含字母要相同;
★相同字母的指数也要相同.
★与字母顺序无关;
★与系数无关.
定义:多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
★要注意:所有常数项也看做同类项.
所有常数项也看做同类项.
辨一辨:
下列各组中的两项是不是同类项?为什么?
不是
不是
是
是
不是
2、 与 是同类项, 与 是同类项.
例1 指出下列多项式中的同类项:
1、3x-2y+1+3y-2x-5;
解 :1、3x与-2x是同类项,-2y与3y是同类项,1与-5是同类项.
例1 指出下列多项式中的同类项:
1、3x-2y+1+3y-2x-5;
(1)、如果 是同类项,那么 。
(2)、如果 是同类项,那么 , 。
2
4
3
练一练
合并同类项
把多项式中的同类项合并成一项叫做合并同类项
法
则
①把同类项的系数相加,所得的
结果作为新的系数;
②字母以及字母的指数不变。
一变
一不变
(1)、
(2)、
(3)、
(4)、
辨一辨
(5) a2-(2a-b+c)=a2-2a-b+c
(6)-2(x-y)-(y-1)=-2x-y+y-1.
先化简,再求值:
(1)
其中
(2)
其中
去括号前后,括号里各项的符号有什么变化?
去括号法则
(1)2(1-3x) =
(2)-(x2-3x) =
(3)-3(2x2-1)=
去括号:
2-6x
-x2+3x
-6x2 +3
(4)-2( x-y)=
(5)-0.5( 1 -2c)=
-x +2y
-0.5 +c
1.
2.
(
)
[
]
xy
x
xy
y
y
xy
ba
a
b
ab
b
a
2
5
2
3
2
2
3
3
2
5
2
2
2
2
2
2
2
+
+
-
-
-
-
-
+
-
-
)
(
)
(
)
(
3.
算一算
3:如果x无论取何值,代数式
的值总是3,试求m、n的值。
4:代数式
与
的和是
A:奇数
B:偶数
C: 5的倍数
D:以上都不能确定
已知A=a-2b+1,B=-3a+2b-2,
当a=22/7,b=-7时.
求整式3x+4y与2x-2y-1的和.
变式1:求整式3x+4y与2x-2y-1的差.
问题1:
变式2: 设 A= 3x+4y B= 2x-2y-1
求
问题2:
注意:去多重括号,有两种方法:
1.由内向外 2.由外向内?
去多重括号
变式2: 设 A= 3x+4y B= 2x-2y-1
求
求x=1,y=-1时,求 的值
求一求:
题组训练
求k为何值时,关于x,y的代数式
x6 -5kx4y3 - 4x6 +x4y3 +10中,
不含 x4y3 的项。
-5kx4y3
+x4y3
问题3:
求k为何值时,关于x,y的代数式
x2 -kxy+10 +xy 中, 不含xy 的项。
-kxy
+xy
a
自主
已知A=-3x2-2x+1,B=6x2+4x-1,
试说明:2A+B的值与x无关,
问题4:
变式1:已知A=mx2-2x+1(关于x的代数式),
B=6x2+4x-1,
且2A+B的值与x无关,求m的值
变式2:已知A= mx2-2x+1,
B=6x2+nx-1,
无论x取何值,2A+B的值总是1.
(与x的取值无关)
求m,n的值
(A,B是关于x的代数式)
第四章复习
(2) b÷a通常写作 ;
像 这样含有字母的数学表达式称为代数式。一个代数式由数、字母、运算符号组成.
(3) 数字通常写在字母前面;
(1) a×b通常写作a·b或ab;
如:a×3通常写作3a
(4) 带分数一般写成假分数.
如: 通常写作
代数式的规范写法:
{
规定: 单独一个数或一个字母也称代数式。
注意:代数式的书写格式要规范:
1.数和字母相乘时,省略乘号,并把数字写在字母的前面;
2.字母和字母相乘时,乘号可以省略不写 ;
3.除法运算写成分数形式;
4.“1”或“-1”和字母相乘时, 其中的“1”常省略不写;
5.带分数与字母相乘时,带分数要化成假分数的形式;
6.一个代数式就是一个整体,出现加减运算时,常用括号括起来;
用代数式表示:
x的 倍与3的差;
2a的立方根;
变式1:a与b的平方的和;
变式2:a、b两数的平方和.
大家一起来 式
列
a与b的和的平方.
变式: m的2倍除n所得的商
m的2倍除以n所得的商;
m的2倍除以n所得的商;
一般地,用数值代替代数式里的字母,计算后所得的结果,叫做代数式的值。
注意:代数式的值是由代数式里字母所取的值来确定的。
2、根据下列字母的不同取值,
求代数式 的值;
(1) x=-2, y=4;
(2)
试一试
单独一个数或一个字母也叫单项式,如:0,-1,a
由数与字母或字母与字母相乘组成的代数式叫做单项式。
分母不能带有字母。
根号里面不能带有字母。
代数式不能出现“+”“ —” 符号。
单项式定义:
-12 , -2a , , m ,
, -3x2+2y2-xy , ,
辨一辨
下列代数式中,哪些是单项式:
由数与字母或字母与字母相乘组成的代数式叫做单项式.
单独一个数或一个字母也叫单项式.
,
,
,
,
-2a2b2
单项式
系数
次数
(单项式中的数字因数)
注:要带上符号
(单项式中所有字母的指数的和)
-2a2b2
的系数是-2
-2a2b2
的次数是4
字母
a
b
2+2=4
系数和次数:
研究单项式的系数和次数:
单项式
系数
次数
1
1
注意:单独一个数字,系数就是它本身,次数为零
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
(注意:要连同数字前面的符号)
先确定有几个字母,再确定每个字母的指数,最后相加
-3x + 2a2 - ab2 +5
每个单项式叫做多项式的项(包括符号)。
不含字母的项叫做常数项。
次数最高的项的次数就是这个多项式的次数。
-3x
2a2
- ab2
5
在多项式中,
(三次多项式)
+
+
+
(-3x + 2a2 - ab2 +5的项有
-3x,
2a2
,-ab2
,5)
(-3x + 2a2 - ab2 +5的常数项是
5)
1
2
3
0
(次数最高的项 的次数是3)
-ab2
(三次四项式)
多项式:
项数:多少项
比较单项式的次数和多项式的次数的区别:
1、单项式中所有字母的指数的和叫做这个单项式的次数。
2、组成多项式的几个单项式里,次数最高的单项式的次数就是这个多项式的次数。
单项式、多项式统称为整式
多项式 项数 项的组成 常数项 次数
-3x+4y
a2+3a-2
a2-b3+3
2
3
3
-3x
, 4y
1
无
2
3
-2
3
a2
, 3a
, -2
a2
, -b3
, 3
轻松过关
1.下列说法正确的是: ( )
A. 不是单项式;
B. 是单项式;
C.x2y是二次单项式; D.-abc的系数是-1.
2.若xn+2y2z是一个七次单项式,则n的值是( )
A.0 B.1 C.2 D.3
3.下列代数式中不是整式的是( )
A.3x2+2x-1
B.
C.
D.
4. xy的系数是_______,次数是________.
5.写出2个含有两个字母a,b,并且系数为-2的3次
单项式_________.
6.多项式7x2-2xy+3y2+4是___次多项式.
7.下列代数式中,哪些是整式?哪些是单项式?哪些
是多项式?把它们填在相应的横线上:
属于整式的有:___________________________ ;
属于单项式的有:___________________________;
属于多项式的有:___________________________.
若 是关于x,y的一个单项式,且其系数为3,次数为4,则mn的值为( )
A.9
B.-9
C.12
D.-12
4. 如果多项式x2-7x-2和3x2+5x+n的常
数项相同,则n - =_______。
5. 当m=______时,多项式
8x2+3mxy-5y2+ xy-8中不含xy项。
思考
已知代数式3xn-(m-1)x+1是关于x的三次三项式,求m、n的条件。
已知:3xmy2m-1z- x2y-4是一个六次多项式,求m的值。
2.同类项与系数大小无关;
3.同类项与它们所含相同字母的顺序无关;
议一议
怎样判断同类项?
1. 同类项有两个标准
(1)所含字母相同;
(2)相同字母的指数分别相同;
★所含字母要相同;
★相同字母的指数也要相同.
★与字母顺序无关;
★与系数无关.
定义:多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
★要注意:所有常数项也看做同类项.
所有常数项也看做同类项.
辨一辨:
下列各组中的两项是不是同类项?为什么?
不是
不是
是
是
不是
2、 与 是同类项, 与 是同类项.
例1 指出下列多项式中的同类项:
1、3x-2y+1+3y-2x-5;
解 :1、3x与-2x是同类项,-2y与3y是同类项,1与-5是同类项.
例1 指出下列多项式中的同类项:
1、3x-2y+1+3y-2x-5;
(1)、如果 是同类项,那么 。
(2)、如果 是同类项,那么 , 。
2
4
3
练一练
合并同类项
把多项式中的同类项合并成一项叫做合并同类项
法
则
①把同类项的系数相加,所得的
结果作为新的系数;
②字母以及字母的指数不变。
一变
一不变
(1)、
(2)、
(3)、
(4)、
辨一辨
(5) a2-(2a-b+c)=a2-2a-b+c
(6)-2(x-y)-(y-1)=-2x-y+y-1.
先化简,再求值:
(1)
其中
(2)
其中
去括号前后,括号里各项的符号有什么变化?
去括号法则
(1)2(1-3x) =
(2)-(x2-3x) =
(3)-3(2x2-1)=
去括号:
2-6x
-x2+3x
-6x2 +3
(4)-2( x-y)=
(5)-0.5( 1 -2c)=
-x +2y
-0.5 +c
1.
2.
(
)
[
]
xy
x
xy
y
y
xy
ba
a
b
ab
b
a
2
5
2
3
2
2
3
3
2
5
2
2
2
2
2
2
2
+
+
-
-
-
-
-
+
-
-
)
(
)
(
)
(
3.
算一算
3:如果x无论取何值,代数式
的值总是3,试求m、n的值。
4:代数式
与
的和是
A:奇数
B:偶数
C: 5的倍数
D:以上都不能确定
已知A=a-2b+1,B=-3a+2b-2,
当a=22/7,b=-7时.
求整式3x+4y与2x-2y-1的和.
变式1:求整式3x+4y与2x-2y-1的差.
问题1:
变式2: 设 A= 3x+4y B= 2x-2y-1
求
问题2:
注意:去多重括号,有两种方法:
1.由内向外 2.由外向内?
去多重括号
变式2: 设 A= 3x+4y B= 2x-2y-1
求
求x=1,y=-1时,求 的值
求一求:
题组训练
求k为何值时,关于x,y的代数式
x6 -5kx4y3 - 4x6 +x4y3 +10中,
不含 x4y3 的项。
-5kx4y3
+x4y3
问题3:
求k为何值时,关于x,y的代数式
x2 -kxy+10 +xy 中, 不含xy 的项。
-kxy
+xy
a
自主
已知A=-3x2-2x+1,B=6x2+4x-1,
试说明:2A+B的值与x无关,
问题4:
变式1:已知A=mx2-2x+1(关于x的代数式),
B=6x2+4x-1,
且2A+B的值与x无关,求m的值
变式2:已知A= mx2-2x+1,
B=6x2+nx-1,
无论x取何值,2A+B的值总是1.
(与x的取值无关)
求m,n的值
(A,B是关于x的代数式)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
