2.2二次函数的图象（2）

(共16张PPT)
课程标准浙教版实验教科书
九年级 上 册
知识回顾:
二次函数y=ax 的图象及其特点？
1、顶点坐标？
（0，0）
2、对称轴？
y轴（直线x=0）
3、图象具有以下特点：
一般地，二次函数y=ax （ a≠0 ）的图象是一条抛物线；
当a>0 时，抛物线开口向上，顶点是抛物线上的最低点；
抛物线在x轴的上方（除顶点外）。
当a<0 时，抛物线开口向下，顶点是抛物线上的最高点。
抛物线在x轴的下方（除顶点外）
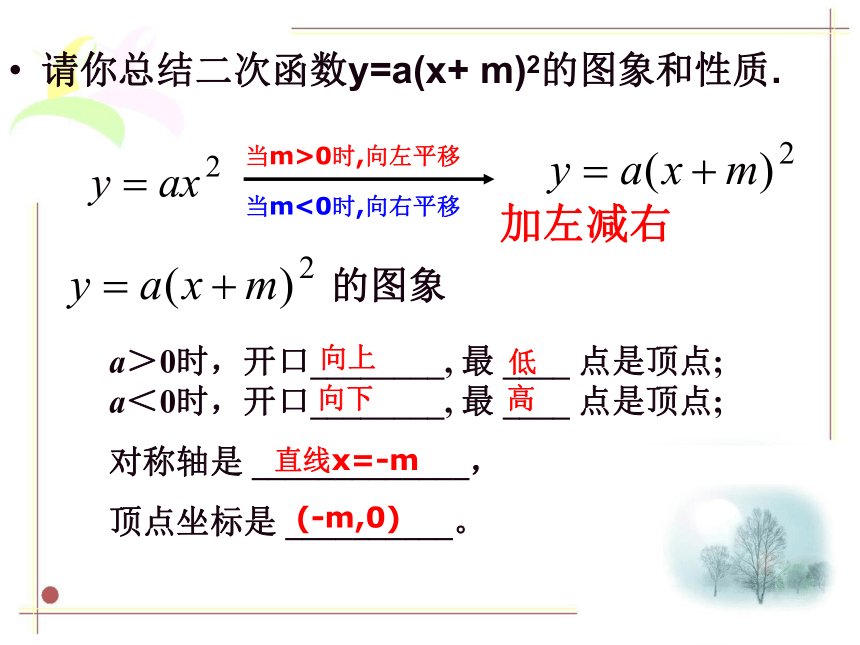
请你总结二次函数y=a(x+ m)2的图象和性质.
当m>0时,向左平移
当m<0时,向右平移
a＞0时，开口________, 最 ____ 点是顶点; a＜0时，开口________, 最 ____ 点是顶点;
对称轴是 _____________，
顶点坐标是 __________。
直线x=-m
(-m,0)
的图象
向上
向下
低
高
加左减右
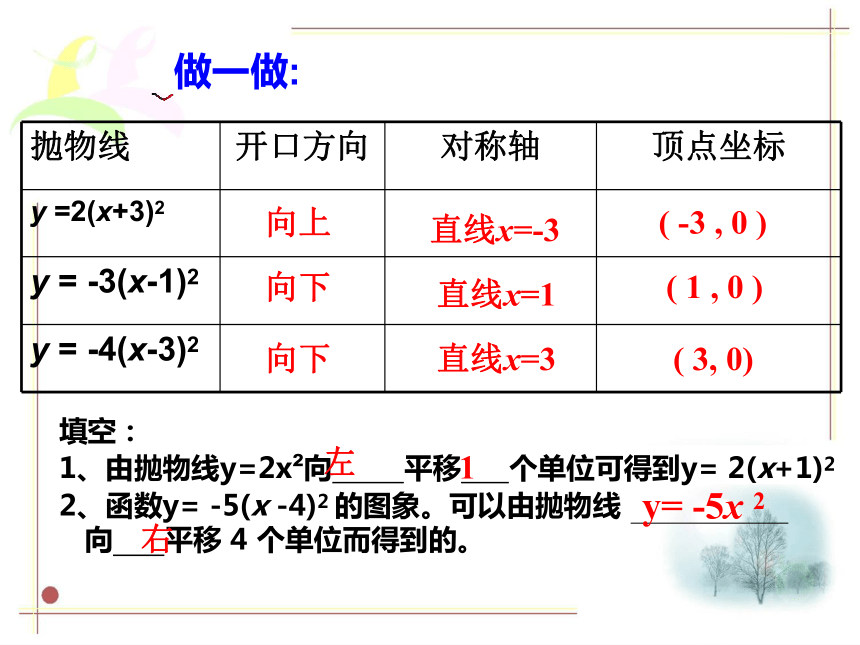
做一做:
抛物线 开口方向 对称轴 顶点坐标
y =2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
( -3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
填空：
1、由抛物线y=2x 向 平移 个单位可得到y= 2(x+1)2
2、函数y= -5(x -4)2 的图象。可以由抛物线
向 平移 4 个单位而得到的。
左
1
y= -5x 2
右
讨论归纳:
当m>0时,向左平移
当m<0时,向右平移
当k>０时向上平移
当k<０时向下平移
顶点坐标：
（０，０）
（-m,0)
(-m,k)
的图象：
对称轴是 _____________，
顶点坐标是 __________。
直线x=-m
(-m, k)
加左减右
正上负下
概括函数
的性质
开口方向、对称轴和顶点坐标
1、指出下列二次函数的开口方向、对称轴和顶点坐标：
课内练习:
填空：
1、由抛物线y=2x 向 平移 个单位,
再向 平移 个单位可得到y= 2(x +1)2 –3。
2、函数y= 3(x - 2)2 + 的图象。
可以由抛物线 向 平移 个单位，
再向 平移 个单位而得到的。
做一做:
1、 如果抛物线 的顶点坐标
是（-1，5）则 ;
它的对称轴是 .
２、 如果一条抛物线的形状与
的形状相同，且顶点坐标是（４，-２）则函数
关系式是 .
1、把抛物线 向上平移3个单位，向右平移3个单位得到的抛物线是 ；
2、把抛物线 向___平移___个单位，向___平移___个单位得到的抛物线 ；
5.
1、已知二次函数
的图象如图所示，则函数
的图象只可能是（ ）
2、
＞
＜
＜
＜
=
＞
＞
＞
＞
6、
在直角坐标平面内，二次函数图象的顶点为
（1，-4）。且过点B（3，0）。
（1）求该二次函数的解析式；
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x轴的另一个交点的坐标。