解直角三角形应用复习课
图片预览



文档简介
(共22张PPT)
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,你能根据这些条件求出南峰塔的高度吗
1、在Rt△ABC中,∠C=900,a,b,c分别是∠A,∠B,
∠C的对边.
(1)已知a=3,b=3,求∠A;
(2)已知c=8,b=4,求a及∠A;
(3)已知c=8,∠A=450,求a及b
A
B
C
a
b
c
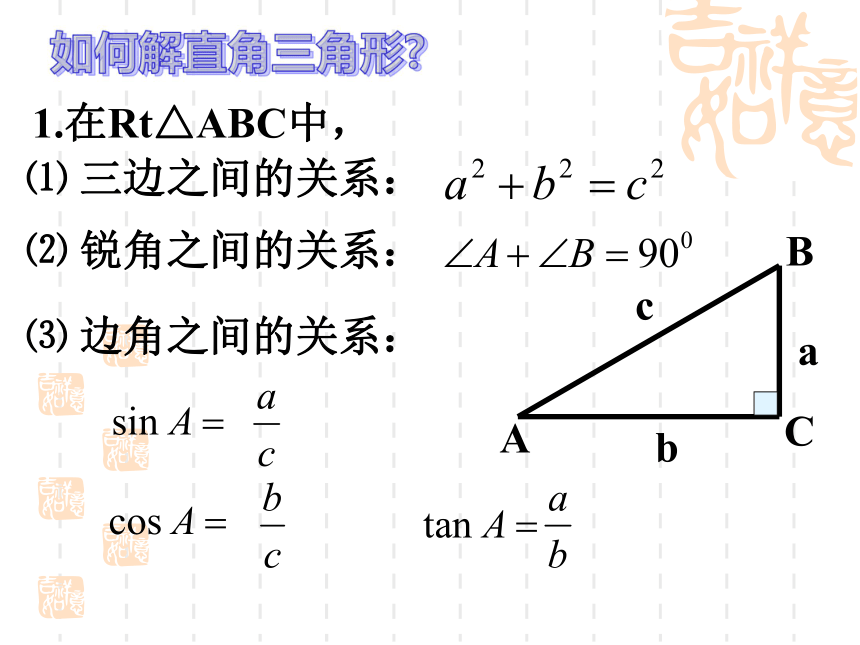
1.在Rt△ABC中,
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
1.某人沿坡度为i= 1: 的山路行了20m,则该人升高了_____
l
h
α
1.坡度
tan α =
h
l
α为坡角
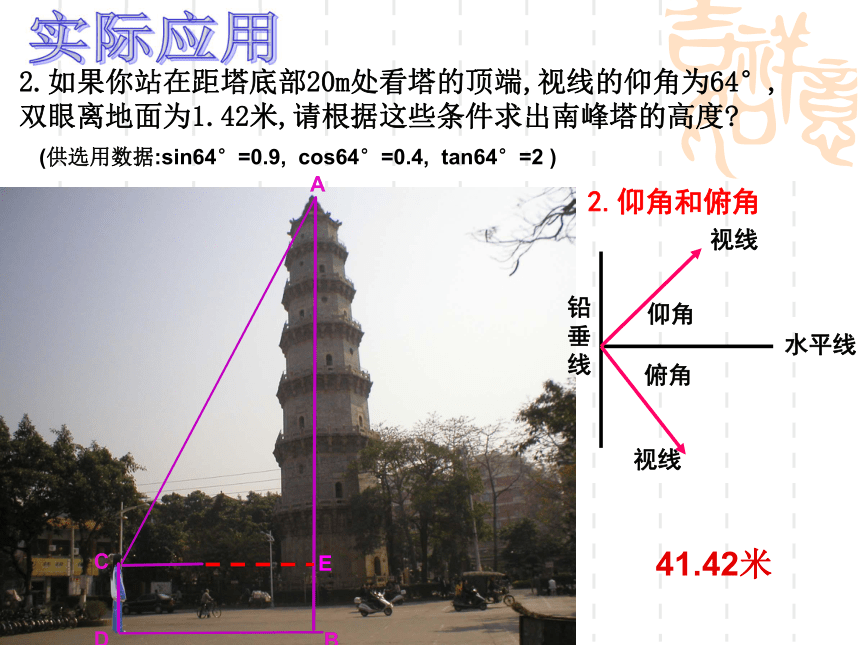
2.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,请根据这些条件求出南峰塔的高度
A
B
C
D
(供选用数据:sin64°=0.9, cos64°=0.4, tan64°=2 )
2.仰角和俯角
E
视线
铅垂线
水平线
视线
仰角
俯角
41.42米
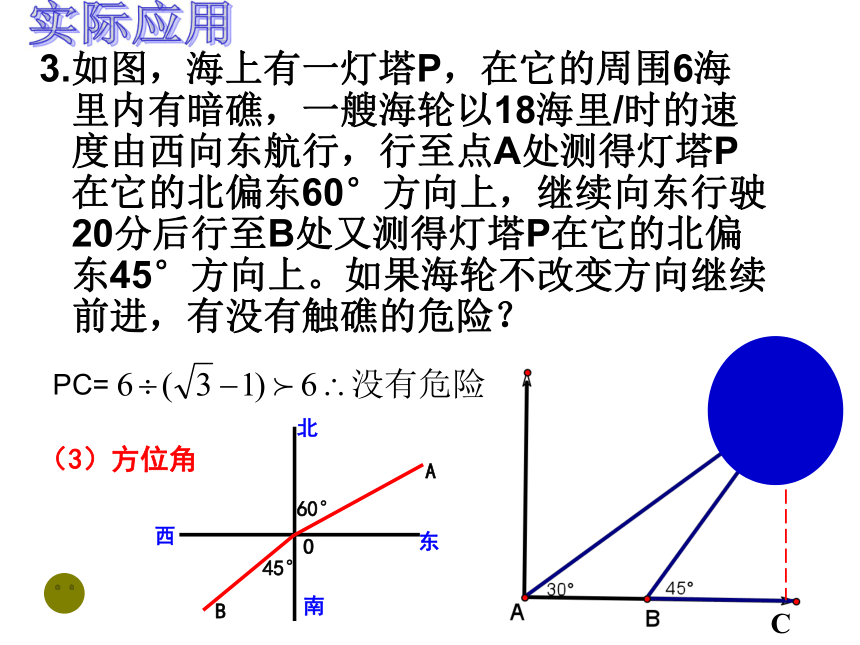
3.如图,海上有一灯塔P,在它的周围6海里内有暗礁,一艘海轮以18海里/时的速度由西向东航行,行至点A处测得灯塔P在它的北偏东60°方向上,继续向东行驶20分后行至B处又测得灯塔P在它的北偏东45°方向上。如果海轮不改变方向继续前进,有没有触礁的危险?
(3)方位角
60°
45°
B
O
A
东
西
北
南
C
PC=
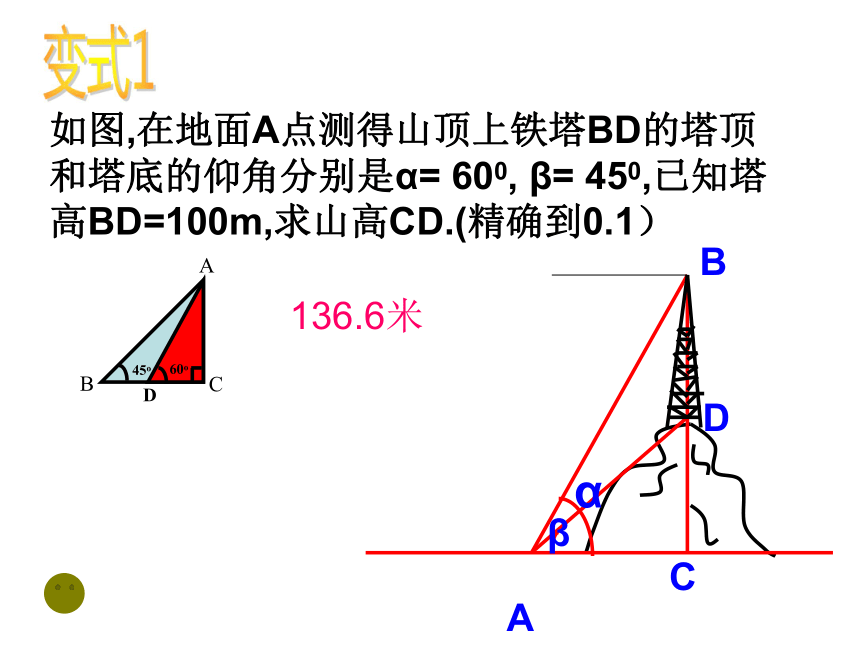
如图,在地面A点测得山顶上铁塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知塔高BD=100m,求山高CD.(精确到0.1)
A
B
C
D
α
β
45o
C
A
B
60o
D
136.6米
45o
C
A
B
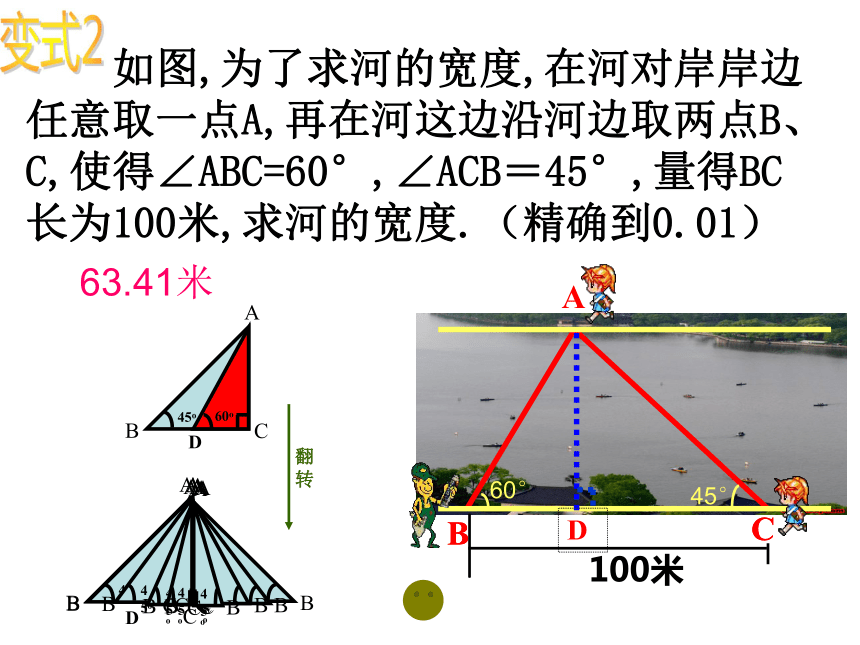
如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度.(精确到0.01)
D
60°
45°
A
B
C
B
C
100米
D
B
C
A
45o
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
63.41米
B
D
A
C
E
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
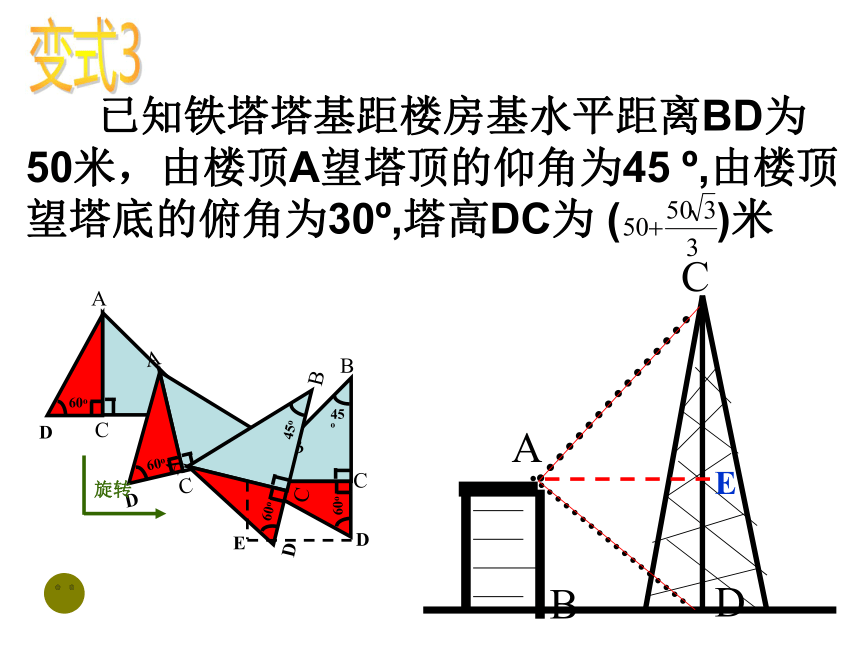
已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 ,由楼顶望塔底的俯角为30 ,塔高DC为 ( )米
45o
A
B
C
45o
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
问题1楼房AB的高度是多少
问题2楼房CD的高度是多少
50m
B
45
A
E
30
D
C
50米
已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.
A
B
C
D
F
E
B
C
A
45o
60o
D
1、通过以上习题学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
2、注意可解直角三角形与非可解直角三角形的基本解题思路;
A
A
B
B
C
C
D
D
3、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
有无解?
自我超越
一架25米长的梯子斜靠在墙上,梯子的底部离墙脚7米,如果梯子的顶部滑下4米,梯子的底部滑开多远?
解
如图,根据题意知
AB=25,BE=7,AC=4
在Rt△ABE中,AE 2=AB2-BE2
在Rt△CDE中,DE 2=CD2-CE2
AE=√252-72= 24
DE=√ 252 –202=15
所以BD=DE–BE=15–7=8(米)
A
D
C
B
E
答:梯子的底部滑开8米
∴CE=20
已知:AB=25,BE=7,
AC=4. 求BD的长度.
楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
现在你能完成这个任务吗
A
B
C
D
┌
联想的功能
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长, (2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
联想的功能
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
钢缆长几何
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CB上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
怎么做
我先将它数学化!
E
B
C
D
2m
400
5m
真知在实践中诞生
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.
求DE的长.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
单元知识网络
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
实际应用
画图,找直角三角形,利用三角函数
解直角三角形
A
C
B
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,你能根据这些条件求出南峰塔的高度吗
1、在Rt△ABC中,∠C=900,a,b,c分别是∠A,∠B,
∠C的对边.
(1)已知a=3,b=3,求∠A;
(2)已知c=8,b=4,求a及∠A;
(3)已知c=8,∠A=450,求a及b
A
B
C
a
b
c
1.在Rt△ABC中,
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
1.某人沿坡度为i= 1: 的山路行了20m,则该人升高了_____
l
h
α
1.坡度
tan α =
h
l
α为坡角
2.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,请根据这些条件求出南峰塔的高度
A
B
C
D
(供选用数据:sin64°=0.9, cos64°=0.4, tan64°=2 )
2.仰角和俯角
E
视线
铅垂线
水平线
视线
仰角
俯角
41.42米
3.如图,海上有一灯塔P,在它的周围6海里内有暗礁,一艘海轮以18海里/时的速度由西向东航行,行至点A处测得灯塔P在它的北偏东60°方向上,继续向东行驶20分后行至B处又测得灯塔P在它的北偏东45°方向上。如果海轮不改变方向继续前进,有没有触礁的危险?
(3)方位角
60°
45°
B
O
A
东
西
北
南
C
PC=
如图,在地面A点测得山顶上铁塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知塔高BD=100m,求山高CD.(精确到0.1)
A
B
C
D
α
β
45o
C
A
B
60o
D
136.6米
45o
C
A
B
如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度.(精确到0.01)
D
60°
45°
A
B
C
B
C
100米
D
B
C
A
45o
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
63.41米
B
D
A
C
E
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 ,由楼顶望塔底的俯角为30 ,塔高DC为 ( )米
45o
A
B
C
45o
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
问题1楼房AB的高度是多少
问题2楼房CD的高度是多少
50m
B
45
A
E
30
D
C
50米
已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.
A
B
C
D
F
E
B
C
A
45o
60o
D
1、通过以上习题学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
2、注意可解直角三角形与非可解直角三角形的基本解题思路;
A
A
B
B
C
C
D
D
3、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
有无解?
自我超越
一架25米长的梯子斜靠在墙上,梯子的底部离墙脚7米,如果梯子的顶部滑下4米,梯子的底部滑开多远?
解
如图,根据题意知
AB=25,BE=7,AC=4
在Rt△ABE中,AE 2=AB2-BE2
在Rt△CDE中,DE 2=CD2-CE2
AE=√252-72= 24
DE=√ 252 –202=15
所以BD=DE–BE=15–7=8(米)
A
D
C
B
E
答:梯子的底部滑开8米
∴CE=20
已知:AB=25,BE=7,
AC=4. 求BD的长度.
楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
现在你能完成这个任务吗
A
B
C
D
┌
联想的功能
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长, (2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
联想的功能
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
钢缆长几何
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CB上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
怎么做
我先将它数学化!
E
B
C
D
2m
400
5m
真知在实践中诞生
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.
求DE的长.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
单元知识网络
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
实际应用
画图,找直角三角形,利用三角函数
解直角三角形
A
C
B
