二次函数的图像与性质复习

(共13张PPT)
看到这些图形你想到了数学中什么知识？
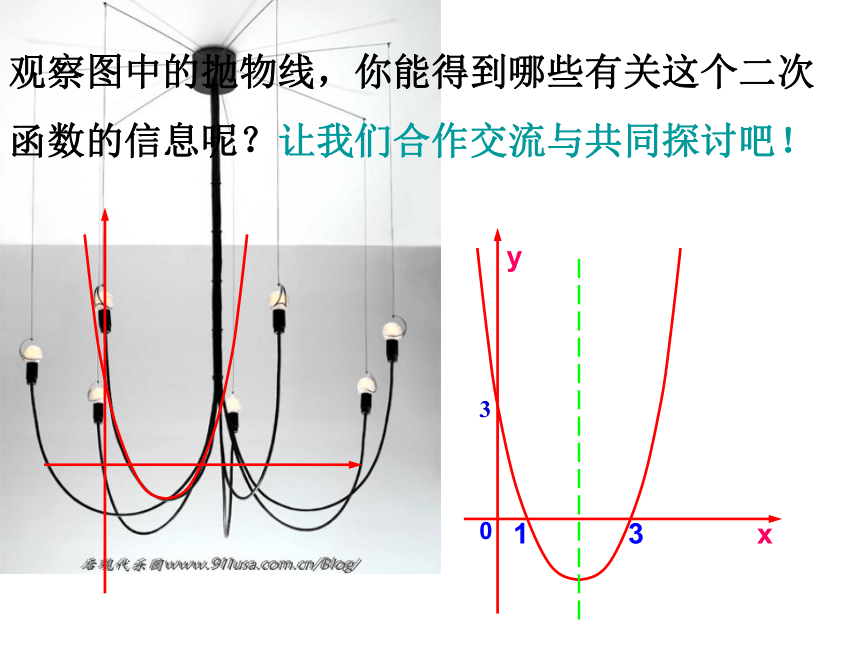
观察图中的抛物线，你能得到哪些有关这个二次
函数的信息呢？让我们合作交流与共同探讨吧！
1
3
3
0
x
y
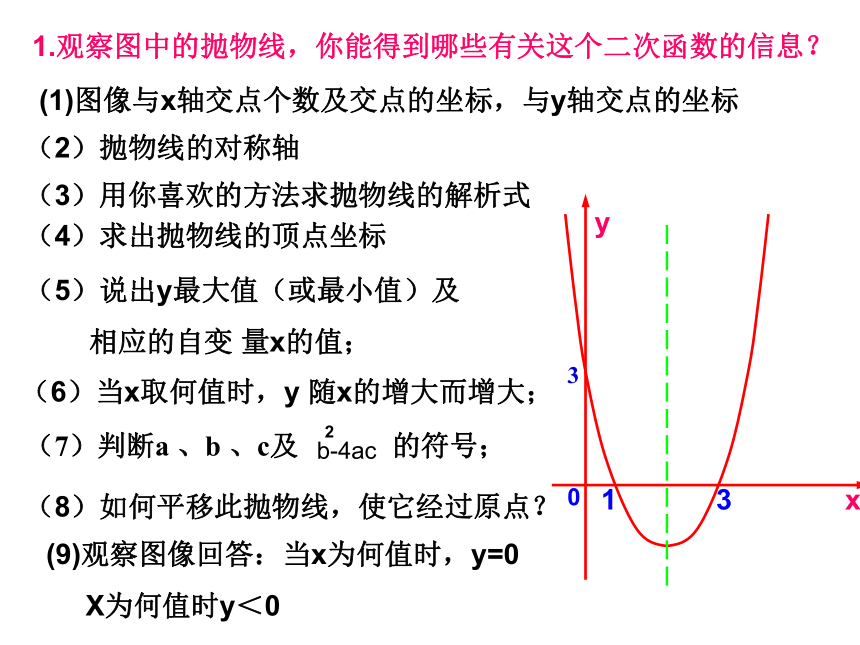
(1)图像与x轴交点个数及交点的坐标，与y轴交点的坐标
（2）抛物线的对称轴
（3）用你喜欢的方法求抛物线的解析式
（4）求出抛物线的顶点坐标
（5）说出y最大值（或最小值）及
相应的自变 量x的值；
（6）当x取何值时，y 随x的增大而增大；
b-4ac
2
（8）如何平移此抛物线，使它经过原点？
1.观察图中的抛物线，你能得到哪些有关这个二次函数的信息？
1
3
3
0
x
y
（7）判断a 、b 、c及 的符号；
(9)观察图像回答：当x为何值时，y=0
X为何值时y＜0
0
观察图中的抛物线，你能得到哪些有关这个二次函数的信息呢？
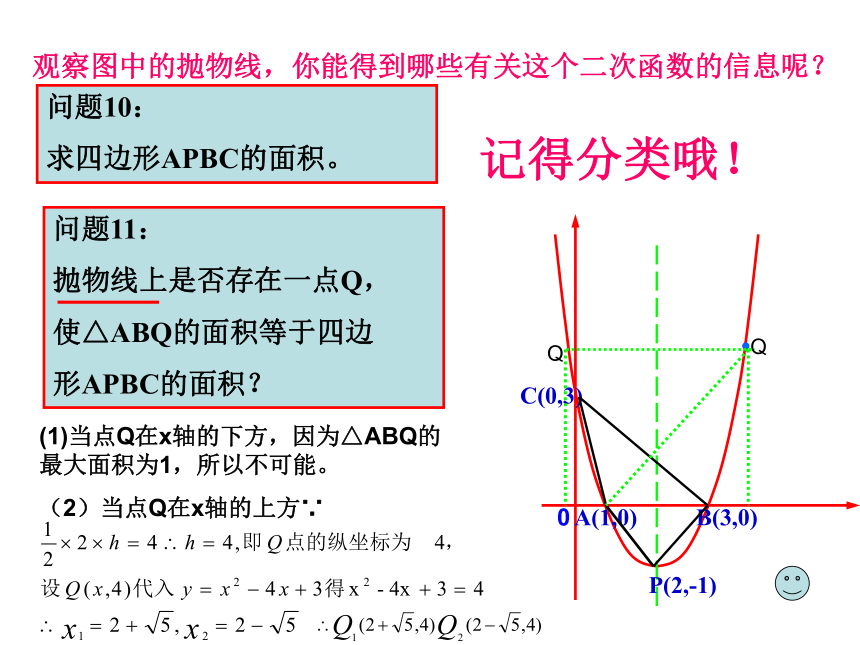
问题10：
求四边形APBC的面积。
问题11：
抛物线上是否存在一点Q，
使△ABQ的面积等于四边
形APBC的面积？
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
Q
●
Q
记得分类哦！
(1)当点Q在x轴的下方，因为△ABQ的最大面积为1，所以不可能。
（2）当点Q在x轴的上方∵
x
y
o
y = x2 - 4x + 3
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
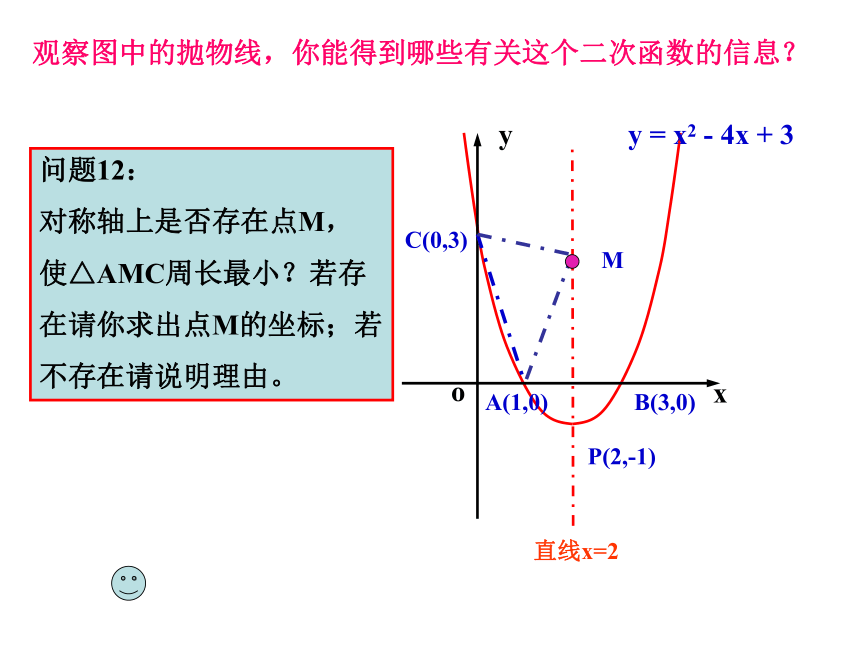
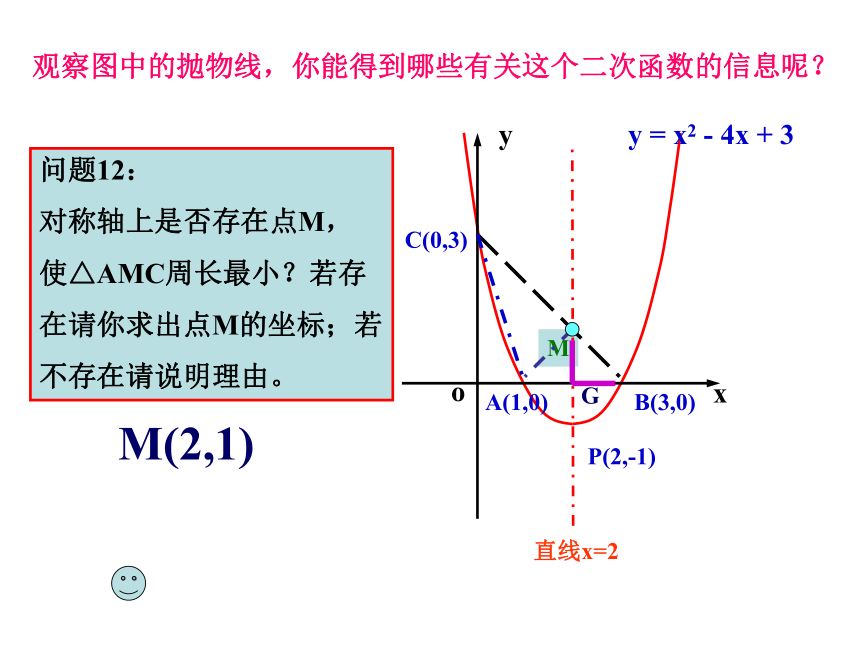
问题12：
对称轴上是否存在点M，
使△AMC周长最小？若存
在请你求出点M的坐标；若
不存在请说明理由。
M
观察图中的抛物线，你能得到哪些有关这个二次函数的信息？
M
x
y
o
y = x2 - 4x + 3
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
问题12：
对称轴上是否存在点M，
使△AMC周长最小？若存
在请你求出点M的坐标；若
不存在请说明理由。
G
M(2,1)
观察图中的抛物线，你能得到哪些有关这个二次函数的信息呢？
M
x
y
o
y = x2 - 4x + 3
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
问题13：
x轴上是否存在点N，
使△APN与△ABC相似？若存
在请你求出点N的坐标；若
不存在请说明理由。
G
观察图中的抛物线，你能得到哪些有关这个二次函数的信息呢？
N( ,0)
5
3
N(4,0)
1、对于函数y=-x2,下列结论中不正确的是( )
A.图象开口方向向下;
B.整个函数图象在x轴下方;
C.当x=0时,函数有最大值y=0;
D.图象关于y轴对称.
B
2、抛物线y=5(x-7)2-2的顶点坐标是( )
A.(-7,-2) B.(7,2)
C.(-7,2) D.(7,-2)
D
3、抛物线y=ax2+bx+c的图象如图,当x 时,
y随着x的增大而减小.
≤3
x
y
O
x=3
4、二次函数y=2x2-8x+c的最小值是0,那么c的值等于 .
8
5、若 （-0.5，y1）、（0.5，y2）、（2，y3）三点在函数 图象上，则y1 、y2 、y3三个值的大小
关系是 .
y1x
y
0
1
y = -x 2+2x+3
-1
3
4
7、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
(5)b2-4ac < 0
其中正确的结论的个数是（ ）
A 1个 B 2个 C 3个 D 4个
6.　根据下列表格的对应值：
x 3.23 3.24 3.25 3.26
ax2+bx+c －0.06 －0.02 0.03 0.09
判断方程(a≠0，a，b，c为常数)一个解x的范围是（ ）
A、3＜x＜3.23 　　　　　　 B、3.23＜x＜3.24
C、3.24＜x＜3.25 　　　　　 D、3.25 ＜x＜3.26
-1
1
0
y
x
C
C
这节课我们复习了哪些知识
你有什么收获
还有哪些疑惑
回顾与反思

名称 顶点式 一般式 交点式
二次函数解析式
对称轴
顶点坐标
增减性
a＞0
a＜0
最值 a＞0
a＜0
y=a(x+m)2+k
y=ax2+bx+c
y=a(x-x1)(x-x2)
直线x=-m
直线x=
直线x=
(-m,k)
( )
当x≤-m时，y随x的增大而减小;当x≥-m时,y随x的增大而增大
当x ≤ 时，y随x的增大而减小；当x ≥ 时y随x的增大而增大
当x≤-m时，y随的增大而增大；当x≥-m时,y随的增大而减小
当x≤ 时，y随x的增大而增大；当x≥ 时y随x的增大而减小
当 x=-m 时,y最小值=k
当x= 时,y最小值=
当x=-m时，y最大值=k
当x= 时,y最大值=
y
x
o
o
y
x