第三章 圆的基本性质复习(3.1-3.4)
文档属性
| 名称 | 第三章 圆的基本性质复习(3.1-3.4) |  | |
| 格式 | zip | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-20 22:04:32 | ||
图片预览





文档简介
(共21张PPT)
怎样将一个如图所示的破镜重圆?
C
B
D
圆的确定:不在同一直线上的三点确定一个圆。
∠B=90°
O
B
C
D
1.如图Rt△CBD中
(1)若两直角边为3cm和4cm则其外接 圆的半径为__cm
(2)若使点E在⊙O外则OE的长度
应满足什么条件?E在 ⊙O上呢?
E●
O
●
O
C
D
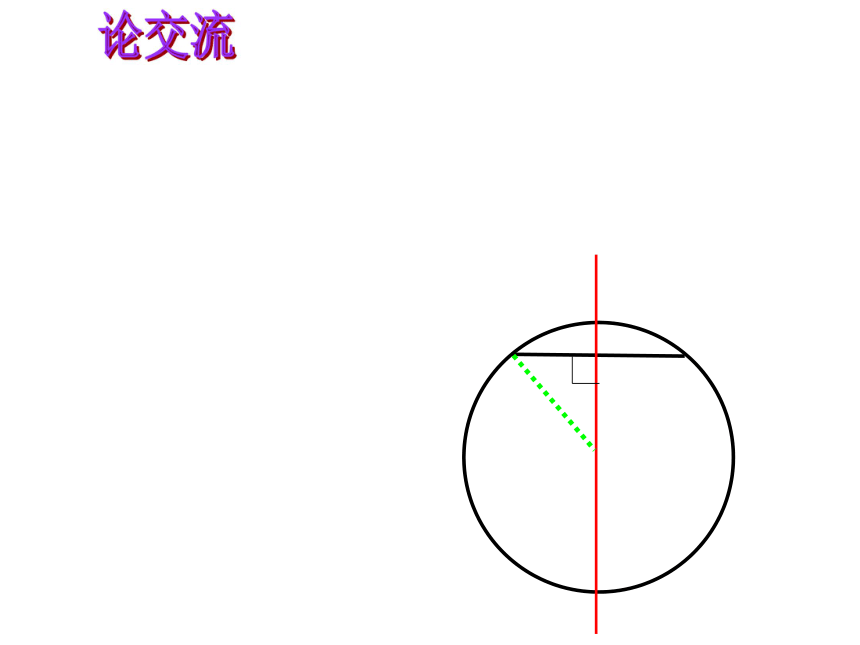
如图,CD是复原的破镜⊙O的弦,如何找到CD的对称轴呢 你有哪些方法
B
A
E
如图,已知⊙o的直径AB⊥弦CD于点E,
(1)若AB=10cm,CD=6cm, 求OE的长;
(2)若AE=1cm,CD=6cm, 求⊙o的半径;
弦长、半径、弦心距、弓高
只要具备其中两个量,
就可计算其余两个量.
●O
C
D
A
B
└
E
只要具备其中两个条件,
就可推出其余三个结论.
① AB是直径
③ CE=DE
② AB⊥CD
⌒
⌒
⑤ BC=BD
⌒
⌒
④ AC=AD
根据垂径定理与其逆定理可知,在下列五个条件中:
(弦CD不是直径)
●
O
C
D
C
D
C
D
C
D
E
F
图中有哪些相等的量
⌒
⌒
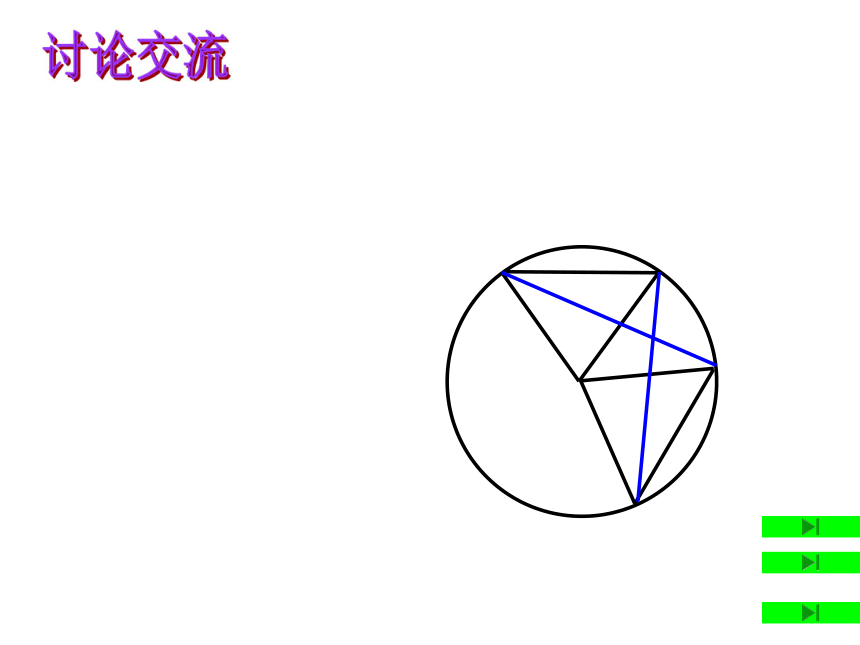
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF
求证:CE=FD
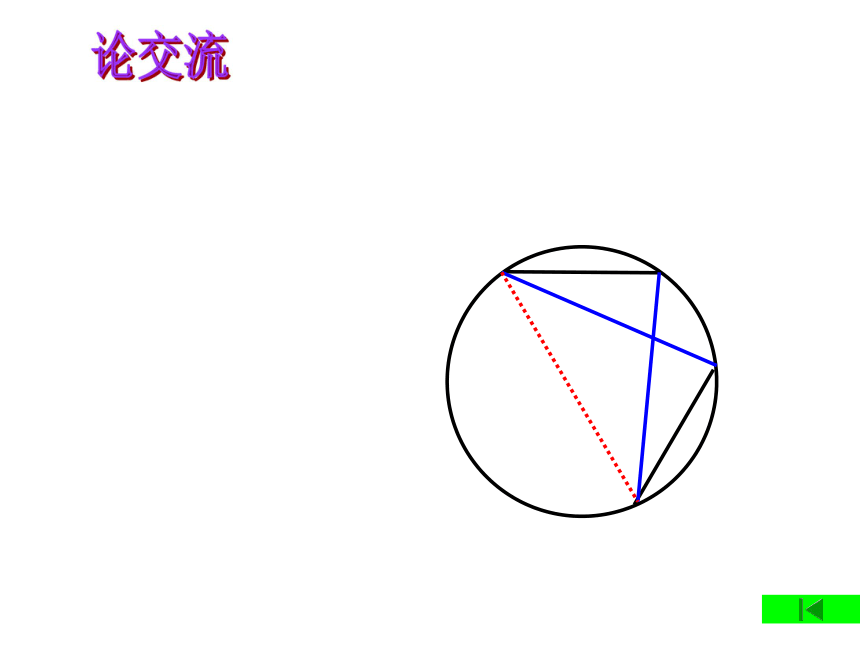
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF.
求证:CE=FD
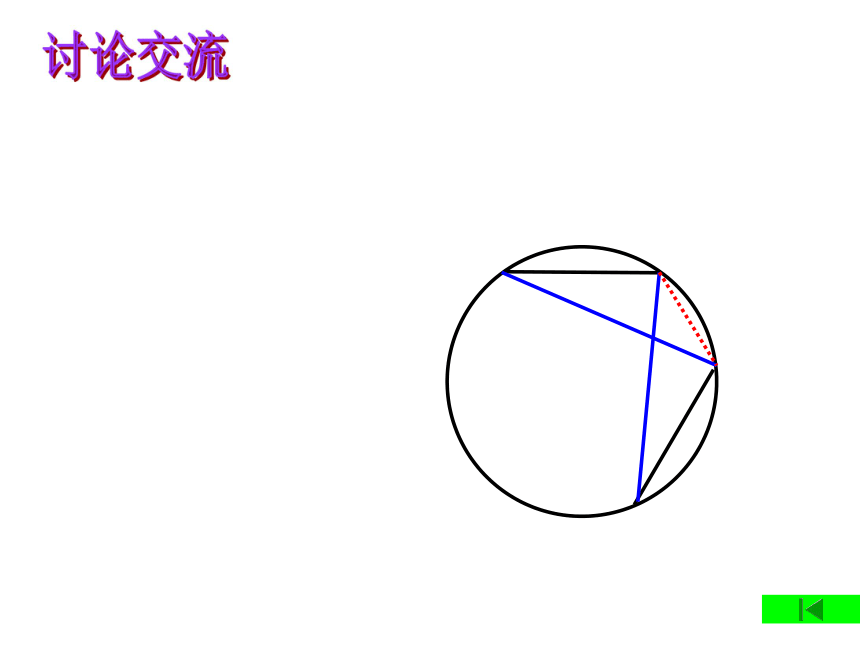
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF.
求证:CE=FD
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
所对的弧相等
所对弦相等
弦心距
相等圆心角
所对的圆周角相等
同圆或等圆中
只要其中一组量相等, 其余的量都对应相等.
●
O
如图,CD是复原的破镜⊙O的弦,将CD
向下平移到如图所示的位置。
C
D
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(1)求点B的坐标和⊙O的半径;
C
D
A
P
O
x
y
B
(2)当点P运动到什么位置时△CDP
的面积最大?求出此时P点的坐标和
△CDP的最大面积.
●P
y
C
D
A
O
x
B
E
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(2)当点P运动到什么位置时△CDP
的面积最大?求出此时P点的坐标和
△CDP的最大面积.
(1)求点B的坐标和⊙O的半径;
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(3)当点P运动到什么位置时四边形CADP为梯形?画出示意图并求 出此时∠PCD的度数
C
D
A
P
O
x
y
B
C
D
A
P
C
D
A
P
P●
y
C
D
A
O
x
B
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(4)当点P运动到BC中点时,连接BD,
BP并延长交 轴于E ,求CE的长。
x
E
1、已知 ⊙ O中,弦AB垂直于直径CD,垂足为P,
AB=6,CP=1,则 ⊙ O的半径为 -------------- 。
2、已知 ⊙ O的直径为10cm,A是⊙ O内一点,且OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。
A
B
C
D
O
P
O
A
5
8
3、在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.
50°或130°
图(1)
图(2)
4、如图:已知△ABC是圆O的内接三角形,
(1)点O是△ABC_____________的交点.
图中的弦有________________, 弦AB所对的弧有________.
(2)已知△ABC是等边三角形,则AB
的度数为_____,∠AOB=_____.
若圆O的半径为6,
这个三角形的边长为______.
O
A
C
B
⌒
D
三边中垂线
AB、BC、AC
⌒
⌒
AB、ACB
1200
1200
A
B
C
O
D
3.6
5、如图:△ABC内接于⊙O,弦AB=1.8,
∠ACB=30°,则⊙O的直径= 。
作圆的直径也是常用的辅助线
例1:C、D、E是⊙O上三个点,连接弧CD和弧CE的中点A、B的弦交弦CD、CE于F、G.求证:∠1=∠2.
C
D
O
E
A
B
F
G
1
2
3
4
7.已知:如图,EB为圆A直径,C、F为圆上点AF∥BC,
(1)求证:BF平分∠ABC
(2)若BF=8,BF:EF=2:1,
求圆A的半径。
(3)若C为BF中点,试判断
四边形ABCF的形状。
F
A
B
C
E
这节课我们复习了哪些知识
你有什么收获
还有哪些疑惑
圆
概念
圆心、半径、直径
弧、弦、弦心距
圆心角、圆周角
三角形外接圆、圆的内接三角形
圆的基本性质
点和圆的位置关系
不在同一直线上的
三点确定一个圆
轴对称性
垂径定理
及其逆定理
圆的中心对称性和旋转不变性
圆心角定理
圆周角定理
怎样将一个如图所示的破镜重圆?
C
B
D
圆的确定:不在同一直线上的三点确定一个圆。
∠B=90°
O
B
C
D
1.如图Rt△CBD中
(1)若两直角边为3cm和4cm则其外接 圆的半径为__cm
(2)若使点E在⊙O外则OE的长度
应满足什么条件?E在 ⊙O上呢?
E●
O
●
O
C
D
如图,CD是复原的破镜⊙O的弦,如何找到CD的对称轴呢 你有哪些方法
B
A
E
如图,已知⊙o的直径AB⊥弦CD于点E,
(1)若AB=10cm,CD=6cm, 求OE的长;
(2)若AE=1cm,CD=6cm, 求⊙o的半径;
弦长、半径、弦心距、弓高
只要具备其中两个量,
就可计算其余两个量.
●O
C
D
A
B
└
E
只要具备其中两个条件,
就可推出其余三个结论.
① AB是直径
③ CE=DE
② AB⊥CD
⌒
⌒
⑤ BC=BD
⌒
⌒
④ AC=AD
根据垂径定理与其逆定理可知,在下列五个条件中:
(弦CD不是直径)
●
O
C
D
C
D
C
D
C
D
E
F
图中有哪些相等的量
⌒
⌒
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF
求证:CE=FD
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF.
求证:CE=FD
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
●
O
C
D
E
F
图中有哪些相等的量
G
如图,在⊙O中,CD=EF.
求证:CE=FD
如图,CD是复原的破镜⊙O的弦,连接CO,DO,再把△COD绕o点顺时针旋转任意角度。
所对的弧相等
所对弦相等
弦心距
相等圆心角
所对的圆周角相等
同圆或等圆中
只要其中一组量相等, 其余的量都对应相等.
●
O
如图,CD是复原的破镜⊙O的弦,将CD
向下平移到如图所示的位置。
C
D
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(1)求点B的坐标和⊙O的半径;
C
D
A
P
O
x
y
B
(2)当点P运动到什么位置时△CDP
的面积最大?求出此时P点的坐标和
△CDP的最大面积.
●P
y
C
D
A
O
x
B
E
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(2)当点P运动到什么位置时△CDP
的面积最大?求出此时P点的坐标和
△CDP的最大面积.
(1)求点B的坐标和⊙O的半径;
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(3)当点P运动到什么位置时四边形CADP为梯形?画出示意图并求 出此时∠PCD的度数
C
D
A
P
O
x
y
B
C
D
A
P
C
D
A
P
P●
y
C
D
A
O
x
B
如图在⊙O中,弦CD=6,点A是CD的中点,∠CAD=120°,P是弦CD所对的优弧CBD上的一个动点(不运动到C,D)以点C为坐标原点,CD所在的直线为x轴,建立直角坐标系.
(4)当点P运动到BC中点时,连接BD,
BP并延长交 轴于E ,求CE的长。
x
E
1、已知 ⊙ O中,弦AB垂直于直径CD,垂足为P,
AB=6,CP=1,则 ⊙ O的半径为 -------------- 。
2、已知 ⊙ O的直径为10cm,A是⊙ O内一点,且OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。
A
B
C
D
O
P
O
A
5
8
3、在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.
50°或130°
图(1)
图(2)
4、如图:已知△ABC是圆O的内接三角形,
(1)点O是△ABC_____________的交点.
图中的弦有________________, 弦AB所对的弧有________.
(2)已知△ABC是等边三角形,则AB
的度数为_____,∠AOB=_____.
若圆O的半径为6,
这个三角形的边长为______.
O
A
C
B
⌒
D
三边中垂线
AB、BC、AC
⌒
⌒
AB、ACB
1200
1200
A
B
C
O
D
3.6
5、如图:△ABC内接于⊙O,弦AB=1.8,
∠ACB=30°,则⊙O的直径= 。
作圆的直径也是常用的辅助线
例1:C、D、E是⊙O上三个点,连接弧CD和弧CE的中点A、B的弦交弦CD、CE于F、G.求证:∠1=∠2.
C
D
O
E
A
B
F
G
1
2
3
4
7.已知:如图,EB为圆A直径,C、F为圆上点AF∥BC,
(1)求证:BF平分∠ABC
(2)若BF=8,BF:EF=2:1,
求圆A的半径。
(3)若C为BF中点,试判断
四边形ABCF的形状。
F
A
B
C
E
这节课我们复习了哪些知识
你有什么收获
还有哪些疑惑
圆
概念
圆心、半径、直径
弧、弦、弦心距
圆心角、圆周角
三角形外接圆、圆的内接三角形
圆的基本性质
点和圆的位置关系
不在同一直线上的
三点确定一个圆
轴对称性
垂径定理
及其逆定理
圆的中心对称性和旋转不变性
圆心角定理
圆周角定理
同课章节目录
