2021-2022学年浙教版 九年级数学上册第四章相似三角形培优测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版 九年级数学上册第四章相似三角形培优测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 12:01:48 | ||
图片预览


文档简介
浙教版2021-2022学年九年级数学上册第四章相似三角形培优测试卷
一、单选题(共10题;共30分)
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则 的值为( )
A. B. C. D.
2.如图,已知l3∥l4∥l5 , 它们依次交直线l1、l2于点E,A,C和点D,A,B,如果AD=2,AE=3,AB=4,那么CE=( )
A. 6 B. C. 9 D.
3.已知 ,那么下列等式一定成立的是( )
A. x=2,y=3 B. C. D.
4.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角 ,窗户的高在教室地面上的影长 米,窗户的下檐到教室地面的距离 米(点 、 、 在同一直线上),则窗户的高 为( )
A. 米 B. 3米 C. 2米 D. 1.5米
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A. 3:4 B. 9:16 C. 9:1 D. 3:1
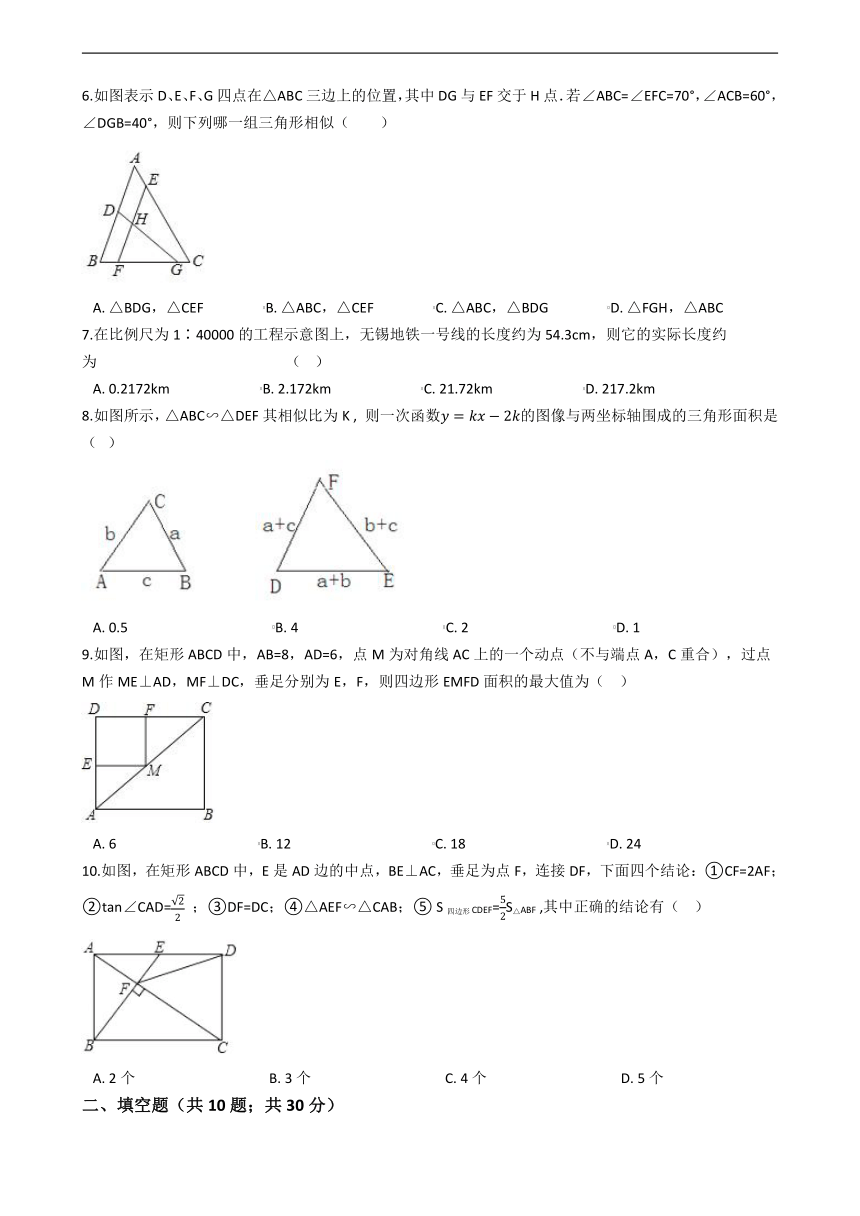
6.如图表示D、E、F、G四点在△ABC三边上的位置,其中DG与EF交于H点.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列哪一组三角形相似( )
A. △BDG,△CEF B. △ABC,△CEF C. △ABC,△BDG D. △FGH,△ABC
7.在比例尺为1∶40000的工程示意图上,无锡地铁一号线的长度约为54.3cm,则它的实际长度约为 ( )
A. 0.2172km B. 2.172km C. 21.72km D. 217.2km
8.如图所示,△ABC∽△DEF 其相似比为K , 则一次函数的图像与两坐标轴围成的三角形面积是( )
A. 0.5 B. 4 C. 2 D. 1
9.如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
A. 6 B. 12 C. 18 D. 24
10.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD= ;③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF=S△ABF ,其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(共10题;共30分)
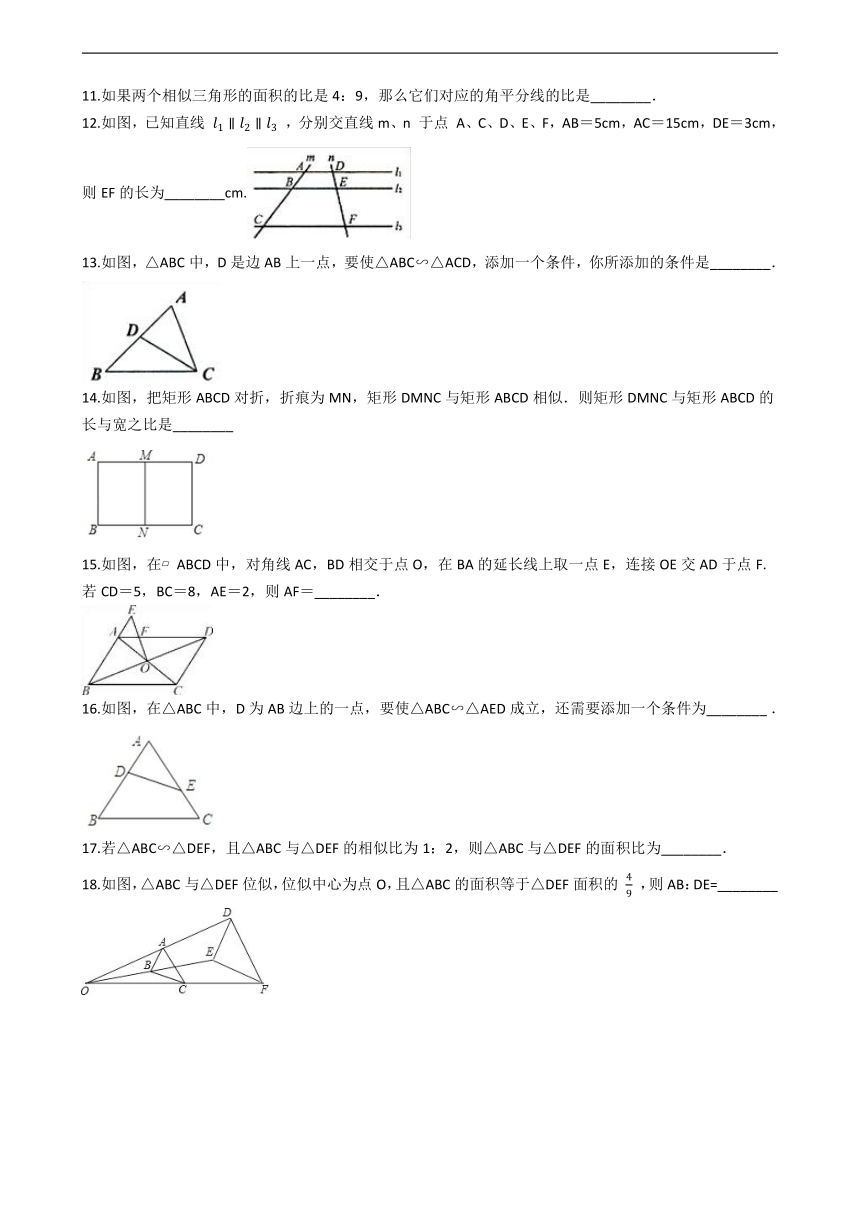
11.如果两个相似三角形的面积的比是4:9,那么它们对应的角平分线的比是________.
12.如图,已知直线 ,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为________cm.
13.如图,△ABC中,D是边AB上一点,要使△ABC∽△ACD,添加一个条件,你所添加的条件是________.
14.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似.则矩形DMNC与矩形ABCD的长与宽之比是________
15.如图,在 ABCD中,对角线AC,BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=________.
16.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为________ .
17.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比为________.
18.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AB:DE=________
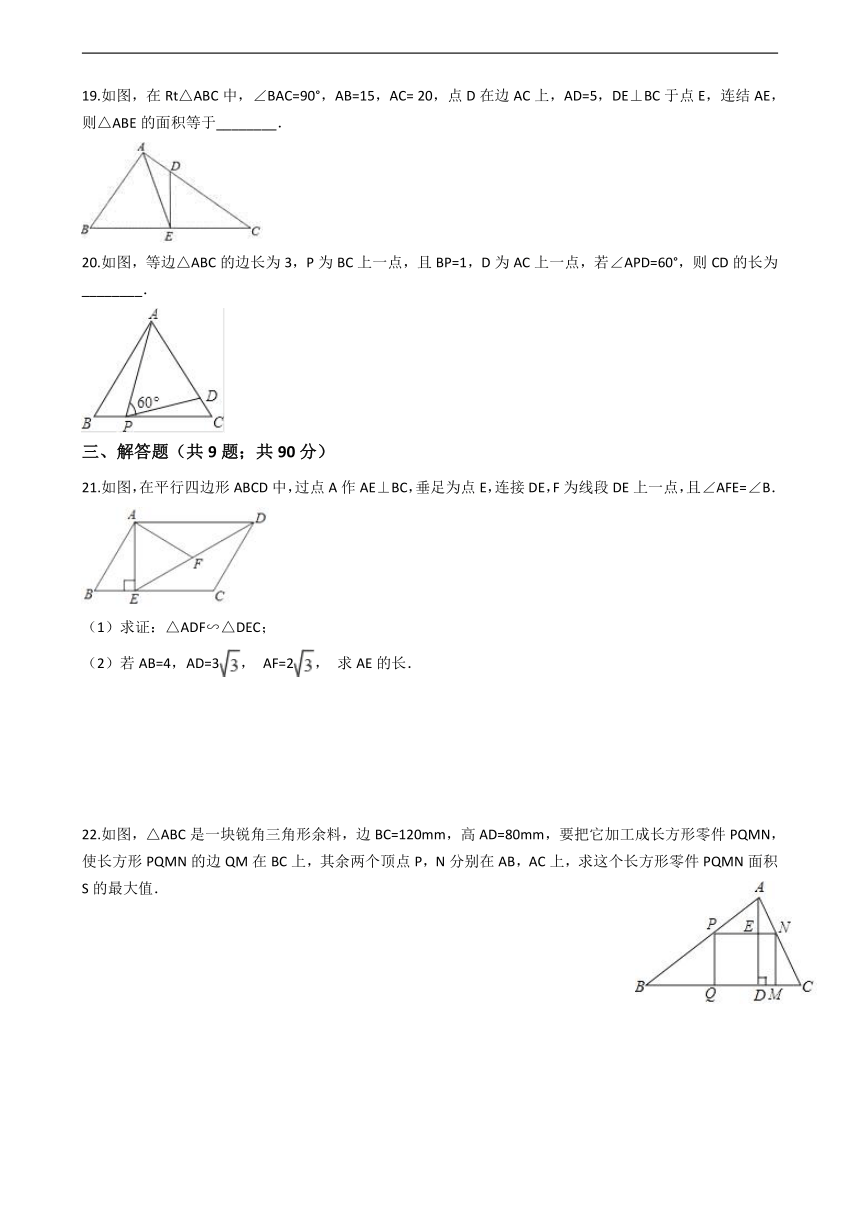
19.如图,在Rt△ABC中,∠BAC=90°,AB=15,AC= 20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于________.
20.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为________.
三、解答题(共9题;共90分)
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3, AF=2, 求AE的长.
22.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.
23.如图,在△ABC中,∠B 90°,AB 4,BC 2,以AC为边作△ACE,∠ACE 90°,AC=CE,延长BC至点D,使CD 5,连接DE.求证:△ABC∽△CED.
24.如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
25.如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 = .
(1)求证:AB∥CD;
(2)如果AD2=DG DE,求证: = .
26.在平面直角坐标系xOy中,反比例函数 的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
27.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
28.如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
29.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE·CA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD= ,求⊙O的半径.
答案
一、单选题
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】2:3
【考点】相似三角形的性质
【解析】【解答】先根据相似三角形面积的比是4:9,求出其相似比是2:3,再根据其对应的角平分线的比等于相似比,可知它们对应的角平分线比是2:3.
故答案为:2:3.
【分析】因为相似三角形面积的比等于相似比的平方,所以可得其相似比是2:3,而其对应的角平分线的比等于相似比,所以它们对应的角平分线比是2:3.
12.【答案】6
【考点】平行线分线段成比例
【解析】【解答】∵ ,∴ ,即 ,解得,EF=6.【分析】根据平行线分线段成比例,结合题中所给的数据建立比例关系,即可得到EF的长度。
13.【答案】∠ACD=∠B
【考点】相似三角形的判定
【解析】【解答】解:∵∠BAC=∠CAD,
∴当∠ACD=∠B或∠ADC=∠ACB或 时,△ACD∽△ABC.
故答案为:∠ACD=∠B或∠ADC=∠ACB或 .
【分析】观察图形。图形中隐含公共角∠A,要证明△ABC∽△ACD,利用相似三角形的判定定理:有两组对应角相等的两三角形相似,因此可添加另外的两组对应角相等;两组对应边成比例且夹角相等的两三角形相似,可添加AD、AC、AC、AB对应成比例,就可解决问题。
14.【答案】
【考点】相似多边形的性质
【解析】【解答】解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴
即y2=x2 .
∴x:y=:1.
故答案为::1.
【分析】设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
15.【答案】
【考点】三角形中位线定理,平行四边形的性质,相似三角形的判定与性质
【解析】【解答】解:过O点作OM∥AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OM是△ABD的中位线,
∴AM=BM= AB= ,OM= BC=4.
∵AF∥OM,
∴△AEF∽△MEO,∴ ,
∴ ,
∴AF= .
故答案为: .
【分析】过O点作OM∥AD,根据平行四边形的性质,可证得OM是△ABD的中位线,就可求出AM、OM的长,再根据平行得三角形相似,去证明△AEF∽△MEO,利用相似三角形的性质,可证得对应边成比例,从而可求出AF的长。
16.【答案】 ∠ADE=∠C 或∠AED=∠B或
【考点】相似三角形的判定
【解析】【解答】解:∵∠ABC=∠AED,∠A=∠A,
∴△ABC∽△AED,
故添加条件∠ABC=∠AED即可求得△ABC∽△AED.
同理可得:∠ADE=∠C 或∠AED=∠B或可以得出△ABC∽△AED;
故答案为:∠ADE=∠C 或∠AED=∠B或 .
【分析】根据相似三角形对应角相等,可得∠ABC=∠AED,故添加条件∠ABC=∠AED即可求得△ABC∽△AED,即可解题.
17.【答案】1:4
【考点】相似三角形的性质
【解析】【解答】解:∵△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故答案为:1:4.
【分析】相似三角形的面积比等于相似比的平方。
18.【答案】2:3
【考点】位似变换
【解析】【解答】解:∵△ABC与△DEF位似,位似中心为点O,
∴△ABC∽△DEF,
∴△ABC的面积:△DEF面积=( )2= ,
∴AB:DE=2:3,
故答案为:2:3.
【分析】由△ABC经过位似变换得到△DEF,点O是位似中心,根据位似图形的性质,即可得AB∥DE,即可求得△ABC的面积:△DEF面积= ,得到AB:DE═2:3.
19.【答案】78
【考点】勾股定理,相似三角形的判定与性质
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,AB=15,AC= 20,
∴
BC=25
∴△ABC的面积=ABAC=×15×20=150
∵CD=AC-AD=20-5-15
∵DE⊥BC,
∴∠DEC=∠BAC=90°
∠C=∠C
∴△CDE∽△CBA
即CE:20=15:25
解之:CE=12
∴BE=BC-CE=13
∵S△ABE:S△ABC=BE:BC=13:25
∴S△ABE:150=13:25
解之:S△ABE=78
故答案为:78
【分析】根据题意,利用勾股定理求出BC的长,就可求出△ABC的面积,再证明△CDE∽△CBA,利用相似三角形的性质,得出对应边成比例,求出CE的长,从而求出BE的长,然后根据S△ABE:S△ABC=BE:BC,建立方程,求出△ABE的面积即可。
20.【答案】
【考点】相似三角形的判定与性质
【解析】【解答】:∵△ABC是等边三角形,
∴AB=BC=AC=3,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC ,
即∠B=∠C , ∠BAP=∠DPC ,
∴△BAP∽△CPD ,
∴ = ,
∵AB=BC=3,CP=BC-BP=3-1=2,BP=1,
即 = ,
解得:CD= ,
故答案为: .
【分析】根据等边三角形性质求出AB=BC=AC=3,∠B=∠C=60°,推出∠BAP=∠DPC , 证△BAP∽△CPD , 得出 = ,代入求出即可.
三、解答题
21.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴,
∴DE=.
在Rt△ADE中,由勾股定理得:AE=.
22.解:设长方形零件PQMN的边PN=a,PQ=x,则AE=80﹣x. ∵PN∥BC,
∴△APN∽△ABC.
∴ = .
因此, = .
解得a=120﹣ x.
所以长方形PQMN的面积S=xa=x(120﹣ x)=﹣ x2+120x.
当x=﹣ =40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2
23.解:∵ ∠B=90°,AB=4,BC=2,
∴ .
∵ CE=AC,
∴ .
∵ CD=5,
∴ .
∵ ∠B=90°,∠ACE=90°,
∴ ∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴ ∠BAC=∠DCE.
∴ △ABC∽△CED.
24.解:(1)设直线AB的解析式为y=kx+b,
由题意,得
解得:
所以,直线AB的解析式为y=-x+12;
(2)由AO=12,BO=16得AB=20,
所以AP=t,AQ=20-2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以,
解得t=(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以,
解得t=(秒);
∴当t为秒或秒时,△APQ与△AOB相似;
(3)过Q点作QE⊥Y轴于点E,
由△AQE∽△AOB知:
即:
解得:QE=
又S△APQ=
解得:t1=2,t2=8
(4)∵QE=16-t
∴S△APQ=AP QE=t(16-t)=-t2+8t=-(t-5)2+20
∴当t=5时,△APQ的面积最大,最大面积是20个平方单位.
25.(1)证明:∵AD∥BC, ∴△ADG∽△CEG,
∴ ,
∵ = ,
∴ ,
∴AB∥CD
(2)证明:∵AD∥BC, ∴△ADG∽△CEG,
∴ ,
∴ = ,
∴ = ,
∵AD2=DG DE,
∴ = ,
∵AD∥BC,
∴ = ,
∴ = .
26.(1)解:∵反比例函数 的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y=
(2)解:作AC⊥x轴于C,BD⊥x轴于D,
∵AC∥BD,
∴△APC∽△BPD,
∴ ,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为﹣3,
代入y= 得,﹣3= ,解得x=﹣2,
∴B(﹣2,﹣3),
设直线AB的解析式为y=kx+b,
∴ ,解得 ,
∴直线AB的解析式为y=3x+3,
令y=0,则求得x=﹣1,
∴P(﹣1,0).
27(1)证明:连结AE,如图,∵AC为⊙O的直径,∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE;
(2)解:连结DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,而∠DBE=∠CBA,
∴△BED∽△BAC,
∴ ,即 ,
∴BA=9,
∴AC=BA=9.
28.(1)解:在矩形OABC中,
∵B(4,6),
∴BC边中点D的坐标为(2,6),
∵又曲线y= 的图象经过点(2,6),
∴k=12,
∵E点在AB上,
∴E点的横坐标为4,
∵y= 经过点E,
∴E点纵坐标为3,
∴E点坐标为(4,3)
(2)解:由(1)得,BD=2,BE=3,BC=4,
∵△FBC∽△DEB,
∴ = ,即 = ,
∴CF= ,
∴OF= ,即点F的坐标为(0, ),
设直线FB的解析式为y=kx+b,而直线FB经过B(4,6),F(0, ),
∴ ,解得 ,
∴直线BF的解析式为y= x+
29(1)证明:∵DC2=CE·CA,
∴,
∵∠DCE=∠ACD,
∴△CDE~△CAD,
∴∠CDE=∠CAD,
又∵∠CBD=∠CAD,
∴∠CDE=∠CBD,
∴CD=CB.
(2)解:连结OC(如图),设⊙O的半径为r,
由(1)知CD=CB,
∴弧CD=弧CB,
∴∠CDB=∠CBD=∠CAB=∠CAD=∠BAD,∠BOC=2∠CAB,
∴∠BOC=∠BAD,
∴OC∥AD,
∴,
∵PB=OB,
∴PB=OB=OA=r,PO=2r,
∴=2,
∵CD=2,
∴PC=4,PD=PC+CD=6,
又∵∠PCB=∠CDB+∠CBD,∠PAD=∠PACB+∠CAD,
∴∠PCB=∠PAD,
∵∠CPB=∠APD,
∴△PCB~△PAD,
∴,
即,
解得:r=4.
即⊙O的半径为4.
一、单选题(共10题;共30分)
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则 的值为( )
A. B. C. D.
2.如图,已知l3∥l4∥l5 , 它们依次交直线l1、l2于点E,A,C和点D,A,B,如果AD=2,AE=3,AB=4,那么CE=( )
A. 6 B. C. 9 D.
3.已知 ,那么下列等式一定成立的是( )
A. x=2,y=3 B. C. D.
4.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角 ,窗户的高在教室地面上的影长 米,窗户的下檐到教室地面的距离 米(点 、 、 在同一直线上),则窗户的高 为( )
A. 米 B. 3米 C. 2米 D. 1.5米
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A. 3:4 B. 9:16 C. 9:1 D. 3:1
6.如图表示D、E、F、G四点在△ABC三边上的位置,其中DG与EF交于H点.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列哪一组三角形相似( )
A. △BDG,△CEF B. △ABC,△CEF C. △ABC,△BDG D. △FGH,△ABC
7.在比例尺为1∶40000的工程示意图上,无锡地铁一号线的长度约为54.3cm,则它的实际长度约为 ( )
A. 0.2172km B. 2.172km C. 21.72km D. 217.2km
8.如图所示,△ABC∽△DEF 其相似比为K , 则一次函数的图像与两坐标轴围成的三角形面积是( )
A. 0.5 B. 4 C. 2 D. 1
9.如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
A. 6 B. 12 C. 18 D. 24
10.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD= ;③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF=S△ABF ,其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(共10题;共30分)
11.如果两个相似三角形的面积的比是4:9,那么它们对应的角平分线的比是________.
12.如图,已知直线 ,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为________cm.
13.如图,△ABC中,D是边AB上一点,要使△ABC∽△ACD,添加一个条件,你所添加的条件是________.
14.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似.则矩形DMNC与矩形ABCD的长与宽之比是________
15.如图,在 ABCD中,对角线AC,BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=________.
16.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为________ .
17.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比为________.
18.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AB:DE=________
19.如图,在Rt△ABC中,∠BAC=90°,AB=15,AC= 20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于________.
20.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为________.
三、解答题(共9题;共90分)
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3, AF=2, 求AE的长.
22.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.
23.如图,在△ABC中,∠B 90°,AB 4,BC 2,以AC为边作△ACE,∠ACE 90°,AC=CE,延长BC至点D,使CD 5,连接DE.求证:△ABC∽△CED.
24.如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
25.如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 = .
(1)求证:AB∥CD;
(2)如果AD2=DG DE,求证: = .
26.在平面直角坐标系xOy中,反比例函数 的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
27.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
28.如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
29.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE·CA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD= ,求⊙O的半径.
答案
一、单选题
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】2:3
【考点】相似三角形的性质
【解析】【解答】先根据相似三角形面积的比是4:9,求出其相似比是2:3,再根据其对应的角平分线的比等于相似比,可知它们对应的角平分线比是2:3.
故答案为:2:3.
【分析】因为相似三角形面积的比等于相似比的平方,所以可得其相似比是2:3,而其对应的角平分线的比等于相似比,所以它们对应的角平分线比是2:3.
12.【答案】6
【考点】平行线分线段成比例
【解析】【解答】∵ ,∴ ,即 ,解得,EF=6.【分析】根据平行线分线段成比例,结合题中所给的数据建立比例关系,即可得到EF的长度。
13.【答案】∠ACD=∠B
【考点】相似三角形的判定
【解析】【解答】解:∵∠BAC=∠CAD,
∴当∠ACD=∠B或∠ADC=∠ACB或 时,△ACD∽△ABC.
故答案为:∠ACD=∠B或∠ADC=∠ACB或 .
【分析】观察图形。图形中隐含公共角∠A,要证明△ABC∽△ACD,利用相似三角形的判定定理:有两组对应角相等的两三角形相似,因此可添加另外的两组对应角相等;两组对应边成比例且夹角相等的两三角形相似,可添加AD、AC、AC、AB对应成比例,就可解决问题。
14.【答案】
【考点】相似多边形的性质
【解析】【解答】解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴
即y2=x2 .
∴x:y=:1.
故答案为::1.
【分析】设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
15.【答案】
【考点】三角形中位线定理,平行四边形的性质,相似三角形的判定与性质
【解析】【解答】解:过O点作OM∥AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OM是△ABD的中位线,
∴AM=BM= AB= ,OM= BC=4.
∵AF∥OM,
∴△AEF∽△MEO,∴ ,
∴ ,
∴AF= .
故答案为: .
【分析】过O点作OM∥AD,根据平行四边形的性质,可证得OM是△ABD的中位线,就可求出AM、OM的长,再根据平行得三角形相似,去证明△AEF∽△MEO,利用相似三角形的性质,可证得对应边成比例,从而可求出AF的长。
16.【答案】 ∠ADE=∠C 或∠AED=∠B或
【考点】相似三角形的判定
【解析】【解答】解:∵∠ABC=∠AED,∠A=∠A,
∴△ABC∽△AED,
故添加条件∠ABC=∠AED即可求得△ABC∽△AED.
同理可得:∠ADE=∠C 或∠AED=∠B或可以得出△ABC∽△AED;
故答案为:∠ADE=∠C 或∠AED=∠B或 .
【分析】根据相似三角形对应角相等,可得∠ABC=∠AED,故添加条件∠ABC=∠AED即可求得△ABC∽△AED,即可解题.
17.【答案】1:4
【考点】相似三角形的性质
【解析】【解答】解:∵△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故答案为:1:4.
【分析】相似三角形的面积比等于相似比的平方。
18.【答案】2:3
【考点】位似变换
【解析】【解答】解:∵△ABC与△DEF位似,位似中心为点O,
∴△ABC∽△DEF,
∴△ABC的面积:△DEF面积=( )2= ,
∴AB:DE=2:3,
故答案为:2:3.
【分析】由△ABC经过位似变换得到△DEF,点O是位似中心,根据位似图形的性质,即可得AB∥DE,即可求得△ABC的面积:△DEF面积= ,得到AB:DE═2:3.
19.【答案】78
【考点】勾股定理,相似三角形的判定与性质
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,AB=15,AC= 20,
∴
BC=25
∴△ABC的面积=ABAC=×15×20=150
∵CD=AC-AD=20-5-15
∵DE⊥BC,
∴∠DEC=∠BAC=90°
∠C=∠C
∴△CDE∽△CBA
即CE:20=15:25
解之:CE=12
∴BE=BC-CE=13
∵S△ABE:S△ABC=BE:BC=13:25
∴S△ABE:150=13:25
解之:S△ABE=78
故答案为:78
【分析】根据题意,利用勾股定理求出BC的长,就可求出△ABC的面积,再证明△CDE∽△CBA,利用相似三角形的性质,得出对应边成比例,求出CE的长,从而求出BE的长,然后根据S△ABE:S△ABC=BE:BC,建立方程,求出△ABE的面积即可。
20.【答案】
【考点】相似三角形的判定与性质
【解析】【解答】:∵△ABC是等边三角形,
∴AB=BC=AC=3,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC ,
即∠B=∠C , ∠BAP=∠DPC ,
∴△BAP∽△CPD ,
∴ = ,
∵AB=BC=3,CP=BC-BP=3-1=2,BP=1,
即 = ,
解得:CD= ,
故答案为: .
【分析】根据等边三角形性质求出AB=BC=AC=3,∠B=∠C=60°,推出∠BAP=∠DPC , 证△BAP∽△CPD , 得出 = ,代入求出即可.
三、解答题
21.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴,
∴DE=.
在Rt△ADE中,由勾股定理得:AE=.
22.解:设长方形零件PQMN的边PN=a,PQ=x,则AE=80﹣x. ∵PN∥BC,
∴△APN∽△ABC.
∴ = .
因此, = .
解得a=120﹣ x.
所以长方形PQMN的面积S=xa=x(120﹣ x)=﹣ x2+120x.
当x=﹣ =40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2
23.解:∵ ∠B=90°,AB=4,BC=2,
∴ .
∵ CE=AC,
∴ .
∵ CD=5,
∴ .
∵ ∠B=90°,∠ACE=90°,
∴ ∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴ ∠BAC=∠DCE.
∴ △ABC∽△CED.
24.解:(1)设直线AB的解析式为y=kx+b,
由题意,得
解得:
所以,直线AB的解析式为y=-x+12;
(2)由AO=12,BO=16得AB=20,
所以AP=t,AQ=20-2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以,
解得t=(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以,
解得t=(秒);
∴当t为秒或秒时,△APQ与△AOB相似;
(3)过Q点作QE⊥Y轴于点E,
由△AQE∽△AOB知:
即:
解得:QE=
又S△APQ=
解得:t1=2,t2=8
(4)∵QE=16-t
∴S△APQ=AP QE=t(16-t)=-t2+8t=-(t-5)2+20
∴当t=5时,△APQ的面积最大,最大面积是20个平方单位.
25.(1)证明:∵AD∥BC, ∴△ADG∽△CEG,
∴ ,
∵ = ,
∴ ,
∴AB∥CD
(2)证明:∵AD∥BC, ∴△ADG∽△CEG,
∴ ,
∴ = ,
∴ = ,
∵AD2=DG DE,
∴ = ,
∵AD∥BC,
∴ = ,
∴ = .
26.(1)解:∵反比例函数 的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y=
(2)解:作AC⊥x轴于C,BD⊥x轴于D,
∵AC∥BD,
∴△APC∽△BPD,
∴ ,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为﹣3,
代入y= 得,﹣3= ,解得x=﹣2,
∴B(﹣2,﹣3),
设直线AB的解析式为y=kx+b,
∴ ,解得 ,
∴直线AB的解析式为y=3x+3,
令y=0,则求得x=﹣1,
∴P(﹣1,0).
27(1)证明:连结AE,如图,∵AC为⊙O的直径,∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE;
(2)解:连结DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,而∠DBE=∠CBA,
∴△BED∽△BAC,
∴ ,即 ,
∴BA=9,
∴AC=BA=9.
28.(1)解:在矩形OABC中,
∵B(4,6),
∴BC边中点D的坐标为(2,6),
∵又曲线y= 的图象经过点(2,6),
∴k=12,
∵E点在AB上,
∴E点的横坐标为4,
∵y= 经过点E,
∴E点纵坐标为3,
∴E点坐标为(4,3)
(2)解:由(1)得,BD=2,BE=3,BC=4,
∵△FBC∽△DEB,
∴ = ,即 = ,
∴CF= ,
∴OF= ,即点F的坐标为(0, ),
设直线FB的解析式为y=kx+b,而直线FB经过B(4,6),F(0, ),
∴ ,解得 ,
∴直线BF的解析式为y= x+
29(1)证明:∵DC2=CE·CA,
∴,
∵∠DCE=∠ACD,
∴△CDE~△CAD,
∴∠CDE=∠CAD,
又∵∠CBD=∠CAD,
∴∠CDE=∠CBD,
∴CD=CB.
(2)解:连结OC(如图),设⊙O的半径为r,
由(1)知CD=CB,
∴弧CD=弧CB,
∴∠CDB=∠CBD=∠CAB=∠CAD=∠BAD,∠BOC=2∠CAB,
∴∠BOC=∠BAD,
∴OC∥AD,
∴,
∵PB=OB,
∴PB=OB=OA=r,PO=2r,
∴=2,
∵CD=2,
∴PC=4,PD=PC+CD=6,
又∵∠PCB=∠CDB+∠CBD,∠PAD=∠PACB+∠CAD,
∴∠PCB=∠PAD,
∵∠CPB=∠APD,
∴△PCB~△PAD,
∴,
即,
解得:r=4.
即⊙O的半径为4.
同课章节目录
