第七章 一次函数复习

(共34张PPT)
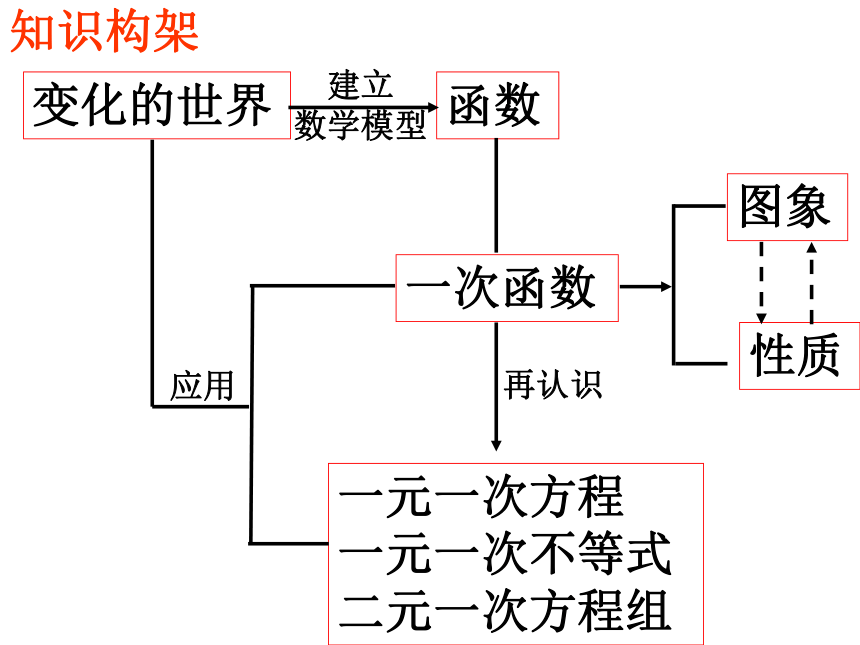
知识构架
变化的世界
函数
一次函数
一元一次方程
一元一次不等式
二元一次方程组
图象
性质
建立
数学模型
应用
再认识
一、知识要点：
　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。
kx ＋b
≠０
= ０
≠０
kx
★理解一次函数概念应注意下面两点：
　　⑴、解析式中自变量x的次数是___次，⑵、比例系数_____。
1
K≠0
　　2、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。
　　 3、一次函数y=kx+b(k≠0)的图象是过点（0，_
__),（____，0)的__________。
0，0
1，k
一条直线
b
一条直线
4、正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而____。
　　⑵当k<0时，图象过______象限；y随x的增大而____。
一、三
增大
二、四
减小
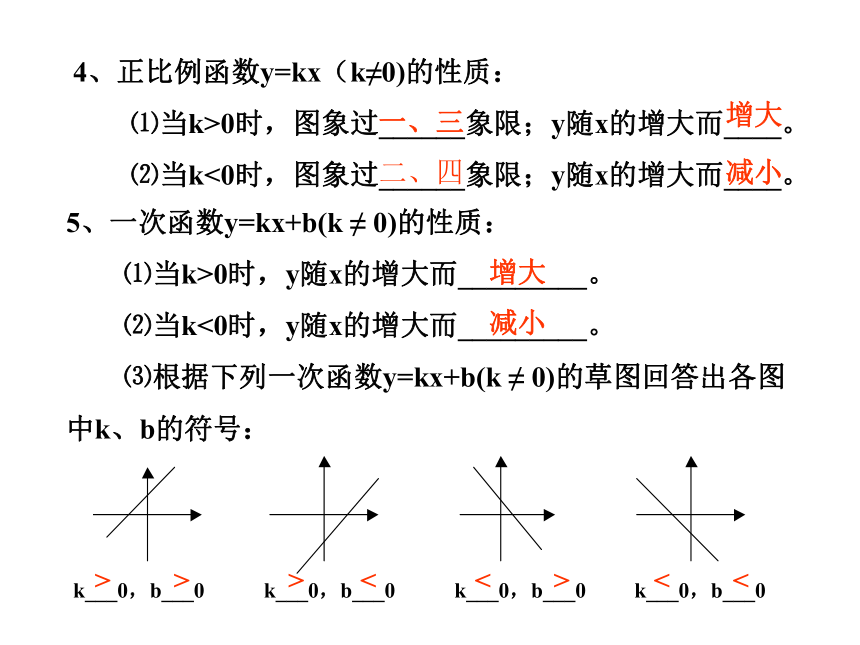
5、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号：
增大
减小
k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0
<
<
>
<
<
>
>
>
(1). 待定系数法; (2).实际问题的应用
(3). 解决方程,不等式,方程组的有关问题
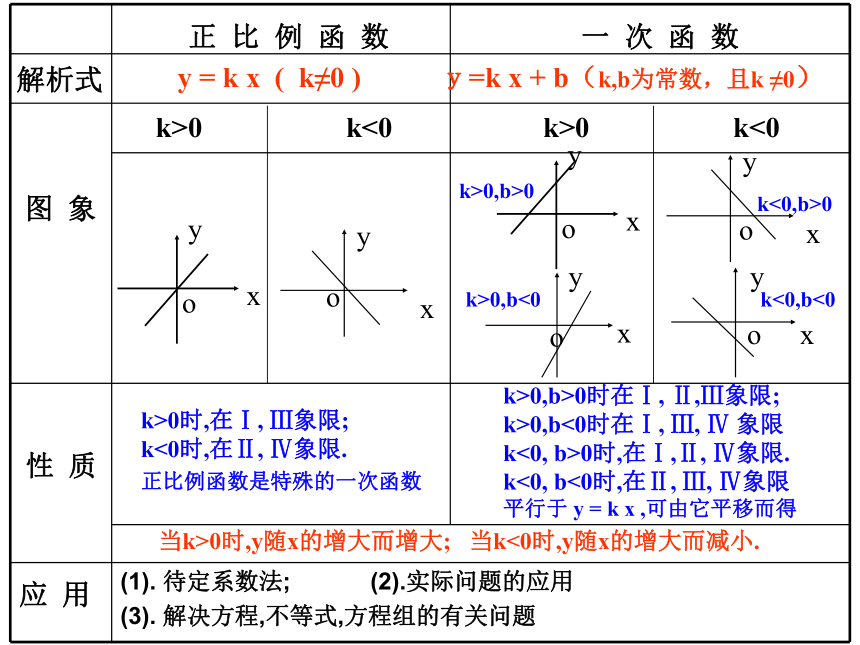
一 次 函 数
正 比 例 函 数
解析式
图 象
性 质
应 用
y = k x ( k≠0 ) ｙ=k x + b（k,b为常数，且k ≠0）
k>0　 k<0 k>0　 k<0
y
x
o
y
x
o
x
y
o
y
x
o
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
y
x
o
x
y
o
k>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数
k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得
当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
二、范例。
例１　填空题：
(1)　有下列函数：①　　　　　 , ②　　　　 ,
③　　　 , ④ 。其中过原点的直
线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象过第一、二、三象限的是_____。
②
①、②、③
④
③
　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么
k的值为________。
　　(3)、已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。
k=2
解：设一次函数解析式为y=kx+b，
把x=1时， y=5；x=6时，y=0代入解析式，得
解得
∴一次函数的解析式为　y= - x+6。
点评：用待定系数法求一次函数y=kx+b的解析式，可由已知条件给出的两对x、y的值，列出关于k、b的二元一次方程组。由此求出k、b的值，就可以得到所求的一次函数的解析式。
例２、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且
它的图象与x轴交点的横坐标是６，求这个一次函数的
解析式。
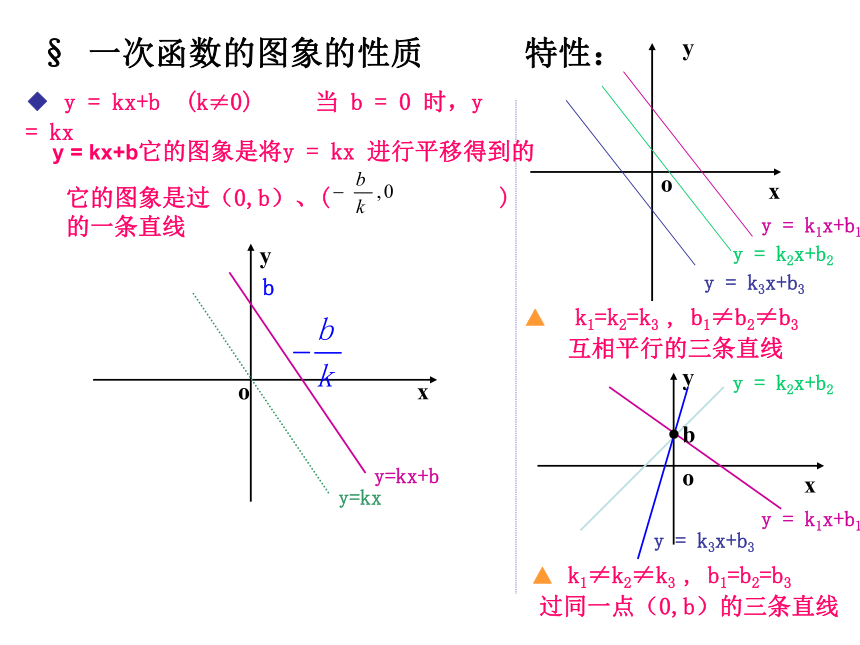
§ 一次函数的图象的性质
◆ y = kx+b (k≠0) 当 b = 0 时，y = kx
x
y
o
b
特性：
x
y
o
y = k1x+b1
y = k2x+b2
y = k3x+b3
▲ k1=k2=k3 , b1≠b2≠b3
互相平行的三条直线
x
y
o
y = k2x+b2
y = k3x+b3
b
●
▲ k1≠k2≠k3 , b1=b2=b3
过同一点（0,b）的三条直线
y=kx
y=kx+b
y = kx+b它的图象是将y = kx 进行平移得到的
y = k1x+b1
它的图象是过（0,b）、( ) 的一条直线
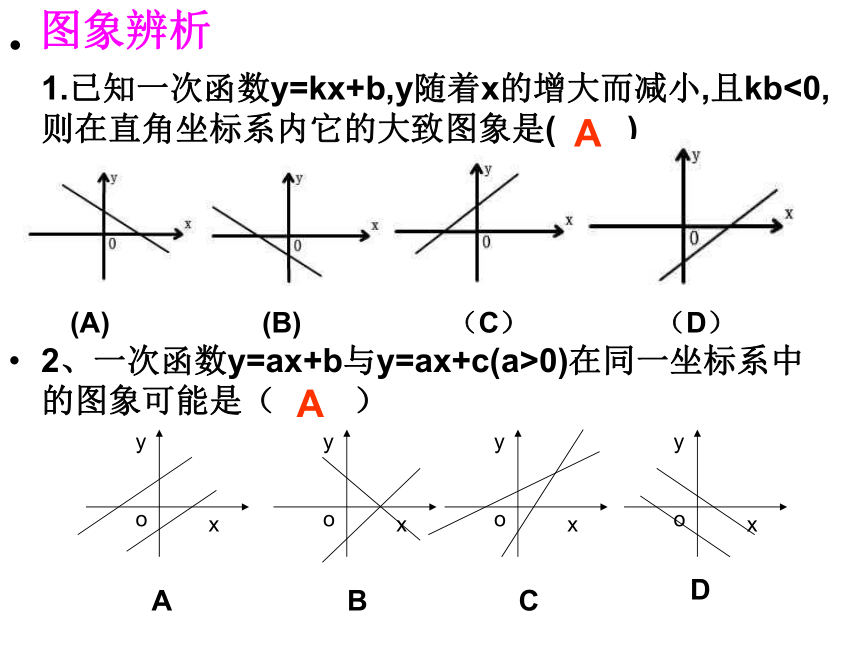
2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　)
　(A) 　　　　　(B) 　（C） 　　（D）
A
图象辨析
A
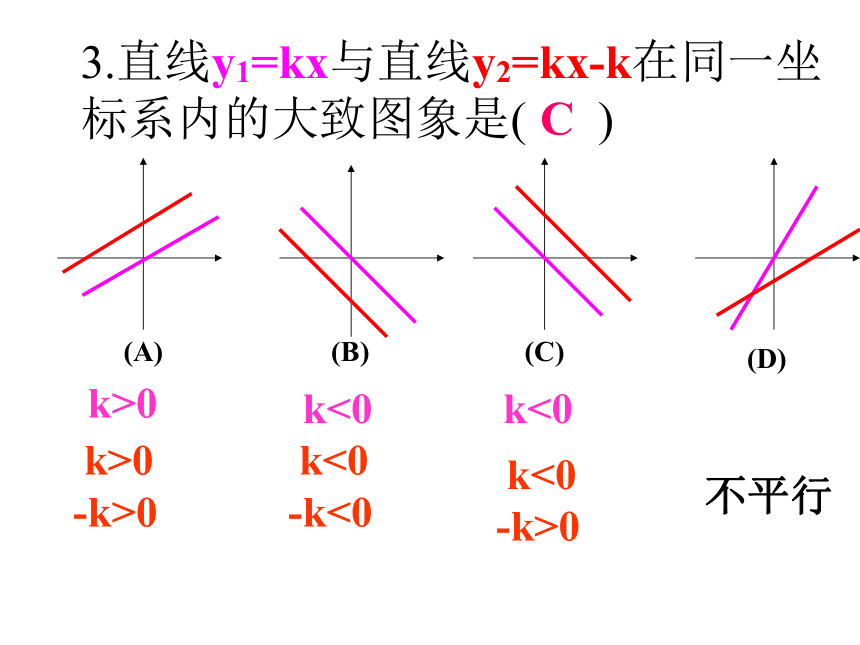
3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
(A)
(B)
(C)
(D)
C
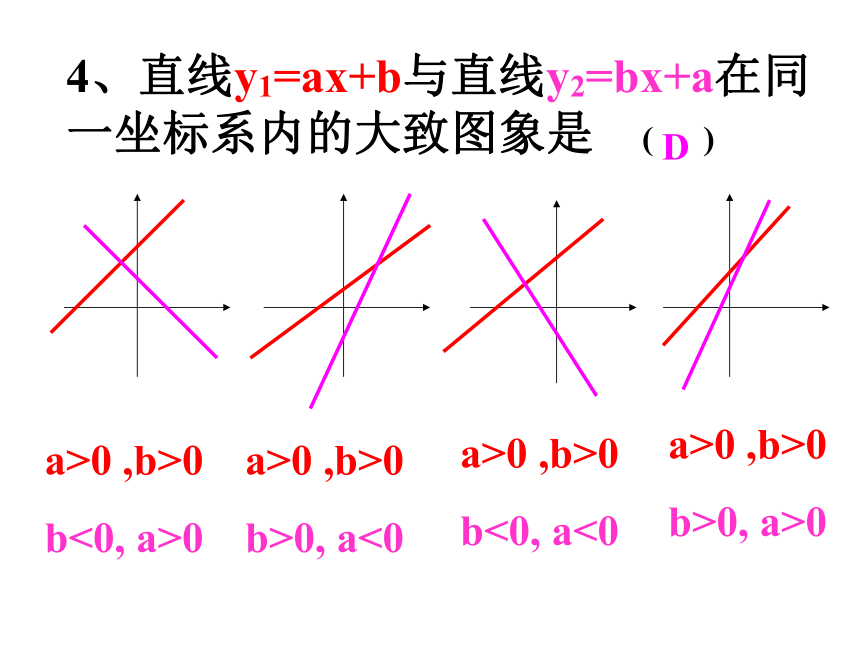
4、直线y1=ax+b与直线y2=bx+a在同一坐标系内的大致图象是　( )
a>0 ,b>0
b<0, a>0
a>0 ,b>0
b>0, a<0
a>0 ,b>0
b<0, a<0
a>0 ,b>0
b>0, a>0
D
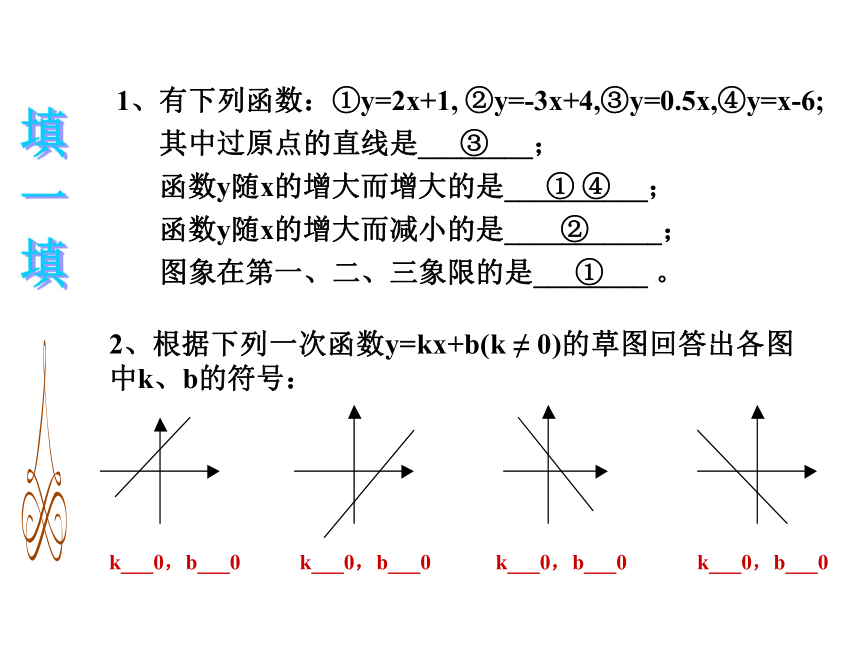
2、根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号：
k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0
1、有下列函数：①y=2x+1, ②y=-3x+4,③y=0.5x,④y=x-6;
① ④
②
③
①
函数y随x的增大而增大的是__________；
其中过原点的直线是________；
函数y随x的增大而减小的是___________；
图象在第一、二、三象限的是________ 。
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A
C
B
D
D
典型例题
函数平移
例1、将直线 向下平移3个单位后得到的直线是 。
直线平移：
向上平移b个单位
向下平移b个单位
1、直线 是由
向 平移 个单位得到的。
配套练习
函数平移
2、将直线 平移后经过点
(-4，-1)。
(1)求直线平移后的解析式；
(2)若直线是沿y轴平移的，则平移了几个单位长度？
(3)若直线是沿x轴平移的，则平移了几个单位长度？
配套练习
怎样了解左右平移的情况？
确定与x轴的交点坐标
函数平移
典型例题
观察函数图象
例2、如图，l1表示某摩托车厂一天的销售收入与销售量的关系；l2表示某摩托车厂一天的销售成本与销售量的关系。
(1)写出销售收入与销售量之间的函数关系式；
(2)写出销售成本
与销售量之间的
函数关系式；
根据不同变化关系求两个函数解析式
x
0
y
4
4
2
l2
l1
典型例题
例2、如图，l1表示某摩托车厂一天的销售收入与销售量的关系；l2表示某摩托车厂一天的销售成本与销售量的关系。
(3)当一天的销售量为多少时，销售收入等于成本？
(4)当一天的销售
量超过多少时，
工厂才获利？
根据图象观察所得
x
0
y
4
4
2
l2
l1
观察函数图象
配套练习
3、如图，l1、l2分别表示 一种白炽灯和
一种节能灯的费用(灯的售价和电费)y
(元)与照明时间x(h)的函数图象，假设两
种灯的使用寿命都是2000h，照明效果一
样。
(1)根据图象分别
求出l1、l2的函数
关系式；
观察函数图象
x
0
y
1000
17
2
l2
l1
20
26
500
配套练习
3、如图，l1、l2分别表示 一种白炽灯和
一种节能灯的费用(灯的售价和电费)y
(元)与照明时间x(h)的函数图象，假设两
种灯的使用寿命都是2000h，照明效果一
样。
(2)当照明时间为多
少小时时，两种灯
的使用寿命相等？
观察函数图象
x
0
y
1000
17
2
l2
l1
20
26
500
配套练习
3、如图，l1、l2分别表示 一种白炽灯和
一种节能灯的费用(灯的售价和电费)y
(元)与照明时间x(h)的函数图象，假设两
种灯的使用寿命都是2000h，照明效果一
样。
(3)小明的房间计划
照明2500h，他买了
一个白炽灯和一个
节能灯，请你帮他
设计最省钱的用灯方式。
观察函数图象
x
0
y
1000
17
2
l2
l1
20
26
500
典型例题
例3、从A、B两水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，A、B两地各可调出水14万吨。从A到甲地50千米，到乙地30千米；从B地到甲地60千米，到乙地45千米。设计一个调运方案使水的调运量(单位：万吨·千米)最小。
方案设计问题
怎样确定自变量取值范围？
4、某运输公司根据需要，计划构进大、
中型客车共10辆，大型客车每辆价格25万元，中型客车每辆价格15万元。
(1)若设购买大型客车x辆，购车总费用
为y万元，求y与x之间的函数解析式；
(2)若购车资金为180至200万元(含180和200万元)，在确保交通安全的前提下，
根据客流量的调查结果，大型客车应不少于4辆，此时如何确定购车方案可使运输该公司购车费用最少？
配套练习
方案设计问题
典型例题
例3、A、B两个商场平时以同样的价格出售相同的商品，在春节期间让利酬宾，A商场所有的商品8折出售；B商场消费金额超过200元后，可在这家商场7折购物。试问如何选择商场来购物更经济？
方案选择问题
列两个函数式
用不等式(方程)
分类讨论
典型例题
确定三角形的面积
例4、求一次函数 的图象与
两轴围成的三角形的面积。
与两轴的交点坐标
三角形是边长
配套练习
5、已知一个正比例函数和一个一次
函数，它们的图象都经过点P(-2，1)，
且一次函数的图象与x轴交于点Q(3，0)。
(1)求这两个函数的解析式；
(2)求出△POQ的面积。
待定系数法
给出点坐标
确定三角形的面积
y/毫安
x/天
此种手机的电板最大带电量是多少？
1、某手机的电板剩余电量y毫安是使用天数x的一次函数x和y关系如图 ：
我 能 行
小 试 牛 刀
2、某植物t天后的高度为ycm,图中反映了y与t之间的关系，根据图象回答下列问题：
(1)植物刚栽的时候多高？
9
6
3
12
15
18
21
24
l
2
4
6
8
10
12
14
t/天
Y cm
（2）3天后该植物高度为多少？
（3）几天后该植物高度可达21cm
（4）先写出y与t的关系式，
再计算长到100cm需几天？
小试 牛刀
初生牛犊不怕虎
3、 某地长途汽车客运公司规定旅客可随身携带一定质量的行李，如果超过规定，则需要购买行李票，行李票费用y元与行李质量的关系如图：
旅客最多可免费携带多少千克行李？
⑵超过30千克后，每千克需付多少元？
⑴想一想紫红色那段图象表示什么意思？
生活中的数学
做 一 做

4、 下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。
做一做
新龟兔赛跑
s /米
（1）这一次是 　米赛跑。
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
（2）表示兔子的图象是 。
-1
12
9
10
11
-3
-2
l1
l2
100
l2
-4
根据图象可以知道：
s /米
（3）当兔子到达终点时，乌龟距终点还有 　米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
（4）乌龟要与兔子同时到达终点乌龟要先跑 米。
（5）乌龟要先到达终点，至少要比兔子早跑 分钟。
-1
12
9
10
11
-3
-2
40
4
-4
你还能用其他方法解决上述问题吗？
40
是哪个队获胜了？
5、10千米龙舟比赛中，红队由于某些原因，晚出发了。出发时蓝队已经划出了 500米，如图所示， 和m分别表示蓝队和红队的行驶路程y（千米）和时间x（分）之间的关系。
y(千米)
x(分)
m
2
4
6
8
5
10
15
20
25
0

6、已知：函数y = (m+1) x+2 m﹣6
（1）若函数图象过（﹣1 ，2），求此函数的解析式。
（2）若函数图象与直线 y = 2 x + 5 平行，求其函数的解析式。
（3）求满足（2）条件的直线与此同时y = ﹣3 x + 1 的交点
并求这两条直线 与y 轴所围成的三角形面积
解：（1）由题意:
2=﹣(m+1）+2m﹣6
解得 m = 9
∴ y = 10x+12
(2) 由题意，m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
解得: x =1 , y = ﹣2
∴ 这两直线的交点是（1 ，﹣2）
y = 2x﹣4 与y 轴交于( 0 , 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1）
●
x
y
o
1
1
﹣4
(1, ﹣2)
S△=
-2
小明在电信局办理了某种电话话费套餐，该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费，办理后某月手机话费y元和通话时间x的关系图如下：
观察图象形状,有何特点，你知道该电话套餐的内容吗？
⑴该话费套餐的月租费是多少元
⑵每分钟通话需多少元
100分钟后每分钟通话：
100分钟前每分钟通话：
思考：