第六章 图形与坐标复习

(共20张PPT)
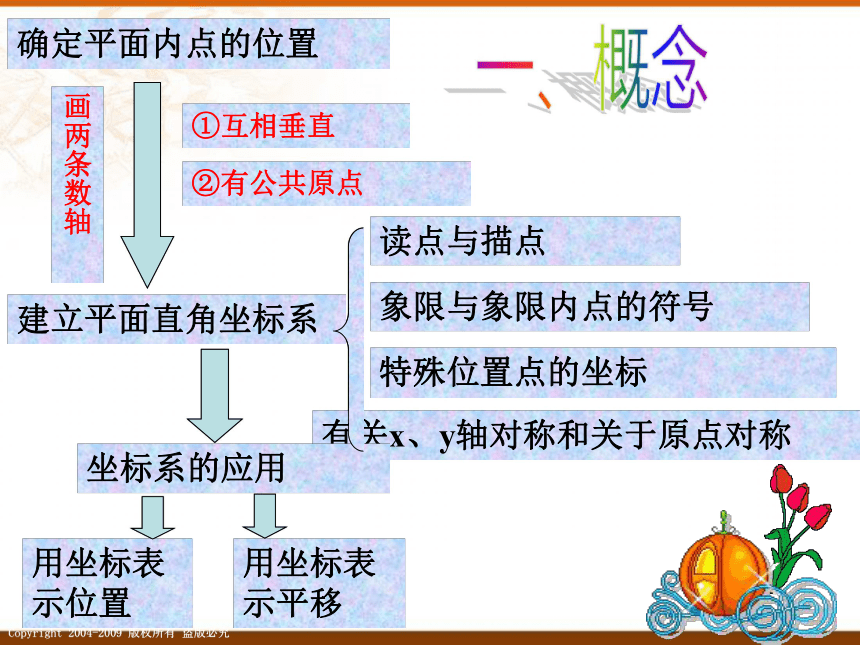
确定平面内点的位置
①互相垂直
②有公共原点
建立平面直角坐标系
读点与描点
象限与象限内点的符号
特殊位置点的坐标
有关x、y轴对称和关于原点对称
坐标系的应用
用坐标表示位置
用坐标表示平移
画两条数轴
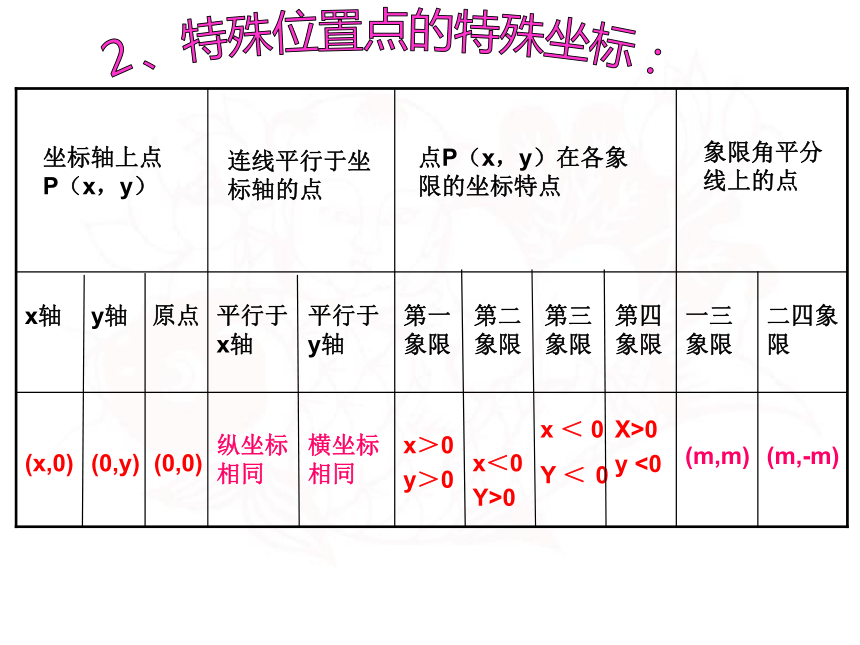
(m,-m)
(m,m)
x＜0
Y>0
X>0
y <0
x ＜ 0
Y ＜ 0
x＞0
y＞0
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
二四象限
一三象限
第四象限
第三象限
第二象限
第一象限
平行于y轴
平行于x轴
原点
y轴
x轴
象限角平分线上的点
点P（x，y）在各象限的坐标特点
连线平行于坐标轴的点
坐标轴上点P（x，y）
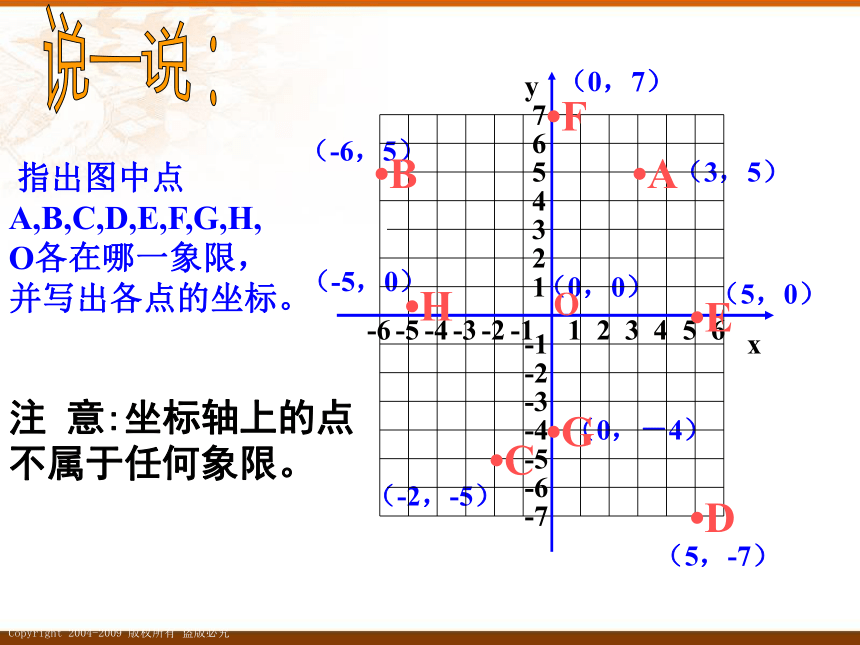
指出图中点A,B,C,D,E,F,G,H,O各在哪一象限，并写出各点的坐标。
（3，5）
（0，－4）
（-2，-5）
（-5，0）
（-6，5）
（0，7）
（5，0）
（0，0）
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
O
y
x
G
B
F
A
C
D
E
H
（5，-7）
注 意:坐标轴上的点不属于任何象限。
0
1
-1
1
-1
x
y
（x，０）
（０，y）
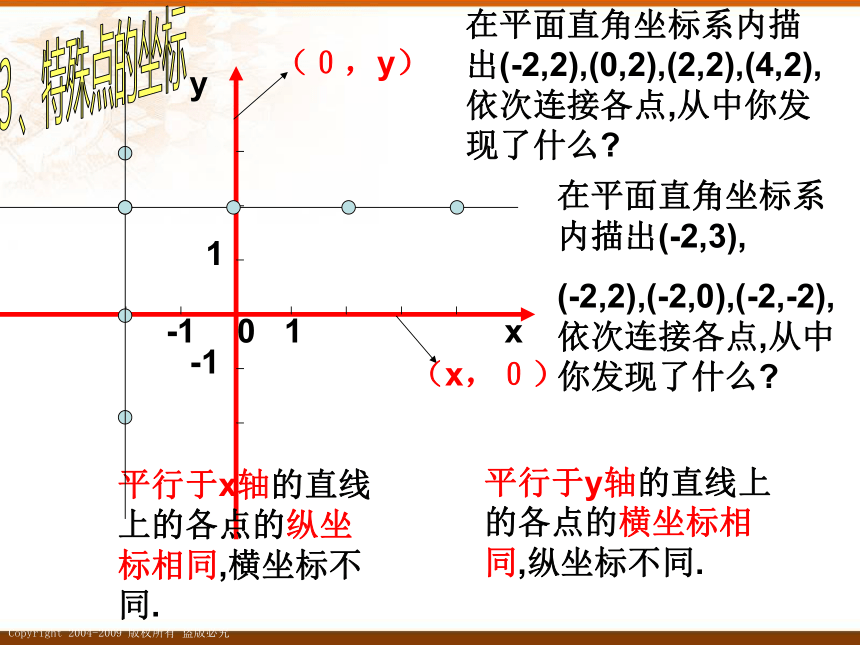
在平面直角坐标系内描出(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么
平行于x轴的直线上的各点的纵坐标相同,横坐标不同.
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
在平面直角坐标系内描出(-2,3),
(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么
0
1
-1
1
-1
x
y
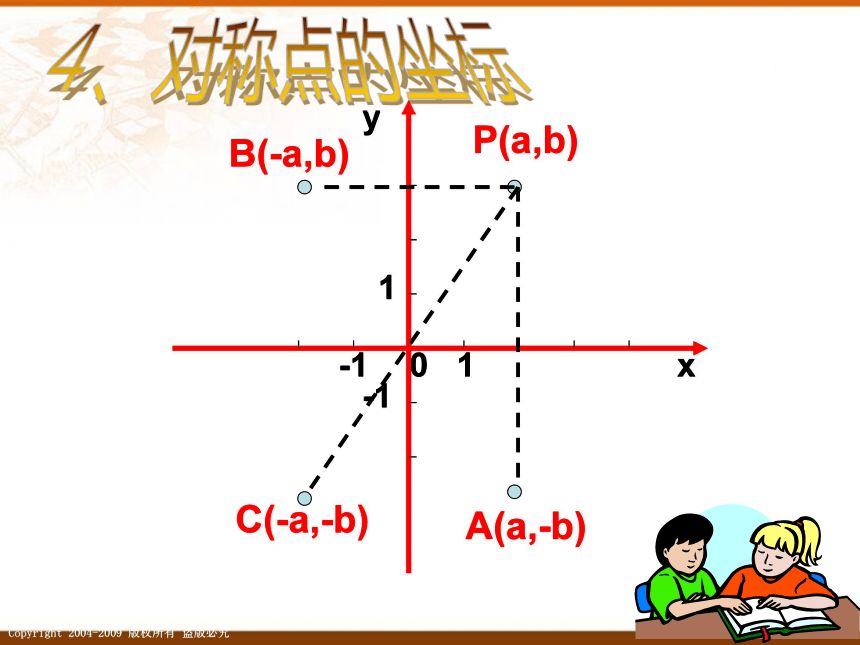
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
1.小明位于广场的北偏西30°方向上，距离广场3 千米，则广场的位置是在小明的＿＿＿＿＿＿＿＿＿＿＿＿
２．若点Ａ的坐标是（－３，５），则它到
x轴的距离是＿＿，到y轴的距离是＿＿＿＿　
４．点Ｐ到x轴、y轴的距离分别是２、１，
则点Ｐ的坐标可能为＿＿＿＿＿＿＿＿＿＿＿　　　　　
３．若点Ｂ在x轴下方，y轴左侧，并且到
x轴、y轴距离分别是２、４个单位长度，
则点Ｂ的坐标是＿＿＿＿＿
（-4，-2）
(1,2)、(1,-2)、(-1,2)、(-1,-2)
南偏东30°，
　5
3
距小明3千米
1.点Ｐ的坐标是（２，－３），则点Ｐ在第　　　象限．
２．若点Ｐ（x，y）的坐标满足xy﹥０，则点Ｐ　　　　在第　　　　　　　　象限；
3.若点Ｐ（x，y）的坐标满足xy﹤０，且在x轴上方，则点Ｐ在第　　　象限．
4、点P（x，y）在第四象限，且|x|=3，|y|=2，则P点的坐标是　　　　　　
　　　　　　　　　　　　　　　
四
一或三
二
二、坐标与象限的关系或坐标轴关系
5、点P（a-1，a2-9）在x轴负半轴上，
则P点坐标是　　　　　。
(3，-2）
（-4，0）
三、平行线在坐标轴中的应用
1、已知点A（m，-2），点B（3，m-1），且直线AB∥x轴，则m的值为 。
2、把以（-3，7），（-3，-2）为端点的线段向左平移5个单位，所得像上任意一点的坐标可表示为
3、把平行与X轴的直线（x,-3)向上移动2个单位得到
4、已知长方形在平面直角坐标系中三个顶点坐标是（-3，-3），（-3，6），（5，6），求第四个顶点的坐标
四、平移规律解题
1、三角形ABC三个顶点A、B、C的坐标分别为
A（2，-1），B（1，-3），C（4，-3.5）。
把三角形A1B1C1向右平移4个单位，再向下平移3个单位，恰好得到三角形ABC，试写出三角形A1B1C1三个顶点
2、在直角坐标系中，把点P（a,b）先向左平移3个单位，再向上平移2个单位，再把所得的点以x轴作轴对称变换，最终所得的像为点（5，4），求点P的坐标。
五、面积和长度的计算
1、三角形ABC三个顶点A、B、C的坐标分别为A（2，-1），B（1，-3），C（4，-5）
（1）求三角形ABC的面积
（2）求三角形的三边长，判断三角形形状
2、把A(a,-3)点向左平移3个单位，所得的像
与点A关于y轴对称, 求a的值。
1.点（3，-2）在第_____象限;点（-1.5，-1）在第_______象限；点（0，3）在____轴上；若点（a+1，-5）在y轴上，则a=______.
4.若点P在第三象限且到x轴的距离为 2 ，
到y轴的距离为1.5，则点P的坐标是________。
3.点 M（- 8，12）到 x轴的距离是_________，
到 y轴的距离是________.
2.点A在x轴上，距离原点4个单位长度，则A点的坐标是 ____________。
四
三
y
-1
(4,0)或(-4,0)
12
8
（-1.5，-2）
6.如果同一直角坐标系下两个点的横坐标相同，那么过这两点的直线（ ） （A）平行于x轴 （B）平行于y轴
（C）经过原点 （D）以上都不对
7.若点（a,b-1)在第二象限，则a的取值范围是_____，b的取值范围________。
5.在平面直角坐标系内,已知点P ( a , b ),
且a b < 0 , 则点P的位置在____________。
第二或四象限
B
a<0
b>1
8.点A（1-a，5），B（3 ,b）关于y轴对称，则a=___,b=____。
5
4
10、点（4，3）与点（4，- 3）的关系是【 】. （A）关于原点对称 （B）关于 x轴对称 （C）关于 y轴对称 （D）不能构成对称关系
9.实数 x，y满足 (x-1)2+ |y| = 0，则点 P（ x，y）在【 】. （A）原点 （B）x轴正半轴
（C）第一象限 （D）任意位置
B
C
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
.
.
A
B
11、方格纸上B、A两点，如图所示，若以B点为原点，建立直角坐标系，则A点坐标为（3，4），若以A点为原点建立直角坐标系，则B点坐标为 。
　　　这节课你有何收获，
能与大家分享、交流你的感受吗？
1、位置确定的方法
（1）坐标定位
（2）方向定位
（3）区域定位
2、平面直角坐标系
定义
概念
坐标特点
坐标确定
布置作业:
见数学作业本