三角形的内切圆
图片预览

文档简介
(共13张PPT)
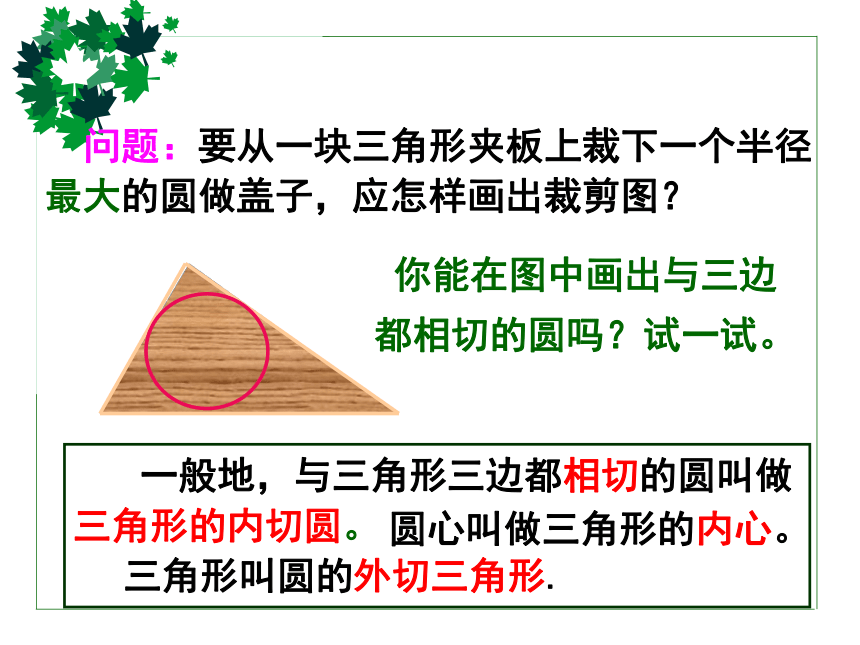
问题:要从一块三角形夹板上裁下一个半径最大的圆做盖子,应怎样画出裁剪图?
你能在图中画出与三边都相切的圆吗?试一试。
一般地,与三角形三边都相切的圆叫做三角形的内切圆。
三角形叫圆的外切三角形.
圆心叫做三角形的内心。
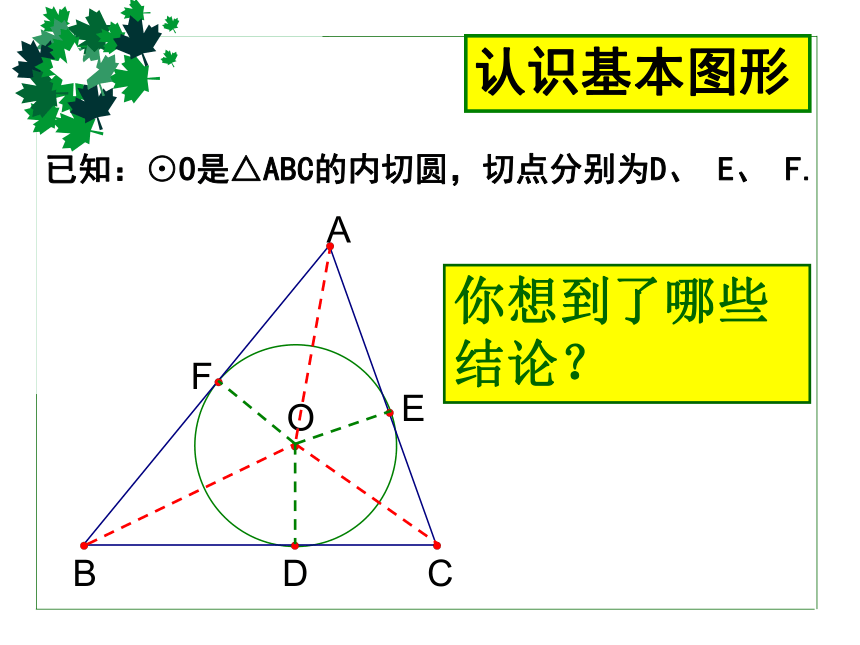
认识基本图形
你想到了哪些结论?
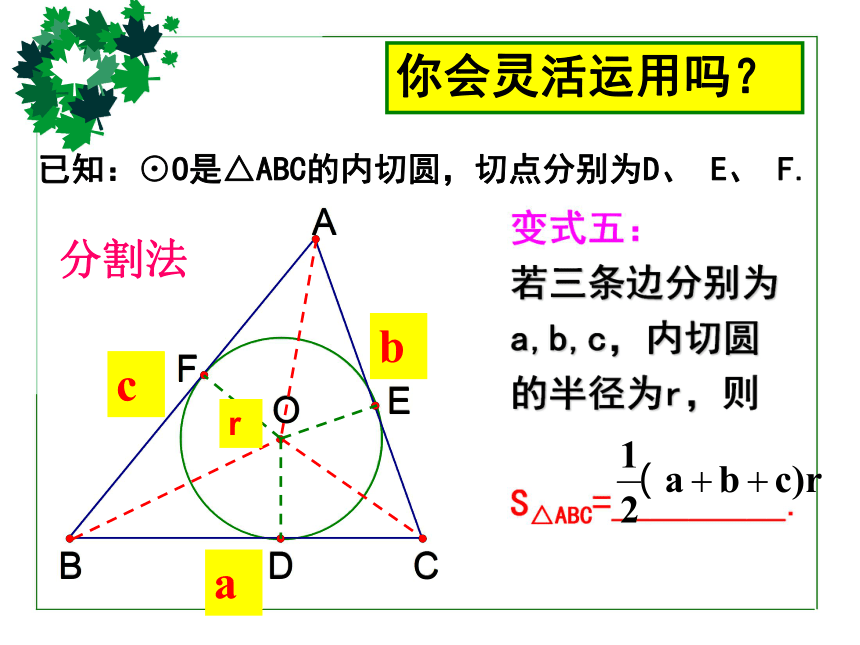
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
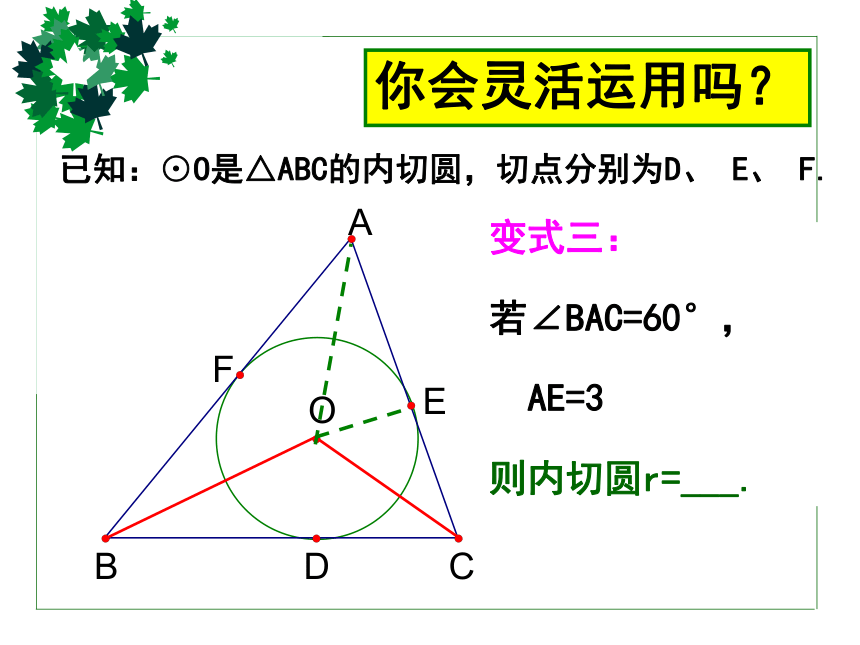
你会灵活运用吗?
思考:
若∠ABC=50°,∠ACB=70°,
则∠BOC=___ °.
变式一:
若∠BAC=60°,
则∠BOC=___ °.
变式二:
∠BAC=n°,
则∠BOC=___ °.
变式三:
若∠BAC=60°,
AE=3
则内切圆r=___.
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
2
3
4
证明:连接OD,OE,OC
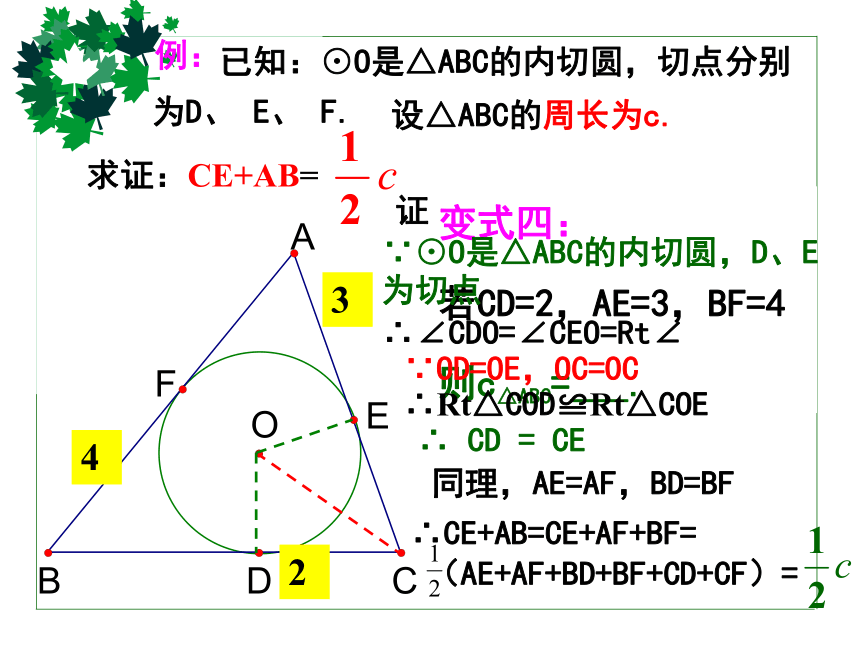
变式四:
若CD=2,AE=3,BF=4
则c△ABC=___.
例:
设△ABC的周长为c.
求证:CE+AB=
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
∵⊙O是△ABC的内切圆,D、E为切点
∴∠CDO=∠CEO=Rt∠
∵OD=OE,OC=OC
∴Rt△COD≌Rt△COE
∴ CD = CE
同理,AE=AF,BD=BF
∴CE+AB=CE+AF+BF=
(AE+AF+BD+BF+CD+CF)=
变式五:
若三条边分别为a,b,c,内切圆的半径为r,则
S△ABC=_________.
分割法
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
r
a
b
c
你会灵活运用吗?
C
B
A
D
E
F
O
r
a
b
c
你还认识吗?
四边形OECD是正方形
已知⊙O是Rt△ABC的内切圆,切点分别为D、E、F,∠ACB=Rt∠.
⊙O
△ABC
圆心
画法
性质
△ABC的外接圆
⊙O的内接三角形
三角形的外心
中垂线的交点
△ABC的内切圆
⊙O的外切三角形
三角形的内心
角平分线的交点
到三边的距离相等
到三个顶点的距离相等
你记得吗?
图形
项目
A
B
C
. O
A
B
C
. O
一个概念
一个基本图形
一种求面积的方法
梳 理
三角形的内切圆
分割法
A层:作业本,同步练习;
B层:作业本,同步练习(课前准备、
课堂检测);
C层:作业本,教材P59作业1、2、3、5
作业布置
小虎同学在作三角形内切圆时,三角形的内心找到了,但他画了的圆和三边都相交,他惊奇地发现:⊙O在三边相截的三条线段长相等。你认为他的发现的结论正确吗?请说明理由。
延 伸
C
B
A
D
E
F
O
你还会用我吗?
G
变 式:
若AO的延长线与BC交于点G,AC=6,CG=2,试求⊙O的半径.
问题:要从一块三角形夹板上裁下一个半径最大的圆做盖子,应怎样画出裁剪图?
你能在图中画出与三边都相切的圆吗?试一试。
一般地,与三角形三边都相切的圆叫做三角形的内切圆。
三角形叫圆的外切三角形.
圆心叫做三角形的内心。
认识基本图形
你想到了哪些结论?
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
你会灵活运用吗?
思考:
若∠ABC=50°,∠ACB=70°,
则∠BOC=___ °.
变式一:
若∠BAC=60°,
则∠BOC=___ °.
变式二:
∠BAC=n°,
则∠BOC=___ °.
变式三:
若∠BAC=60°,
AE=3
则内切圆r=___.
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
2
3
4
证明:连接OD,OE,OC
变式四:
若CD=2,AE=3,BF=4
则c△ABC=___.
例:
设△ABC的周长为c.
求证:CE+AB=
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
∵⊙O是△ABC的内切圆,D、E为切点
∴∠CDO=∠CEO=Rt∠
∵OD=OE,OC=OC
∴Rt△COD≌Rt△COE
∴ CD = CE
同理,AE=AF,BD=BF
∴CE+AB=CE+AF+BF=
(AE+AF+BD+BF+CD+CF)=
变式五:
若三条边分别为a,b,c,内切圆的半径为r,则
S△ABC=_________.
分割法
已知:⊙O是△ABC的内切圆,切点分别为D、 E、 F.
r
a
b
c
你会灵活运用吗?
C
B
A
D
E
F
O
r
a
b
c
你还认识吗?
四边形OECD是正方形
已知⊙O是Rt△ABC的内切圆,切点分别为D、E、F,∠ACB=Rt∠.
⊙O
△ABC
圆心
画法
性质
△ABC的外接圆
⊙O的内接三角形
三角形的外心
中垂线的交点
△ABC的内切圆
⊙O的外切三角形
三角形的内心
角平分线的交点
到三边的距离相等
到三个顶点的距离相等
你记得吗?
图形
项目
A
B
C
. O
A
B
C
. O
一个概念
一个基本图形
一种求面积的方法
梳 理
三角形的内切圆
分割法
A层:作业本,同步练习;
B层:作业本,同步练习(课前准备、
课堂检测);
C层:作业本,教材P59作业1、2、3、5
作业布置
小虎同学在作三角形内切圆时,三角形的内心找到了,但他画了的圆和三边都相交,他惊奇地发现:⊙O在三边相截的三条线段长相等。你认为他的发现的结论正确吗?请说明理由。
延 伸
C
B
A
D
E
F
O
你还会用我吗?
G
变 式:
若AO的延长线与BC交于点G,AC=6,CG=2,试求⊙O的半径.
