2021-2022学年浙教版九年级上第3章 圆的基本性质单元测试(1)(含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级上第3章 圆的基本性质单元测试(1)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 13:53:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级上第3章 圆的基本性质单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2021 婺城区校级开学)若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
2.(2021 兴化市模拟)若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. B.3π C.6π D.9π
3.(2021 阜新)如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
4.(2020秋 巩义市期末)如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
5.(2021秋 江阴市期中)有下列说法:①任意三点确定一个圆;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
6.(2021 拱墅区二模)如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m B.m C.5m D.m
7.(2021 越秀区校级四模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=56°,则∠AOC的度数为( )
A.56° B.124° C.112° D.146°
8.(2021 眉山)如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
9.(2021 安徽模拟)如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
10.(2020春 海淀区校级月考)如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
二.填空题(共6小题,每小题4分,共24分)
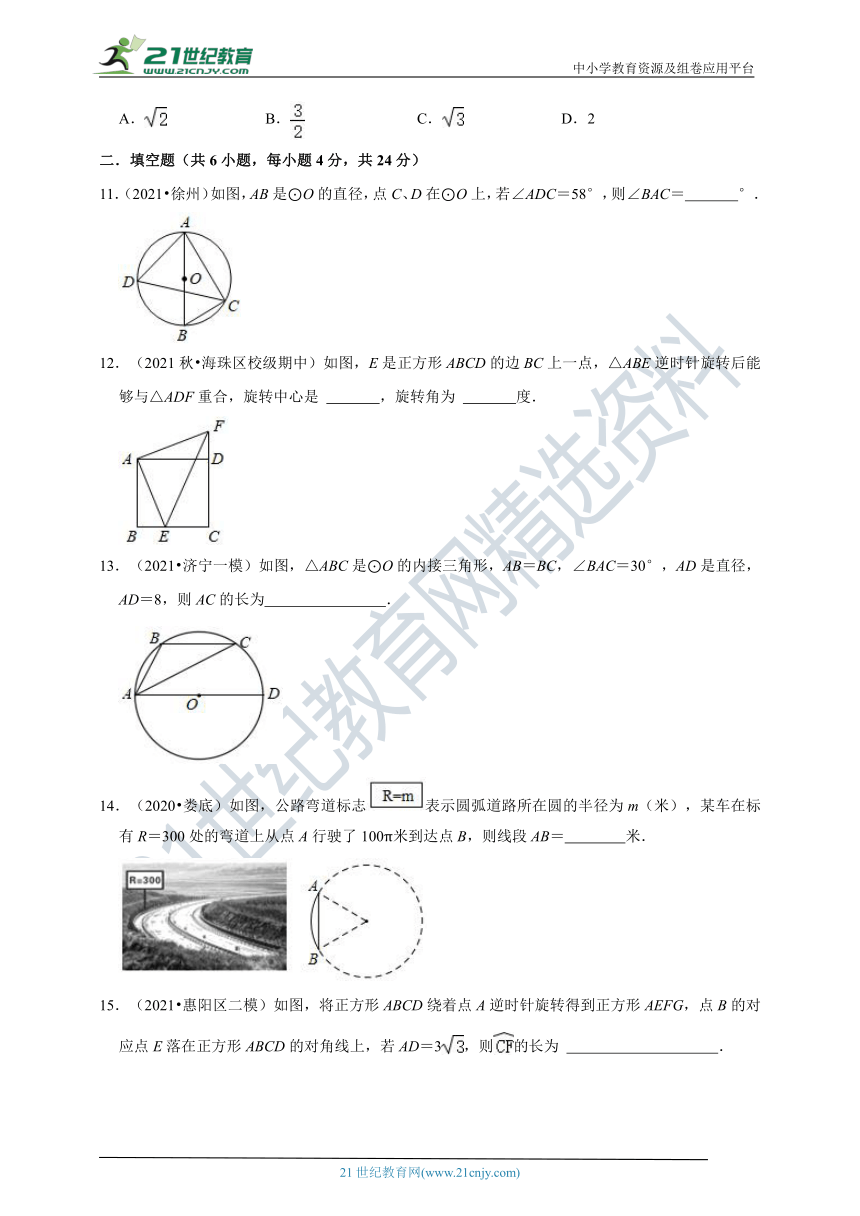
11.(2021 徐州)如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= °.
12.(2021秋 海珠区校级期中)如图,E是正方形ABCD的边BC上一点,△ABE逆时针旋转后能够与△ADF重合,旋转中心是 ,旋转角为 度.
13.(2021 济宁一模)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为 .
14.(2020 娄底)如图,公路弯道标志表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B,则线段AB= 米.
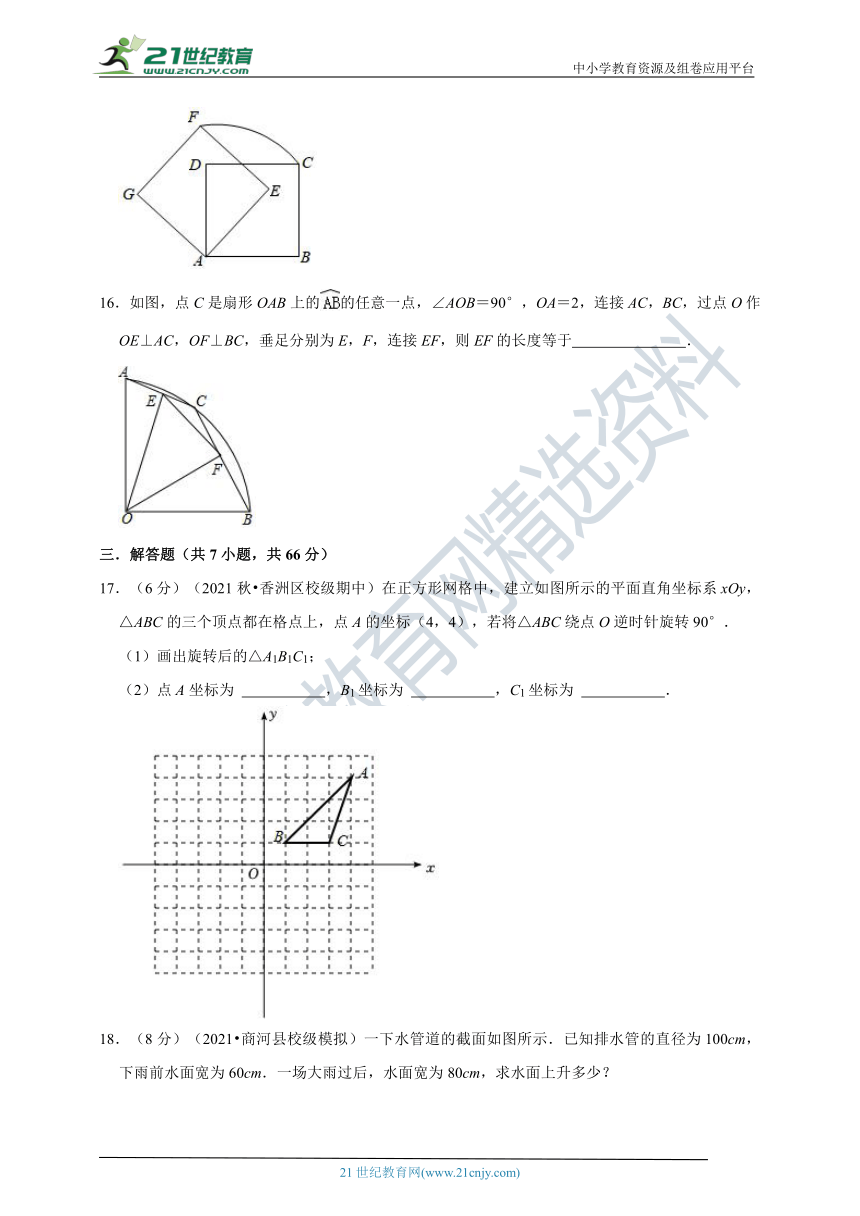
15.(2021 惠阳区二模)如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,若AD=3,则的长为 .
16.如图,点C是扇形OAB上的的任意一点,∠AOB=90°,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 香洲区校级期中)在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),若将△ABC绕点O逆时针旋转90°.
(1)画出旋转后的△A1B1C1;
(2)点A坐标为 ,B1坐标为 ,C1坐标为 .
18.(8分)(2021 商河县校级模拟)一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
19.(8分)(2021 徐州)如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
20.(10分)(2021春 永嘉县校级期末)如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
21.(10分)(2020秋 拱墅区校级期中)如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
22.(12分)(2020秋 红谷滩区校级期末)如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8,求:
①⊙O的半径;
②求图中阴影部分的面积.
23.(12分)已知:⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
(1)如图1,若AC⊥BD,点O到AD的距离为a,求证:BC=2a;
(2)如图2,若=,AD是⊙O的直径,AD=25,CD=7,求四边形ABCD的面积.
答案与解析
一.选择题
1.(2021 婺城区校级开学)若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
【解析】解:∵AP=2<5,
∴点P在⊙A内部.
故选:C.
2.(2021 兴化市模拟)若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. B.3π C.6π D.9π
【解析】解:S扇形==9π,
故选:D.
3.(2021 阜新)如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
【解析】解:∵∠AOB和∠C都对,
∴∠C=∠AOB=×70°=35°.
故选:B.
4.(2020秋 巩义市期末)如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
【解析】解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
5.(2021秋 江阴市期中)有下列说法:①任意三点确定一个圆;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
【解析】解:①不在同一直线上的三点确定一个圆,本说法错误;
②任意一个三角形有且仅有一个外接圆,本说法正确;
③长度相等的两条弧不一定是等弧,本说法错误;
④直径是圆中最长的弦,本说法正确;
故选:D.
6.(2021 拱墅区二模)如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m B.m C.5m D.m
【解析】解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=2(m),
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+22=OB2,
解得:OB=(m),
即这个轮子的半径长为m,
故选:D.
7.(2021 越秀区校级四模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=56°,则∠AOC的度数为( )
A.56° B.124° C.112° D.146°
【解析】解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,∠CBE=56°,
∴∠ADC=∠CBE=56°,
由圆周角定理得:∠AOC=2∠ADC=112°,
故选:C.
8.(2021 眉山)如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
【解析】解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵=3,
∴∠CAB=3∠ABC,
∴∠ABC=22.5°,∠CAB=67.5°,
∵CD⊥AB,
∴∠ACE=22.5°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=22.5°,
∵∠CAF=∠CBF,
∴∠CBF=22.5°,
故选:C.
9.(2021 安徽模拟)如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
【解析】解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
10.(2020春 海淀区校级月考)如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
【解析】解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r sin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
二.填空题
11.(2021 徐州)如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= 32 °.
【解析】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=∠ADC=58°,
∴∠BAC=90°﹣∠B=32°.
故答案为32.
12.(2021秋 海珠区校级期中)如图,E是正方形ABCD的边BC上一点,△ABE逆时针旋转后能够与△ADF重合,旋转中心是 点A ,旋转角为 90 度.
【解析】解:从图形和已知可知:旋转中心是点A,旋转角的度数等于∠BAD的度数,即为90°,
故答案为:点A;90.
13.(2021 济宁一模)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为 4 .
【解析】解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC==4,
故答案为:4.
14.(2020 娄底)如图,公路弯道标志表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B,则线段AB= 300 米.
【解析】解:设线段AB对应的圆心角度数为n,
∵100π==,
∴n=60°,
又AO=BO,
∴△AOB是等边三角形,
∴AB=AO=BO=300(米),
故答案为:300.
15.(2021 惠阳区二模)如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,若AD=3,则的长为 .
【解析】解:连接AC,AF,
∵四边形ABCD是正方形,
∴∠DAC=45°,AD=DC=3,∠ADC=90°,
由勾股定理得:AC===3,
∵将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,
∴A、D、F三点共线,A、E、C三点共线,
∴∠FAC=45°,
∴的长是=,
故答案为:.
16.如图,点C是扇形OAB上的的任意一点,∠AOB=90°,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
【解析】解:连接AB,如图,
∵OE⊥AC,OF⊥BC,
∴AE=CE,BF=CF,
∴EF为△CAB的中位线,
∴EF=AB,
∵∠AOB=90°,OA=OB,
∴AB=OA=2,
∴EF=.
故答案为.
三.解答题
17.(2021秋 香洲区校级期中)在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),若将△ABC绕点O逆时针旋转90°.
(1)画出旋转后的△A1B1C1;
(2)点A坐标为 (﹣4,4) ,B1坐标为 (﹣1,1) ,C1坐标为 (﹣1,3) .
【解析】解:(1)如图△A1B1C1即为所求;
(2)点A1坐标为(﹣4,4),B1坐标为(﹣1,1),C1坐标为(﹣1,3).
故答案为:(﹣4,4),(﹣1,1),(﹣1,3).
18.(2021 商河县校级模拟)一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
【解析】解:作半径OD⊥AB交AB于C,连接OB,如图所示,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下,水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
19.(2021 徐州)如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
【解析】证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
20.(2021春 永嘉县校级期末)如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
【解析】(1)证明:∵C是的中点,
∴=,
∴∠ABC=∠CBD,点F是AD的中点,
∵OB=OC,
∴∠ABC=∠C,
∴∠ABC=∠CBD=∠C,
∴∠ABD=∠ABC+CBD=2∠C;
(2)解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC==6,
∵C是的中点,
∴OC⊥AD,
∴OA2﹣OF2=AF2=AC2﹣CF2,
∴52﹣OF2=62﹣(5﹣OF)2,
∴OF=1.4,
又∵O是AB的中点,F是AD的中点,
∴OF是△ABD的中位线,
∴BD=2OF=2.8.
21.(2020秋 拱墅区校级期中)如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
【解析】解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
22.(2020秋 红谷滩区校级期末)如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8,求:
①⊙O的半径;
②求图中阴影部分的面积.
【解析】(1)证明:∵AB 为⊙O 的直径,AB⊥CD,
∴BC=BD,
∴∠A=∠DCB,
∴OF⊥AC,
∴∠AFO=∠CEB,
∵BE=OF,
∴△AFO≌△CEB(AAS).
(2)①∵AB 为⊙O 的直径,AB⊥CD,
∴CE=CD=4
设 OC=r,则 OE=r﹣4,
∴r2=(r﹣4)2+(4)2
∴r=8.
②连接 OD.
∵OE=4=OC,
∴∠OCE=30°,∠COB=60°,
∴∠COD=120°,
∵△AFO≌△CEB,
∴S△AFO=S△BCE,
∴S阴=S扇形OCD﹣S△OCD
=﹣××4
=π﹣16
23.已知:⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
(1)如图1,若AC⊥BD,点O到AD的距离为a,求证:BC=2a;
(2)如图2,若=,AD是⊙O的直径,AD=25,CD=7,求四边形ABCD的面积.
【解析】(1)证明:如图1中,作直径AF,连接DF,过点O作OG⊥AD于G.
∵AF是直径,
∴∠ADF=90°,
∴∠DAF+∠F=90°,
∵BD⊥AC,
∴∠CAB+∠ABD=90°,
∵∠ABD=∠F,
∴∠FAD=∠CAB,
∴=,
∴BC=DF,
∵OG⊥AD,
∴AG=DG,
∵AO=OF,
∴DF=2OG=2a,
∴BC=2a.
(2)解:如图2中,连接OB交AC于点Q.
∵=,
∴OB⊥AC,
∴AQ=CQ,
∵AO=OD,
∴OQ=CD=,
∵AD是直径,
∴∠ACD=90°,
∴AD===25,
∴OB=AD=,
∴BQ=OB﹣OQ=9,
∴S四边形ABCD=S△ACD+S△ABC=×AC×CD+×AC×BQ=×7×24+×24×9=192.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级上第3章 圆的基本性质单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2021 婺城区校级开学)若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
2.(2021 兴化市模拟)若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. B.3π C.6π D.9π
3.(2021 阜新)如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
4.(2020秋 巩义市期末)如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
5.(2021秋 江阴市期中)有下列说法:①任意三点确定一个圆;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
6.(2021 拱墅区二模)如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m B.m C.5m D.m
7.(2021 越秀区校级四模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=56°,则∠AOC的度数为( )
A.56° B.124° C.112° D.146°
8.(2021 眉山)如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
9.(2021 安徽模拟)如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
10.(2020春 海淀区校级月考)如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
二.填空题(共6小题,每小题4分,共24分)
11.(2021 徐州)如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= °.
12.(2021秋 海珠区校级期中)如图,E是正方形ABCD的边BC上一点,△ABE逆时针旋转后能够与△ADF重合,旋转中心是 ,旋转角为 度.
13.(2021 济宁一模)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为 .
14.(2020 娄底)如图,公路弯道标志表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B,则线段AB= 米.
15.(2021 惠阳区二模)如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,若AD=3,则的长为 .
16.如图,点C是扇形OAB上的的任意一点,∠AOB=90°,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 香洲区校级期中)在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),若将△ABC绕点O逆时针旋转90°.
(1)画出旋转后的△A1B1C1;
(2)点A坐标为 ,B1坐标为 ,C1坐标为 .
18.(8分)(2021 商河县校级模拟)一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
19.(8分)(2021 徐州)如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
20.(10分)(2021春 永嘉县校级期末)如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
21.(10分)(2020秋 拱墅区校级期中)如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
22.(12分)(2020秋 红谷滩区校级期末)如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8,求:
①⊙O的半径;
②求图中阴影部分的面积.
23.(12分)已知:⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
(1)如图1,若AC⊥BD,点O到AD的距离为a,求证:BC=2a;
(2)如图2,若=,AD是⊙O的直径,AD=25,CD=7,求四边形ABCD的面积.
答案与解析
一.选择题
1.(2021 婺城区校级开学)若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
【解析】解:∵AP=2<5,
∴点P在⊙A内部.
故选:C.
2.(2021 兴化市模拟)若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. B.3π C.6π D.9π
【解析】解:S扇形==9π,
故选:D.
3.(2021 阜新)如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
【解析】解:∵∠AOB和∠C都对,
∴∠C=∠AOB=×70°=35°.
故选:B.
4.(2020秋 巩义市期末)如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50° B.75° C.65° D.60°
【解析】解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
5.(2021秋 江阴市期中)有下列说法:①任意三点确定一个圆;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
【解析】解:①不在同一直线上的三点确定一个圆,本说法错误;
②任意一个三角形有且仅有一个外接圆,本说法正确;
③长度相等的两条弧不一定是等弧,本说法错误;
④直径是圆中最长的弦,本说法正确;
故选:D.
6.(2021 拱墅区二模)如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m B.m C.5m D.m
【解析】解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=2(m),
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+22=OB2,
解得:OB=(m),
即这个轮子的半径长为m,
故选:D.
7.(2021 越秀区校级四模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=56°,则∠AOC的度数为( )
A.56° B.124° C.112° D.146°
【解析】解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,∠CBE=56°,
∴∠ADC=∠CBE=56°,
由圆周角定理得:∠AOC=2∠ADC=112°,
故选:C.
8.(2021 眉山)如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
【解析】解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵=3,
∴∠CAB=3∠ABC,
∴∠ABC=22.5°,∠CAB=67.5°,
∵CD⊥AB,
∴∠ACE=22.5°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=22.5°,
∵∠CAF=∠CBF,
∴∠CBF=22.5°,
故选:C.
9.(2021 安徽模拟)如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
【解析】解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
10.(2020春 海淀区校级月考)如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
【解析】解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r sin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
二.填空题
11.(2021 徐州)如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= 32 °.
【解析】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=∠ADC=58°,
∴∠BAC=90°﹣∠B=32°.
故答案为32.
12.(2021秋 海珠区校级期中)如图,E是正方形ABCD的边BC上一点,△ABE逆时针旋转后能够与△ADF重合,旋转中心是 点A ,旋转角为 90 度.
【解析】解:从图形和已知可知:旋转中心是点A,旋转角的度数等于∠BAD的度数,即为90°,
故答案为:点A;90.
13.(2021 济宁一模)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为 4 .
【解析】解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC==4,
故答案为:4.
14.(2020 娄底)如图,公路弯道标志表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B,则线段AB= 300 米.
【解析】解:设线段AB对应的圆心角度数为n,
∵100π==,
∴n=60°,
又AO=BO,
∴△AOB是等边三角形,
∴AB=AO=BO=300(米),
故答案为:300.
15.(2021 惠阳区二模)如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,若AD=3,则的长为 .
【解析】解:连接AC,AF,
∵四边形ABCD是正方形,
∴∠DAC=45°,AD=DC=3,∠ADC=90°,
由勾股定理得:AC===3,
∵将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线上,
∴A、D、F三点共线,A、E、C三点共线,
∴∠FAC=45°,
∴的长是=,
故答案为:.
16.如图,点C是扇形OAB上的的任意一点,∠AOB=90°,OA=2,连接AC,BC,过点O作OE⊥AC,OF⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
【解析】解:连接AB,如图,
∵OE⊥AC,OF⊥BC,
∴AE=CE,BF=CF,
∴EF为△CAB的中位线,
∴EF=AB,
∵∠AOB=90°,OA=OB,
∴AB=OA=2,
∴EF=.
故答案为.
三.解答题
17.(2021秋 香洲区校级期中)在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),若将△ABC绕点O逆时针旋转90°.
(1)画出旋转后的△A1B1C1;
(2)点A坐标为 (﹣4,4) ,B1坐标为 (﹣1,1) ,C1坐标为 (﹣1,3) .
【解析】解:(1)如图△A1B1C1即为所求;
(2)点A1坐标为(﹣4,4),B1坐标为(﹣1,1),C1坐标为(﹣1,3).
故答案为:(﹣4,4),(﹣1,1),(﹣1,3).
18.(2021 商河县校级模拟)一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
【解析】解:作半径OD⊥AB交AB于C,连接OB,如图所示,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下,水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
19.(2021 徐州)如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
【解析】证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
20.(2021春 永嘉县校级期末)如图,⊙O是△ABD的外接圆,AB为直径,点C是弧AD的中点,连接OC,BC分别交AD于点F,E.
(1)求证:∠ABD=2∠C.
(2)若AB=10,BC=8,求BD的长.
【解析】(1)证明:∵C是的中点,
∴=,
∴∠ABC=∠CBD,点F是AD的中点,
∵OB=OC,
∴∠ABC=∠C,
∴∠ABC=∠CBD=∠C,
∴∠ABD=∠ABC+CBD=2∠C;
(2)解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC==6,
∵C是的中点,
∴OC⊥AD,
∴OA2﹣OF2=AF2=AC2﹣CF2,
∴52﹣OF2=62﹣(5﹣OF)2,
∴OF=1.4,
又∵O是AB的中点,F是AD的中点,
∴OF是△ABD的中位线,
∴BD=2OF=2.8.
21.(2020秋 拱墅区校级期中)如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
【解析】解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
22.(2020秋 红谷滩区校级期末)如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8,求:
①⊙O的半径;
②求图中阴影部分的面积.
【解析】(1)证明:∵AB 为⊙O 的直径,AB⊥CD,
∴BC=BD,
∴∠A=∠DCB,
∴OF⊥AC,
∴∠AFO=∠CEB,
∵BE=OF,
∴△AFO≌△CEB(AAS).
(2)①∵AB 为⊙O 的直径,AB⊥CD,
∴CE=CD=4
设 OC=r,则 OE=r﹣4,
∴r2=(r﹣4)2+(4)2
∴r=8.
②连接 OD.
∵OE=4=OC,
∴∠OCE=30°,∠COB=60°,
∴∠COD=120°,
∵△AFO≌△CEB,
∴S△AFO=S△BCE,
∴S阴=S扇形OCD﹣S△OCD
=﹣××4
=π﹣16
23.已知:⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
(1)如图1,若AC⊥BD,点O到AD的距离为a,求证:BC=2a;
(2)如图2,若=,AD是⊙O的直径,AD=25,CD=7,求四边形ABCD的面积.
【解析】(1)证明:如图1中,作直径AF,连接DF,过点O作OG⊥AD于G.
∵AF是直径,
∴∠ADF=90°,
∴∠DAF+∠F=90°,
∵BD⊥AC,
∴∠CAB+∠ABD=90°,
∵∠ABD=∠F,
∴∠FAD=∠CAB,
∴=,
∴BC=DF,
∵OG⊥AD,
∴AG=DG,
∵AO=OF,
∴DF=2OG=2a,
∴BC=2a.
(2)解:如图2中,连接OB交AC于点Q.
∵=,
∴OB⊥AC,
∴AQ=CQ,
∵AO=OD,
∴OQ=CD=,
∵AD是直径,
∴∠ACD=90°,
∴AD===25,
∴OB=AD=,
∴BQ=OB﹣OQ=9,
∴S四边形ABCD=S△ACD+S△ABC=×AC×CD+×AC×BQ=×7×24+×24×9=192.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
