2021-2022学年浙教版九年级上第4章 相似三角形单元测试(1)(含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级上第4章 相似三角形单元测试(1)(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级上第4章 相似三角形单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2021 安徽模拟)如果,那么的值等于( )
A. B. C. D.2
2.(2021 醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
3.(2021春 泰山区期末)下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
4.(2019秋 滨湖区期末)若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
5.(2021 湘西州)如图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )
A.14 B.12.4 C.10.5 D.9.3
6.(2021春 芝罘区期末)如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
7.(2020秋 松北区期末)如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
8.(2018秋 仁寿县校级期中)如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④EF2=CF AF,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
9.(2021 蚌埠二模)如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为( )
A.5 B.6 C.9 D.
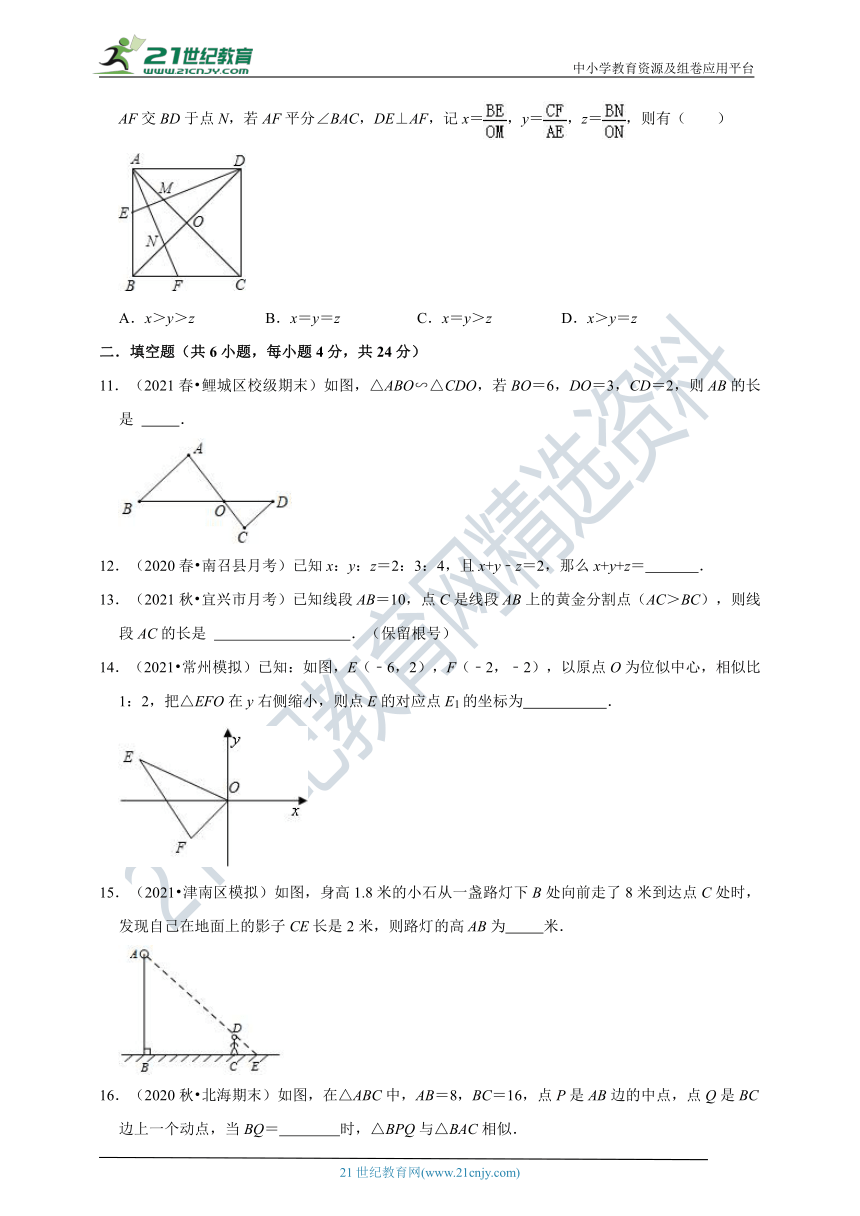
10.(2020 拱墅区四模)如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于点N,若AF平分∠BAC,DE⊥AF,记x=,y=,z=,则有( )
A.x>y>z B.x=y=z C.x=y>z D.x>y=z
二.填空题(共6小题,每小题4分,共24分)
11.(2021春 鲤城区校级期末)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是 .
12.(2020春 南召县月考)已知x:y:z=2:3:4,且x+y﹣z=2,那么x+y+z= .
13.(2021秋 宜兴市月考)已知线段AB=10,点C是线段AB上的黄金分割点(AC>BC),则线段AC的长是 .(保留根号)
14.(2021 常州模拟)已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 .
15.(2021 津南区模拟)如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
16.(2020秋 北海期末)如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
三.解答题(共7小题,共66分)
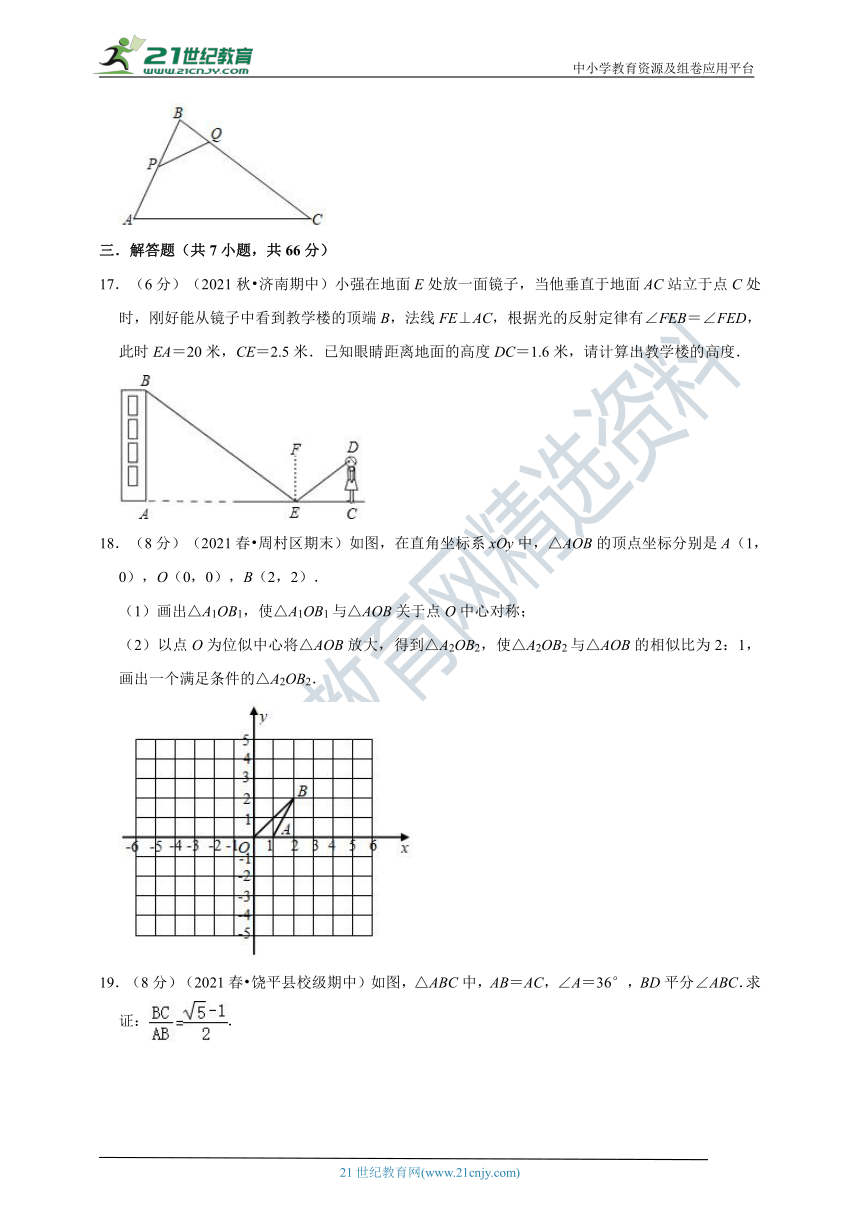
17.(6分)(2021秋 济南期中)小强在地面E处放一面镜子,当他垂直于地面AC站立于点C处时,刚好能从镜子中看到教学楼的顶端B,法线FE⊥AC,根据光的反射定律有∠FEB=∠FED,此时EA=20米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.
18.(8分)(2021春 周村区期末)如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
19.(8分)(2021春 饶平县校级期中)如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC.求证:.
20.(10分)(2021秋 灯塔市校级期中)如图,四边形ABCD的对角线AC,BD交于点E,点F是AC上一点,且∠ADB=∠FDC=∠ACB.
(1)求证:△ADF∽△BDC;
(2)若AB=4,CD=9,CF=6,求BD的长.
21.(10分)(2020秋 沈北新区期末)如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
22.(12分)(2020秋 庐阳区校级期末)如图,AB为⊙O的直径,C为⊙O上一点,连接AC、BC、OC,过点B作BG⊥OC交OC于点E,交AC于点F,交⊙O于点G.
(1)求证:∠CAB=∠CBG;
(2)求证:BC2=AB CE.
23.(12分)(2021春 泰山区期末)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
答案与解析
一.选择题
1.(2021 安徽模拟)如果,那么的值等于( )
A. B. C. D.2
【解析】解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
2.(2021 醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
【解析】解:∵直线l1∥l2∥l3,
∴=,
∵AB=2,BC=3,EF=2,
∴=,
∴DE=,
故选:B.
3.(2021春 泰山区期末)下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
【解析】解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
4.(2019秋 滨湖区期末)若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
【解析】解:∵两个相似多边形的面积之比为4:9,
∴两个相似多边形的对应边的比为2:3,
∴两个相似多边形的周长的比为2:3,
故选:B.
5.(2021 湘西州)如图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )
A.14 B.12.4 C.10.5 D.9.3
【解析】解:∵EB=1.6,BC=12.4,
∴EC=EB+BC=14,
∵AB⊥EC,
∴∠ABE=90°,
∵∠C=90°,
∴∠ABE=∠C,
又∵∠E=∠E,
∴△ABE∽△DCE,
∴=,
即=,
解得:CD=10.5,
故选:C.
6.(2021春 芝罘区期末)如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
【解析】解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
7.(2020秋 松北区期末)如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴△EAG∽△EBF,△EAG∽△HDG,
∴,,故选项A、B成立,
∵CH∥BA,
∴,
∴,故选项C正确,
∵AG∥AC,CH∥BA,
∴,,
而无法证明是否成立,故选项D不一定成立,
故选:D.
8.(2018秋 仁寿县校级期中)如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④EF2=CF AF,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠D=90°
∵E是BC的中点,
∴BE=CE=BC=AB,
在Rt△ABE中,tan∠BAE==<,
∵tan30°=,
∴∠BAE<30°,
所以①错误;
∴=2
∵CD=4CF,
∴=2,
∴=,
∵∠B=∠C,
∴△ABE∽△ECF,
∴∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°,
∴AE⊥EF,
所以③正确;
∵=2,==2,
∴=,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
所以②正确,
∵△ABE∽△AEF,△ABE∽△ECF,
∴△AEF∽△ECF,
∴=,
∴EF2=CF AF,
所以④正确;
故选:C.
9.(2021 蚌埠二模)如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为( )
A.5 B.6 C.9 D.
【解析】解:∵S△ADC:S△BDC=5:4,
∴S△BCD:S△ABC=4:9,
∵∠A=∠BCD,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴=()2=,
∴=,
∴AC=6,
故选:B.
10.(2020 拱墅区四模)如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于点N,若AF平分∠BAC,DE⊥AF,记x=,y=,z=,则有( )
A.x>y>z B.x=y=z C.x=y>z D.x>y=z
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=90°,∠BAC=45°,
∴∠BAF+∠AFB=90°,
∵DE⊥AF,
∴∠BAF+∠DEA=90°,
∴∠AFB=∠DEA,
在△AFB和△DEA,
,
∴△AFB≌△DEA(AAS),
∴∠BAF=∠ADE,BF=AE,
∵AF平分∠BAC,
∴∠BAF=∠CAF=22.5°,
∴∠ADE=∠BDE=22.5°,
∵∠ABF=∠AON=90°,∠BAF=∠NAO,
∴△ABF∽△AON,
∵∠BAN=∠CAF,∠ABN=∠ACF=45°,
∴△BAN∽△CAF,
∴y=
=
=
=,
z=
=
=,
∴y=z,
∵BF=AE,AB=BC,
∴BE=CF,
∴==,
∵∠ADE=22.5°,∠EAD=90°,
∴∠AEM=67.5°,∠AME=∠ADE+∠MAD=67.5°,
∴∠AEM=∠AME,
∴AE=AM,
过点M作MH⊥AD于点H,如图:
∵∠ADE=22.5°,∠EDB=45°,
∴∠MDO=∠MDH=22.5°,
∵MH⊥AD,MO⊥AC,
∴OM=HM,
∵∠MAH=45°,∠MHA=90°,
∴AM=HM=OM,
∴AE=OM,
∴BE=AE=2OM,
∴x==2,
∴x>y=z.
二.填空题
11.(2021春 鲤城区校级期末)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是 4 .
【解析】解:∵△ABO∽△CDO,
∴=,
∵BO=6,DO=3,CD=2,
∴=,
解得:AB=4.
故答案为:4.
12.(2020春 南召县月考)已知x:y:z=2:3:4,且x+y﹣z=2,那么x+y+z= 18 .
【解析】解:∵x:y:z=2:3:4,
∴设x=2a,y=3a,z=4a,
故x+y﹣z=2a+3a﹣4a=a=2,
故x=4,y=6,z=8,
∴x+y+z=4+6+8=18.
故答案为:18.
13.(2021秋 宜兴市月考)已知线段AB=10,点C是线段AB上的黄金分割点(AC>BC),则线段AC的长是 .(保留根号)
【解析】解:∵点C是线段AB上的黄金分割点(AC>BC),
∴AC=AB=×10=5﹣5,
∴AC=5﹣5,
故答案为:5﹣5.
14.(2021 常州模拟)已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 (3,﹣1) .
【解析】解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
15.(2021 津南区模拟)如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 9 米.
【解析】解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
16.(2020秋 北海期末)如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 2或8 时,△BPQ与△BAC相似.
【解析】解:∵AB=8,BC=16,点P是AB边的中点,
∴BP=4.
当△BPQ∽△BAC时,
则=,
故=,
解得:BQ=8;
当△BPQ∽△BCA时,
则=,
故=,
解得:BQ=2,
综上所述:当BQ=2或8时,△BPQ与△BAC相似.
故答案为:2或8.
三.解答题
17.(2021秋 济南期中)小强在地面E处放一面镜子,当他垂直于地面AC站立于点C处时,刚好能从镜子中看到教学楼的顶端B,法线FE⊥AC,根据光的反射定律有∠FEB=∠FED,此时EA=20米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.
【解析】解:根据题意得∠AEB=∠CED,∠BAE=∠DCE=90°,
∴△AEB∽△CED,
∴=,
即=,
解得:AB=12.8(米).
答:教学楼AB的高度为12.8米.
18.(2021春 周村区期末)如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
【解析】解:(1)如图所示,△A1OB1即为所求;
(2)如图所示,△A2OB2即为所求.
19.(2021春 饶平县校级期中)如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC.求证:.
【解析】解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC,
∵∠A=∠CBD,∠C=∠C,
∴△ABC∽△BDC,
∴BC:DC=AC:BC,
∴AD:DC=AC:AD,
∴点D为AC的黄金分割点,
∴=,
∴.
20.(2021秋 灯塔市校级期中)如图,四边形ABCD的对角线AC,BD交于点E,点F是AC上一点,且∠ADB=∠FDC=∠ACB.
(1)求证:△ADF∽△BDC;
(2)若AB=4,CD=9,CF=6,求BD的长.
【解析】(1)证明:∵∠ADB=∠FDC=∠ACB,
∴∠ADB+∠BDF=∠FDC+∠BDF,∠FDC+∠DCF=∠ACB+∠DCF,
∴∠ADF=∠CDB,∠AFD=∠DCB,
∴△ADF∽△BDC;
(2)解:∵△ADF∽△BDC,
∴,
又∵∠ADB=∠FDC,
∴△ADB∽△FDC,
∴,
∵AB=4,CD=9,CF=6,
∴,
∴BD=6.
21.(2020秋 沈北新区期末)如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
【解析】证明:(1)∵AD∥BC,
∴∠ADM=∠NBM,∠DAM=∠BNM,
∴△ADM∽△NBM,
∴=,
∵AB∥DC,
∴∠P=∠BAM,∠MDP=∠ABM,
∴△PDM∽△ABM,
∴=,
∴=,
∴AM2=MN MP;
(2)∵AD∥BC,
∴∠PCN=∠PDA,∠P=∠P,
∴△PCN∽△PDA,
∴=,
∵DC:CP=2:1,
∴==,
又∵AD=6,
∴NC=2,
∴BN=4.
22.(2020秋 庐阳区校级期末)如图,AB为⊙O的直径,C为⊙O上一点,连接AC、BC、OC,过点B作BG⊥OC交OC于点E,交AC于点F,交⊙O于点G.
(1)求证:∠CAB=∠CBG;
(2)求证:BC2=AB CE.
【解析】(1)证明:如图,连接CG,
∵OC⊥BG,
∴C为BG中点,,
∴∠CGB=∠CBG,
∵所対圆周角为∠CAB和∠CGB,
∴∠CAB=∠CGB,
∴∠CAB=∠CBG;
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB=∠CEB=90°,
∴∠CAB=∠CBE,
∴△CEB∽△BCA,
∴,
∴BC2=AB CE.
23.(2021春 泰山区期末)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
【解析】解:(1)∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,
∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=3;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴AC=DC,
∵∠B=45°,
∴∠C=45°,∠BAC=90°,
∵BC=6,
∴,
∴,
综上所述,当△ADE是等腰三角形时,BD的长为3或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级上第4章 相似三角形单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2021 安徽模拟)如果,那么的值等于( )
A. B. C. D.2
2.(2021 醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
3.(2021春 泰山区期末)下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
4.(2019秋 滨湖区期末)若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
5.(2021 湘西州)如图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )
A.14 B.12.4 C.10.5 D.9.3
6.(2021春 芝罘区期末)如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
7.(2020秋 松北区期末)如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
8.(2018秋 仁寿县校级期中)如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④EF2=CF AF,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
9.(2021 蚌埠二模)如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为( )
A.5 B.6 C.9 D.
10.(2020 拱墅区四模)如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于点N,若AF平分∠BAC,DE⊥AF,记x=,y=,z=,则有( )
A.x>y>z B.x=y=z C.x=y>z D.x>y=z
二.填空题(共6小题,每小题4分,共24分)
11.(2021春 鲤城区校级期末)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是 .
12.(2020春 南召县月考)已知x:y:z=2:3:4,且x+y﹣z=2,那么x+y+z= .
13.(2021秋 宜兴市月考)已知线段AB=10,点C是线段AB上的黄金分割点(AC>BC),则线段AC的长是 .(保留根号)
14.(2021 常州模拟)已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 .
15.(2021 津南区模拟)如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
16.(2020秋 北海期末)如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
三.解答题(共7小题,共66分)
17.(6分)(2021秋 济南期中)小强在地面E处放一面镜子,当他垂直于地面AC站立于点C处时,刚好能从镜子中看到教学楼的顶端B,法线FE⊥AC,根据光的反射定律有∠FEB=∠FED,此时EA=20米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.
18.(8分)(2021春 周村区期末)如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
19.(8分)(2021春 饶平县校级期中)如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC.求证:.
20.(10分)(2021秋 灯塔市校级期中)如图,四边形ABCD的对角线AC,BD交于点E,点F是AC上一点,且∠ADB=∠FDC=∠ACB.
(1)求证:△ADF∽△BDC;
(2)若AB=4,CD=9,CF=6,求BD的长.
21.(10分)(2020秋 沈北新区期末)如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
22.(12分)(2020秋 庐阳区校级期末)如图,AB为⊙O的直径,C为⊙O上一点,连接AC、BC、OC,过点B作BG⊥OC交OC于点E,交AC于点F,交⊙O于点G.
(1)求证:∠CAB=∠CBG;
(2)求证:BC2=AB CE.
23.(12分)(2021春 泰山区期末)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
答案与解析
一.选择题
1.(2021 安徽模拟)如果,那么的值等于( )
A. B. C. D.2
【解析】解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
2.(2021 醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
【解析】解:∵直线l1∥l2∥l3,
∴=,
∵AB=2,BC=3,EF=2,
∴=,
∴DE=,
故选:B.
3.(2021春 泰山区期末)下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
【解析】解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
4.(2019秋 滨湖区期末)若两个相似多边形的面积之比为4:9,则这两个多边形的周长之比为( )
A.: B.2:3 C.4:9 D.16:81
【解析】解:∵两个相似多边形的面积之比为4:9,
∴两个相似多边形的对应边的比为2:3,
∴两个相似多边形的周长的比为2:3,
故选:B.
5.(2021 湘西州)如图,在△ECD中,∠C=90°,AB⊥EC于点B,AB=1.2,EB=1.6,BC=12.4,则CD的长是( )
A.14 B.12.4 C.10.5 D.9.3
【解析】解:∵EB=1.6,BC=12.4,
∴EC=EB+BC=14,
∵AB⊥EC,
∴∠ABE=90°,
∵∠C=90°,
∴∠ABE=∠C,
又∵∠E=∠E,
∴△ABE∽△DCE,
∴=,
即=,
解得:CD=10.5,
故选:C.
6.(2021春 芝罘区期末)如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
【解析】解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
7.(2020秋 松北区期末)如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴△EAG∽△EBF,△EAG∽△HDG,
∴,,故选项A、B成立,
∵CH∥BA,
∴,
∴,故选项C正确,
∵AG∥AC,CH∥BA,
∴,,
而无法证明是否成立,故选项D不一定成立,
故选:D.
8.(2018秋 仁寿县校级期中)如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④EF2=CF AF,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠D=90°
∵E是BC的中点,
∴BE=CE=BC=AB,
在Rt△ABE中,tan∠BAE==<,
∵tan30°=,
∴∠BAE<30°,
所以①错误;
∴=2
∵CD=4CF,
∴=2,
∴=,
∵∠B=∠C,
∴△ABE∽△ECF,
∴∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°,
∴AE⊥EF,
所以③正确;
∵=2,==2,
∴=,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
所以②正确,
∵△ABE∽△AEF,△ABE∽△ECF,
∴△AEF∽△ECF,
∴=,
∴EF2=CF AF,
所以④正确;
故选:C.
9.(2021 蚌埠二模)如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为( )
A.5 B.6 C.9 D.
【解析】解:∵S△ADC:S△BDC=5:4,
∴S△BCD:S△ABC=4:9,
∵∠A=∠BCD,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴=()2=,
∴=,
∴AC=6,
故选:B.
10.(2020 拱墅区四模)如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于点N,若AF平分∠BAC,DE⊥AF,记x=,y=,z=,则有( )
A.x>y>z B.x=y=z C.x=y>z D.x>y=z
【解析】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=90°,∠BAC=45°,
∴∠BAF+∠AFB=90°,
∵DE⊥AF,
∴∠BAF+∠DEA=90°,
∴∠AFB=∠DEA,
在△AFB和△DEA,
,
∴△AFB≌△DEA(AAS),
∴∠BAF=∠ADE,BF=AE,
∵AF平分∠BAC,
∴∠BAF=∠CAF=22.5°,
∴∠ADE=∠BDE=22.5°,
∵∠ABF=∠AON=90°,∠BAF=∠NAO,
∴△ABF∽△AON,
∵∠BAN=∠CAF,∠ABN=∠ACF=45°,
∴△BAN∽△CAF,
∴y=
=
=
=,
z=
=
=,
∴y=z,
∵BF=AE,AB=BC,
∴BE=CF,
∴==,
∵∠ADE=22.5°,∠EAD=90°,
∴∠AEM=67.5°,∠AME=∠ADE+∠MAD=67.5°,
∴∠AEM=∠AME,
∴AE=AM,
过点M作MH⊥AD于点H,如图:
∵∠ADE=22.5°,∠EDB=45°,
∴∠MDO=∠MDH=22.5°,
∵MH⊥AD,MO⊥AC,
∴OM=HM,
∵∠MAH=45°,∠MHA=90°,
∴AM=HM=OM,
∴AE=OM,
∴BE=AE=2OM,
∴x==2,
∴x>y=z.
二.填空题
11.(2021春 鲤城区校级期末)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是 4 .
【解析】解:∵△ABO∽△CDO,
∴=,
∵BO=6,DO=3,CD=2,
∴=,
解得:AB=4.
故答案为:4.
12.(2020春 南召县月考)已知x:y:z=2:3:4,且x+y﹣z=2,那么x+y+z= 18 .
【解析】解:∵x:y:z=2:3:4,
∴设x=2a,y=3a,z=4a,
故x+y﹣z=2a+3a﹣4a=a=2,
故x=4,y=6,z=8,
∴x+y+z=4+6+8=18.
故答案为:18.
13.(2021秋 宜兴市月考)已知线段AB=10,点C是线段AB上的黄金分割点(AC>BC),则线段AC的长是 .(保留根号)
【解析】解:∵点C是线段AB上的黄金分割点(AC>BC),
∴AC=AB=×10=5﹣5,
∴AC=5﹣5,
故答案为:5﹣5.
14.(2021 常州模拟)已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 (3,﹣1) .
【解析】解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
15.(2021 津南区模拟)如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 9 米.
【解析】解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
16.(2020秋 北海期末)如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 2或8 时,△BPQ与△BAC相似.
【解析】解:∵AB=8,BC=16,点P是AB边的中点,
∴BP=4.
当△BPQ∽△BAC时,
则=,
故=,
解得:BQ=8;
当△BPQ∽△BCA时,
则=,
故=,
解得:BQ=2,
综上所述:当BQ=2或8时,△BPQ与△BAC相似.
故答案为:2或8.
三.解答题
17.(2021秋 济南期中)小强在地面E处放一面镜子,当他垂直于地面AC站立于点C处时,刚好能从镜子中看到教学楼的顶端B,法线FE⊥AC,根据光的反射定律有∠FEB=∠FED,此时EA=20米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.
【解析】解:根据题意得∠AEB=∠CED,∠BAE=∠DCE=90°,
∴△AEB∽△CED,
∴=,
即=,
解得:AB=12.8(米).
答:教学楼AB的高度为12.8米.
18.(2021春 周村区期末)如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
【解析】解:(1)如图所示,△A1OB1即为所求;
(2)如图所示,△A2OB2即为所求.
19.(2021春 饶平县校级期中)如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC.求证:.
【解析】解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC,
∵∠A=∠CBD,∠C=∠C,
∴△ABC∽△BDC,
∴BC:DC=AC:BC,
∴AD:DC=AC:AD,
∴点D为AC的黄金分割点,
∴=,
∴.
20.(2021秋 灯塔市校级期中)如图,四边形ABCD的对角线AC,BD交于点E,点F是AC上一点,且∠ADB=∠FDC=∠ACB.
(1)求证:△ADF∽△BDC;
(2)若AB=4,CD=9,CF=6,求BD的长.
【解析】(1)证明:∵∠ADB=∠FDC=∠ACB,
∴∠ADB+∠BDF=∠FDC+∠BDF,∠FDC+∠DCF=∠ACB+∠DCF,
∴∠ADF=∠CDB,∠AFD=∠DCB,
∴△ADF∽△BDC;
(2)解:∵△ADF∽△BDC,
∴,
又∵∠ADB=∠FDC,
∴△ADB∽△FDC,
∴,
∵AB=4,CD=9,CF=6,
∴,
∴BD=6.
21.(2020秋 沈北新区期末)如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
【解析】证明:(1)∵AD∥BC,
∴∠ADM=∠NBM,∠DAM=∠BNM,
∴△ADM∽△NBM,
∴=,
∵AB∥DC,
∴∠P=∠BAM,∠MDP=∠ABM,
∴△PDM∽△ABM,
∴=,
∴=,
∴AM2=MN MP;
(2)∵AD∥BC,
∴∠PCN=∠PDA,∠P=∠P,
∴△PCN∽△PDA,
∴=,
∵DC:CP=2:1,
∴==,
又∵AD=6,
∴NC=2,
∴BN=4.
22.(2020秋 庐阳区校级期末)如图,AB为⊙O的直径,C为⊙O上一点,连接AC、BC、OC,过点B作BG⊥OC交OC于点E,交AC于点F,交⊙O于点G.
(1)求证:∠CAB=∠CBG;
(2)求证:BC2=AB CE.
【解析】(1)证明:如图,连接CG,
∵OC⊥BG,
∴C为BG中点,,
∴∠CGB=∠CBG,
∵所対圆周角为∠CAB和∠CGB,
∴∠CAB=∠CGB,
∴∠CAB=∠CBG;
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB=∠CEB=90°,
∴∠CAB=∠CBE,
∴△CEB∽△BCA,
∴,
∴BC2=AB CE.
23.(2021春 泰山区期末)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
【解析】解:(1)∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,
∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=3;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴AC=DC,
∵∠B=45°,
∴∠C=45°,∠BAC=90°,
∵BC=6,
∴,
∴,
综上所述,当△ADE是等腰三角形时,BD的长为3或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
