相似三角形复习

(共17张PPT)
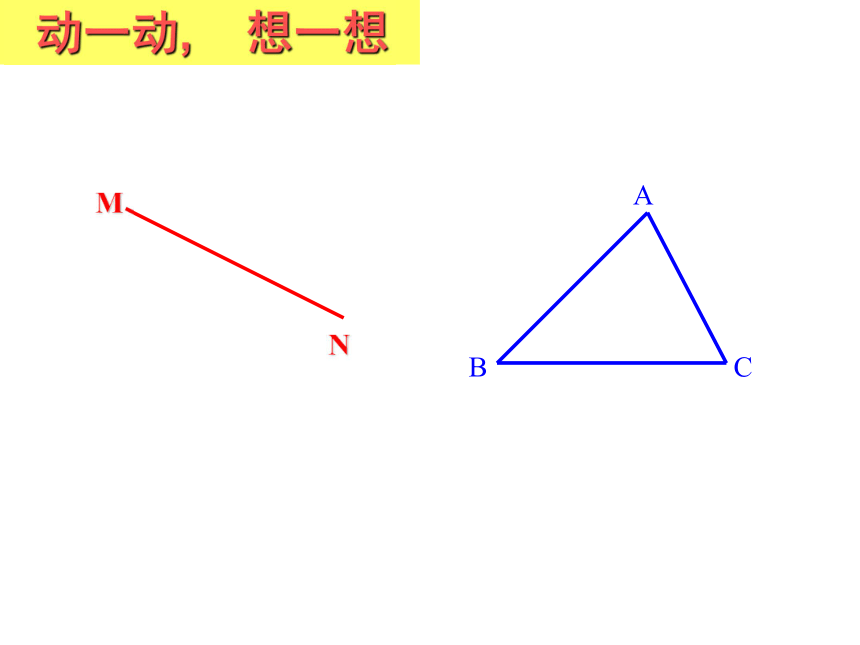
动一动, 想一想
A
B
C
M
N
相似三角形的判定方法
1、平行于三角形一边的直线和其他两边相交，所构 成的三角形与原三角形相似
2、有两角对应相等的两个三角形相似
3、两边对应成比例,且夹角相等的两个三角形相似
4、三边对应成比例的两个三角形相似
梳理一
A
C
B
E
D
4
3
2
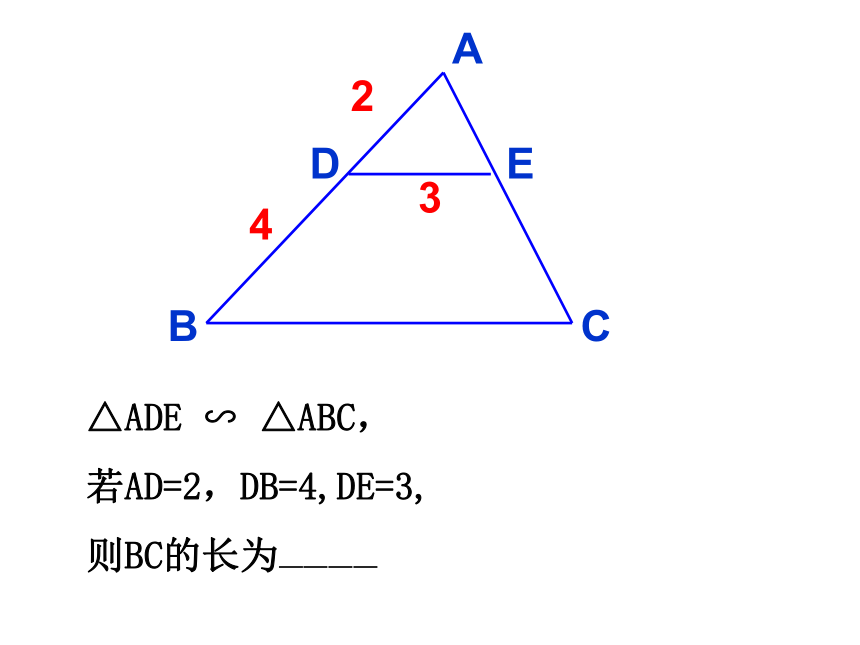
△ADE ∽ △ABC，
若AD=2，DB=4,DE=3,
则BC的长为————
A
C
B
E
D
3
1
3
1
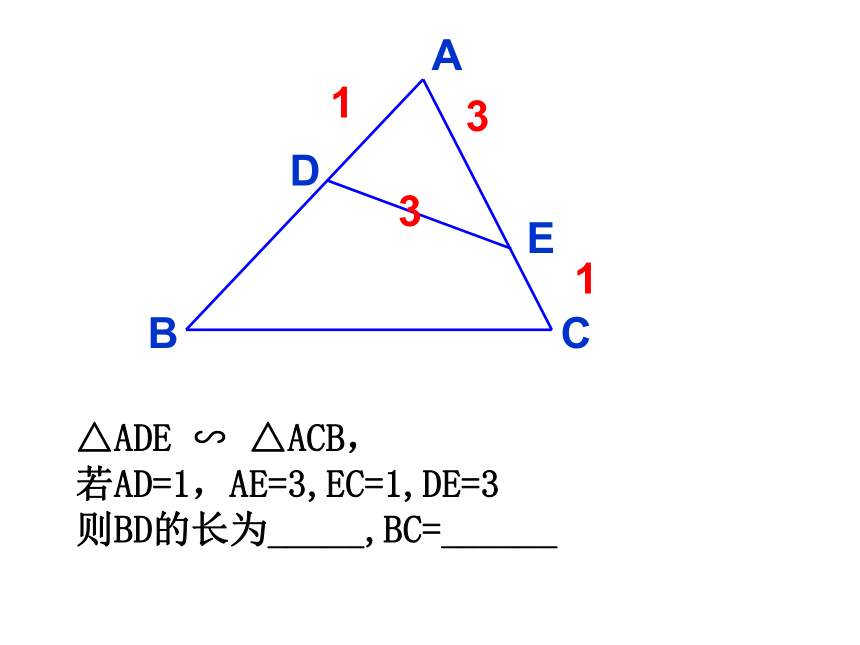
△ADE ∽ △ACB，
若AD=1，AE=3,EC=1,DE=3
则BD的长为_____,BC=______
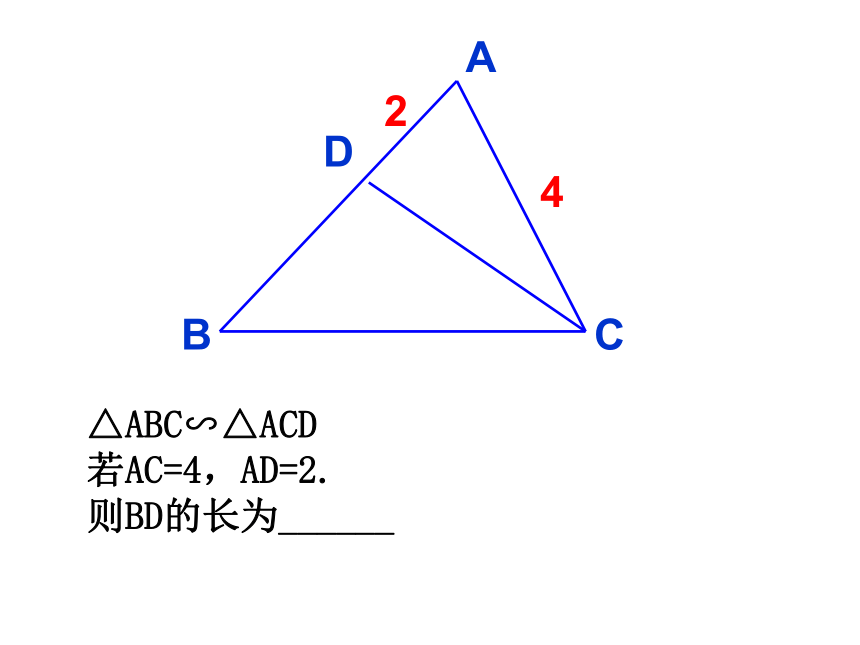
△ABC∽△ACD
若AC=4，AD=2.
则BD的长为______
A
C
B
D
2
4
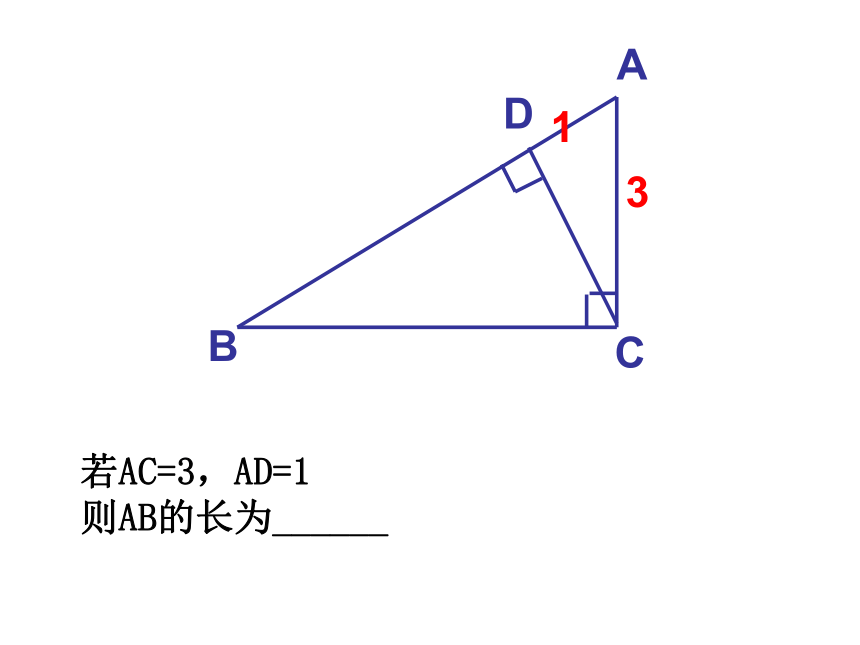
若AC=3，AD=1
则AB的长为______
A
C
B
D
1
3
B
F
A
C
E
D
4
3
2
G
△ADE ∽△ABC
若AD=2，BD=4,AG=3.
则AF的长为______, FG的长为______
(1) AG：AF=————；
（2）△ADE与△ABC的周长之比；
（3）△ADE与△ABC的面积之比．
△ABC∽△AED
AE=3，AB=5
相似三角形的性质
2、相似三角形的周长之比等于相似比
3、相 似三角形的面积之比等于相似比的平方
4、相 似三角形对应边上的高之比等于相似比
梳理二
1、相似三角形的对应角相等，对应边成 比例
△ADE绕点A
旋转
A
C
B
D
A
D
E
B
C
A
D
E
B
C
A
B
C
D
E
B
C
A
D
E
点E移到与C点
重合
∠ACB=Rt∠
CD⊥AB
相似三角形基本图形的回顾：
A
B
C
D
直角梯形ABCD,∠A=∠B=90°，AD=2，BC=8，AB=10，要使∠DPC =90°,
求PA
有一块三角形铁皮，为了更好地利用它，请你剪出一个面积最大的矩形，使矩形的其中一边在三角形一边上，应如何剪呢？
用一用
A
B
C
D
8
6
已知二次函数的图象经过A（1，0）、B（3，0），C（0,3），设顶点为点P，对称轴与x轴交于点D
（2）点M、N分别在OP和PB上，MN∥x轴，若△PMN沿MN折叠，使△PMN落在四边形 OMNB所在平面上，设点P落在平面上的点为P’，△PMN与梯形OMNB的重叠部分的面积为S，设MN 为x．求S关于x的函数关系式．
（1）在对称轴上找一点E，使△AOC与△EAD相似,求点E的坐标
我知道了…………
　我感到困难的是…………
课堂小结
本堂课体现了哪些数学思想方法：
数形结合的思想方法
分类讨论的思想方法
类比的思想方法
本堂课体现了哪些知识点：
方程的思想方法
相似三角形的性质和判定
笛卡尔说过:我所解决的每一个问题都将成为一个范例,以用于解决其他问题,这便是学习数学的真谛!