2021-2022学年浙教版八年级数学上册第4章图形与坐标 单元达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册第4章图形与坐标 单元达标测评(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学上册《第4章图形与坐标》单元达标测评(附答案)
一.选择题(共9小题,满分36分)
1.平面直角坐标系中第四象限有一点P,点P到y轴的距离为2,到x轴的距离为3,则点P的坐标是( )
A.(3,﹣2) B.(﹣2,3)
C.(2,﹣3) D.(2,﹣3)或(3,﹣2)
2.若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
3.在平面直角坐标系中,若点P(a,b)在第四象限,则点Q(1+a,1﹣b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→…根据这个规律,第2020个点的坐标为( )
A.(45,5) B.(45,6) C.(45,7) D.(45,8)
5.平面直角坐标系内有点A(﹣2,3),B(4,3),则A,B相距( )
A.4个单位长度 B.5个单位长度
C.6个单位长度 D.10个单位长度
6.如图,动点P从点(3,0)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(0,3)……第2018次碰到长方形边上的坐标为( )
A.(1,4) B.(5,0) C.(8,3) D.(7,4)
7.已知(a﹣2)2+|b+3|=0,则P(﹣a,﹣b)关于x轴对称点的坐标为( )
A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
8.在平面直角坐标系内,线段MN的两个端点坐标分别为M(﹣1,2)、N(2,1),平移线段MN得到线段M′N′,若M′的坐标为(0,1),则N′的坐标为( )
A.(3,2) B.(1,2) C.(1,0) D.(3,0)
9.若点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A.(4,﹣2) B.(3,﹣1)
C.(3,﹣1)或(3,﹣3) D.(4,﹣2)或(2,﹣2)
二.填空题(共6小题,满分30分)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
11.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)根据这个规律探索可得,第100个点的坐标为 .
12.若+(b+2)2=0,则点M(a,b)关于y轴的对称点的坐标为 .
13.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
14.已知线段AB∥x轴,AB=3,A点的坐标为(1,2),则点B的坐标为 .
15.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
三.解答题(共5小题,满分54分)
16.已知:P(4x,x﹣3)在平面直角坐标系中,
(1)若点P在第三象限的角平分线上,求x的值;
(2)若点P在第四象限,且到两坐标轴的距离之和为9,求x的值.
17.如图,在平面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求三角形ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
18.已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置;
(2)求出以A、B、C三点为顶点的三角形的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10,若存在,请直接写出点P的坐标;若不存在,请说明理由.
19.在平面直角坐标系中,A(a,b),B(2,2),且|a﹣b+8|+=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,求三角形ABC的面积;
(3)在(2)的条件下,延长AB交x轴于点D,AB交y轴于点E,那么OD与OE是否相等,请说明理由.
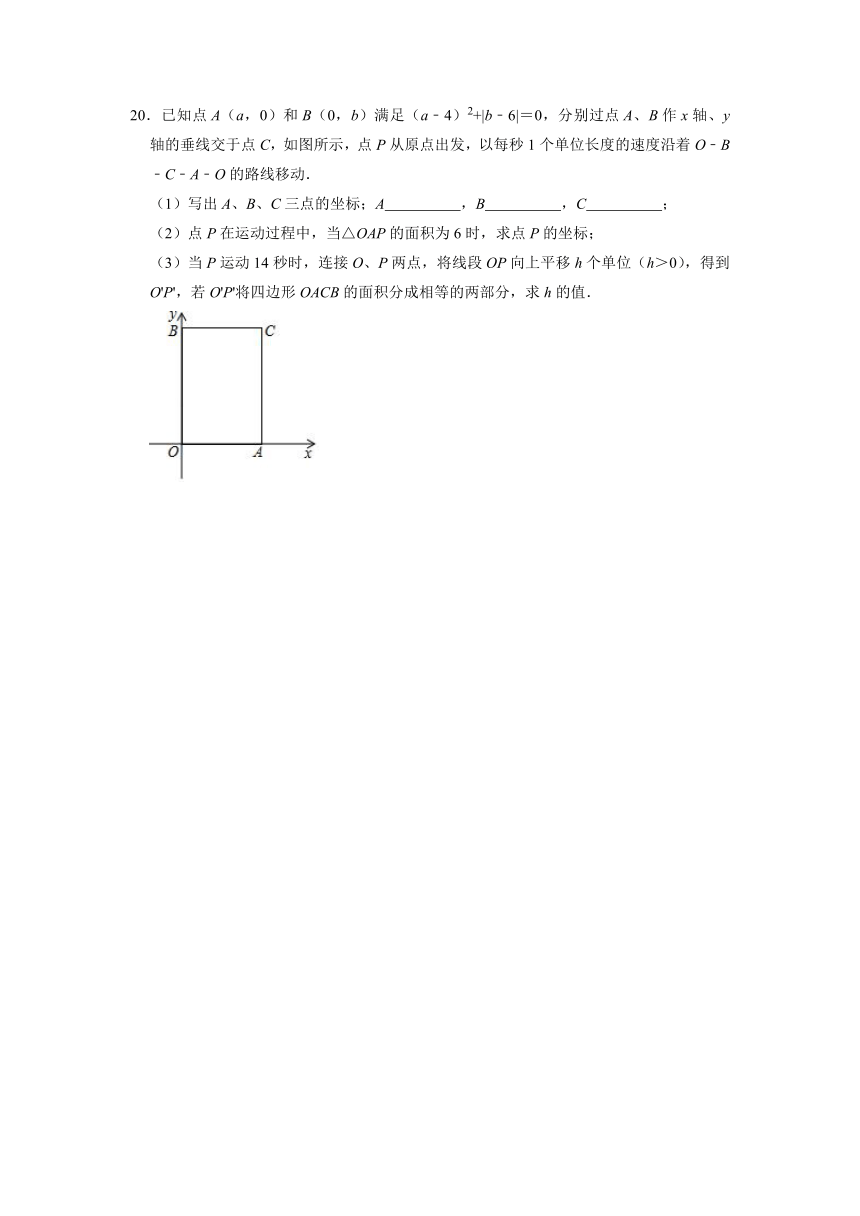
20.已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图所示,点P从原点出发,以每秒1个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动.
(1)写出A、B、C三点的坐标;A ,B ,C ;
(2)点P在运动过程中,当△OAP的面积为6时,求点P的坐标;
(3)当P运动14秒时,连接O、P两点,将线段OP向上平移h个单位(h>0),得到O'P',若O'P'将四边形OACB的面积分成相等的两部分,求h的值.
参考答案
一.选择题(共9小题,满分36分)
1.解:∵第四象限的点P到x轴的距离是3,到y轴的距离是2,
∴点P的横坐标是2,纵坐标是﹣3,
∴点P的坐标为(2,﹣3).故选:C.
2.解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得:a=2,故选:A.
3.解:∵点P(a,b)在第四象限,
∴a>0,b<0,
故1+a>0,1﹣b>0,
则点Q(1+a,1﹣b)在第一象限.故选:A.
4.解:由图形可知,图中各点分别组成了正方形点阵,每个正方形点阵的整点数量依次为最右下角点横坐标的平方
且当正方形最右下角点的横坐标为奇数时,这个点可以看做按照运动方向到达x轴,当正方形最右下角点的横坐标为偶数时,这个点可以看做按照运动方向离开x轴
∵452=2025
∴第2025个点在x轴上坐标为(45,0)
则第2020个点在(45,5)故选:A.
5.解:如图,A、B间的距离为6个单位长度.
故选:C.
6.解:根据题意,如下图示:
通过上图观察可知,每碰撞6次回到始点.
∵2018÷6=336…2,
∴第2018次碰到长方形边上的点的坐标与第二次相同,即坐标为(1,4).
故选:A.
7.解:∵(a﹣2)2+|b+3|=0,
∴a=2,b=﹣3,
根据平面直角坐标系中对称点的规律可知:
点P(﹣2,3)关于x轴对称的点的坐标为(﹣2,﹣3).
故选:D.
8.解:∵点M(﹣1,2)平移后的对应点M′的坐标为(0,1),
∴线段MN的平移方向和距离为:向右平移1个单位,向下平移1个单位,
则点N(2,1)平移后的对应点N′的坐标为(3,0),
故选:D.
9.解:∵点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,MN=1,
∴y=﹣2,|x﹣3|=1,
∴x=2或4,
∴N点的坐标为(2,﹣2)或(4,﹣2).
故选:D.
二.填空题(共6小题,满分30分)
10.解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
11.解:因为1+2+3+…+13=91,所以第91个点的坐标为(13,0).
因为在第14列点的走向为向上,故第100个点在此行上,横坐标就为14,纵坐标为从第92个点向上数8个点,即为8;
故第100个点的坐标为(14,8).
故填(14,8).
12.解:∵+(b+2)2=0,
∴a=3,b=﹣2;
∴点M(a,b)关于y轴的对称点的坐标为(﹣3,﹣2).
13.解:因为点D(5,3)在边AB上,
所以AB=BC=5,BD=5﹣3=2;
(1)若把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(﹣2,0);
(2)若把△CDB逆时针旋转90°,
则点D′到x轴的距离为10,到y轴的距离为2,
所以D′(2,10),
综上,旋转后点D的对应点D′的坐标为(﹣2,0)或(2,10).
故答案为:(﹣2,0)或(2,10).
14.解:∵线段AB∥x轴,AB=3,A点的坐标为(1,2),
设点B的坐标为(b,2),
∴|1﹣b|=3,
解得,b=﹣2或b=4,
∴点B的坐标为:(﹣2,2)或(4,2),
故答案为:(﹣2,2)或(4,2).
15.解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(﹣4,3).
故答案为:(﹣4,3).
三.解答题(共5小题,满分54分)
16.解:(1)由题意,得
4x=x﹣3,
解得x=﹣1
∴点P在第三象限的角平分线上时,x=﹣1.
(2)由题意,得
4x+[﹣(x﹣3)]=9,
则3x=6,
解得x=2,此时点P的坐标为(8,﹣1),
∴当点P在第四象限,且到两坐标轴的距离之和为9时,x=2.
17.解:(1)已知点A(0,2),B(3,0),C(3,4),
过A点作BC边上的高,交BC于点H,
则三角形ABC的面积为:S=BC AH=×4×3=6;
(2)四边形ABOP的面积可以看作是△APO和△AOB的面积和,
∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO=+×(﹣m)×2=3﹣m.
故四边形ABOP的面积为3﹣m;
(3)当四边形ABOP的面积与△ABC的面积相等时,
即3﹣m=6,得m=﹣3,
此时P点坐标为:(﹣3,),
存在P点,使四边形ABOP的面积与△ABC的面积相等.
18.解:(1)描点如图;
(2)依题意,得AB∥x轴,且AB=3﹣(﹣2)=5,
∴S△ABC=×5×2=5;
(3)存在;
∵AB=5,S△ABP=10,
∴P点到AB的距离为4,
又点P在y轴上,
∴P点的坐标为(0,5)或(0,﹣3).
19.解:(1)由|a﹣b+8|+=0,得
,
解得:.
∴点A的坐标为(﹣2,6);
(2)如图1,过B作BF⊥x轴于F,三角形ABC的面积=梯形ACFB的面积﹣三角形BCF的面积
=
=(2+6)×4
=12;
(3)如图2,OD与OE相等.
理由如下:
设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y,
因为,三角形ABC的面积=三角形ACD的面积﹣三角形BCD的面积,
所以,12==2(x+2),
解得,x=4,即OD=4.
又因为,三角形EOD的面积=三角形ACD的面积﹣梯形ACOE的面积,
所以,,
解得:y=4,即OE=4,
所以,OD=OE.
20.解:(1)由非负数的性质得:a﹣4=0,b﹣6=0,
解得a=4,b=6,
所以A(4,0),B(0,6),C(4,6);
(2)6×2÷4=3,
点P的坐标为(0,3),(4,3);
(3)14×1﹣6﹣4=4,
h=4÷2=2.
故h的值是2.
一.选择题(共9小题,满分36分)
1.平面直角坐标系中第四象限有一点P,点P到y轴的距离为2,到x轴的距离为3,则点P的坐标是( )
A.(3,﹣2) B.(﹣2,3)
C.(2,﹣3) D.(2,﹣3)或(3,﹣2)
2.若点M(a﹣2,2a+3)是y轴上的点,则a的值是( )
A.2 B.﹣ C.﹣2 D.
3.在平面直角坐标系中,若点P(a,b)在第四象限,则点Q(1+a,1﹣b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→…根据这个规律,第2020个点的坐标为( )
A.(45,5) B.(45,6) C.(45,7) D.(45,8)
5.平面直角坐标系内有点A(﹣2,3),B(4,3),则A,B相距( )
A.4个单位长度 B.5个单位长度
C.6个单位长度 D.10个单位长度
6.如图,动点P从点(3,0)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹后的路径与长方形的边的夹角为45°,第1次碰到长方形边上的点的坐标为(0,3)……第2018次碰到长方形边上的坐标为( )
A.(1,4) B.(5,0) C.(8,3) D.(7,4)
7.已知(a﹣2)2+|b+3|=0,则P(﹣a,﹣b)关于x轴对称点的坐标为( )
A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
8.在平面直角坐标系内,线段MN的两个端点坐标分别为M(﹣1,2)、N(2,1),平移线段MN得到线段M′N′,若M′的坐标为(0,1),则N′的坐标为( )
A.(3,2) B.(1,2) C.(1,0) D.(3,0)
9.若点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A.(4,﹣2) B.(3,﹣1)
C.(3,﹣1)或(3,﹣3) D.(4,﹣2)或(2,﹣2)
二.填空题(共6小题,满分30分)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
11.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)根据这个规律探索可得,第100个点的坐标为 .
12.若+(b+2)2=0,则点M(a,b)关于y轴的对称点的坐标为 .
13.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
14.已知线段AB∥x轴,AB=3,A点的坐标为(1,2),则点B的坐标为 .
15.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
三.解答题(共5小题,满分54分)
16.已知:P(4x,x﹣3)在平面直角坐标系中,
(1)若点P在第三象限的角平分线上,求x的值;
(2)若点P在第四象限,且到两坐标轴的距离之和为9,求x的值.
17.如图,在平面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求三角形ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
18.已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置;
(2)求出以A、B、C三点为顶点的三角形的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10,若存在,请直接写出点P的坐标;若不存在,请说明理由.
19.在平面直角坐标系中,A(a,b),B(2,2),且|a﹣b+8|+=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,求三角形ABC的面积;
(3)在(2)的条件下,延长AB交x轴于点D,AB交y轴于点E,那么OD与OE是否相等,请说明理由.
20.已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图所示,点P从原点出发,以每秒1个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动.
(1)写出A、B、C三点的坐标;A ,B ,C ;
(2)点P在运动过程中,当△OAP的面积为6时,求点P的坐标;
(3)当P运动14秒时,连接O、P两点,将线段OP向上平移h个单位(h>0),得到O'P',若O'P'将四边形OACB的面积分成相等的两部分,求h的值.
参考答案
一.选择题(共9小题,满分36分)
1.解:∵第四象限的点P到x轴的距离是3,到y轴的距离是2,
∴点P的横坐标是2,纵坐标是﹣3,
∴点P的坐标为(2,﹣3).故选:C.
2.解:∵点M(a﹣2,2a+3)是y轴上的点,
∴a﹣2=0,
解得:a=2,故选:A.
3.解:∵点P(a,b)在第四象限,
∴a>0,b<0,
故1+a>0,1﹣b>0,
则点Q(1+a,1﹣b)在第一象限.故选:A.
4.解:由图形可知,图中各点分别组成了正方形点阵,每个正方形点阵的整点数量依次为最右下角点横坐标的平方
且当正方形最右下角点的横坐标为奇数时,这个点可以看做按照运动方向到达x轴,当正方形最右下角点的横坐标为偶数时,这个点可以看做按照运动方向离开x轴
∵452=2025
∴第2025个点在x轴上坐标为(45,0)
则第2020个点在(45,5)故选:A.
5.解:如图,A、B间的距离为6个单位长度.
故选:C.
6.解:根据题意,如下图示:
通过上图观察可知,每碰撞6次回到始点.
∵2018÷6=336…2,
∴第2018次碰到长方形边上的点的坐标与第二次相同,即坐标为(1,4).
故选:A.
7.解:∵(a﹣2)2+|b+3|=0,
∴a=2,b=﹣3,
根据平面直角坐标系中对称点的规律可知:
点P(﹣2,3)关于x轴对称的点的坐标为(﹣2,﹣3).
故选:D.
8.解:∵点M(﹣1,2)平移后的对应点M′的坐标为(0,1),
∴线段MN的平移方向和距离为:向右平移1个单位,向下平移1个单位,
则点N(2,1)平移后的对应点N′的坐标为(3,0),
故选:D.
9.解:∵点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,MN=1,
∴y=﹣2,|x﹣3|=1,
∴x=2或4,
∴N点的坐标为(2,﹣2)或(4,﹣2).
故选:D.
二.填空题(共6小题,满分30分)
10.解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
11.解:因为1+2+3+…+13=91,所以第91个点的坐标为(13,0).
因为在第14列点的走向为向上,故第100个点在此行上,横坐标就为14,纵坐标为从第92个点向上数8个点,即为8;
故第100个点的坐标为(14,8).
故填(14,8).
12.解:∵+(b+2)2=0,
∴a=3,b=﹣2;
∴点M(a,b)关于y轴的对称点的坐标为(﹣3,﹣2).
13.解:因为点D(5,3)在边AB上,
所以AB=BC=5,BD=5﹣3=2;
(1)若把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(﹣2,0);
(2)若把△CDB逆时针旋转90°,
则点D′到x轴的距离为10,到y轴的距离为2,
所以D′(2,10),
综上,旋转后点D的对应点D′的坐标为(﹣2,0)或(2,10).
故答案为:(﹣2,0)或(2,10).
14.解:∵线段AB∥x轴,AB=3,A点的坐标为(1,2),
设点B的坐标为(b,2),
∴|1﹣b|=3,
解得,b=﹣2或b=4,
∴点B的坐标为:(﹣2,2)或(4,2),
故答案为:(﹣2,2)或(4,2).
15.解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(﹣4,3).
故答案为:(﹣4,3).
三.解答题(共5小题,满分54分)
16.解:(1)由题意,得
4x=x﹣3,
解得x=﹣1
∴点P在第三象限的角平分线上时,x=﹣1.
(2)由题意,得
4x+[﹣(x﹣3)]=9,
则3x=6,
解得x=2,此时点P的坐标为(8,﹣1),
∴当点P在第四象限,且到两坐标轴的距离之和为9时,x=2.
17.解:(1)已知点A(0,2),B(3,0),C(3,4),
过A点作BC边上的高,交BC于点H,
则三角形ABC的面积为:S=BC AH=×4×3=6;
(2)四边形ABOP的面积可以看作是△APO和△AOB的面积和,
∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO=+×(﹣m)×2=3﹣m.
故四边形ABOP的面积为3﹣m;
(3)当四边形ABOP的面积与△ABC的面积相等时,
即3﹣m=6,得m=﹣3,
此时P点坐标为:(﹣3,),
存在P点,使四边形ABOP的面积与△ABC的面积相等.
18.解:(1)描点如图;
(2)依题意,得AB∥x轴,且AB=3﹣(﹣2)=5,
∴S△ABC=×5×2=5;
(3)存在;
∵AB=5,S△ABP=10,
∴P点到AB的距离为4,
又点P在y轴上,
∴P点的坐标为(0,5)或(0,﹣3).
19.解:(1)由|a﹣b+8|+=0,得
,
解得:.
∴点A的坐标为(﹣2,6);
(2)如图1,过B作BF⊥x轴于F,三角形ABC的面积=梯形ACFB的面积﹣三角形BCF的面积
=
=(2+6)×4
=12;
(3)如图2,OD与OE相等.
理由如下:
设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y,
因为,三角形ABC的面积=三角形ACD的面积﹣三角形BCD的面积,
所以,12==2(x+2),
解得,x=4,即OD=4.
又因为,三角形EOD的面积=三角形ACD的面积﹣梯形ACOE的面积,
所以,,
解得:y=4,即OE=4,
所以,OD=OE.
20.解:(1)由非负数的性质得:a﹣4=0,b﹣6=0,
解得a=4,b=6,
所以A(4,0),B(0,6),C(4,6);
(2)6×2÷4=3,
点P的坐标为(0,3),(4,3);
(3)14×1﹣6﹣4=4,
h=4÷2=2.
故h的值是2.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
