2021-2022学年浙教版八年级数学上册第4章图形与坐标 单元综合练习(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册第4章图形与坐标 单元综合练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 294.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 08:39:56 | ||
图片预览




文档简介
2021-2022学年浙教版八年级数学上册《第4章图形与坐标》单元综合练习(附答案)
1.在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:
①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)
按照以上变换,那么f(g(a,b))等于( )
A.(﹣b,﹣a) B.(a,b) C.(b,a) D.(﹣a,﹣b)
2.如果点P(m,1﹣2m)在第四象限,那么m的取值范围是( )
A.0<m< B.﹣<m<0 C.m<0 D.m>
3.已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2021的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
4.如图,网格中的每个小正方形的边长都是1,A1、A2、A3、…都在格点上,△A1A2A3、△A3A4A5、△A5A6A7、…都是斜边在x轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若△A1A2A3的三个顶点坐标为A1(2,0)、A2(1,﹣1)、A3(0,0),则依图中规律,A19的坐标为( )
A.(10,0) B.(﹣10,0) C.(2,8) D.(﹣8,0)
5.直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数a(a>1),那么所得的图案与原来图案相比( )
A.形状不变,大小扩大到原来的a2倍 B.图案向右平移了a个单位
C.图案向上平移了a个单位 D.图案沿纵向拉长为a倍
6.点P关于x轴的对称点P1的坐标是(4,﹣8),则P点关于y轴的对称点P2的坐标是( )
A.(﹣4,﹣8) B.(﹣4,8) C.(4,8) D.(4,﹣8)
7.点A(2,﹣1)关于y轴的对称点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点M(﹣3,﹣5)向上平移7个单位到点M1的坐标为( )
A.(﹣3,2) B.(﹣2,﹣12) C.(4,﹣5) D.(﹣10,﹣5)
9.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,4),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,3) B.(﹣1,﹣3) C.(3,﹣3) D.(﹣3,﹣1)
10.已知点A关于x轴的对称点坐标为(﹣1,2),则点A关于原点的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
11.如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2022的坐标是 .
12.在平面直角坐标系中,智多星做走棋的游戏,其走法是:棋子从原点出发,第1步向上走1个单位,第2步向上走2个单位,第3步向右走1个单位,第4步向上走1个单位……依此类推,第n步的走法是:当n被3除,余数为2时,则向上走2个单位;当走完第2021步时,棋子所处位置的坐标是
13.如图中的三个点分别表示学校、图书馆、小华家,学校和图书馆分别在小华家的北偏西方向,学校又在图书馆的北偏东方向,那么图中表示图书馆的点是 .
14.已知直角坐标系中,点A(x,﹣5)与点B(1,y)关于y轴对称,则x= ,y= ;点P(m+3,m+1)在平面直角坐标系的y轴上,则P点坐标为 .
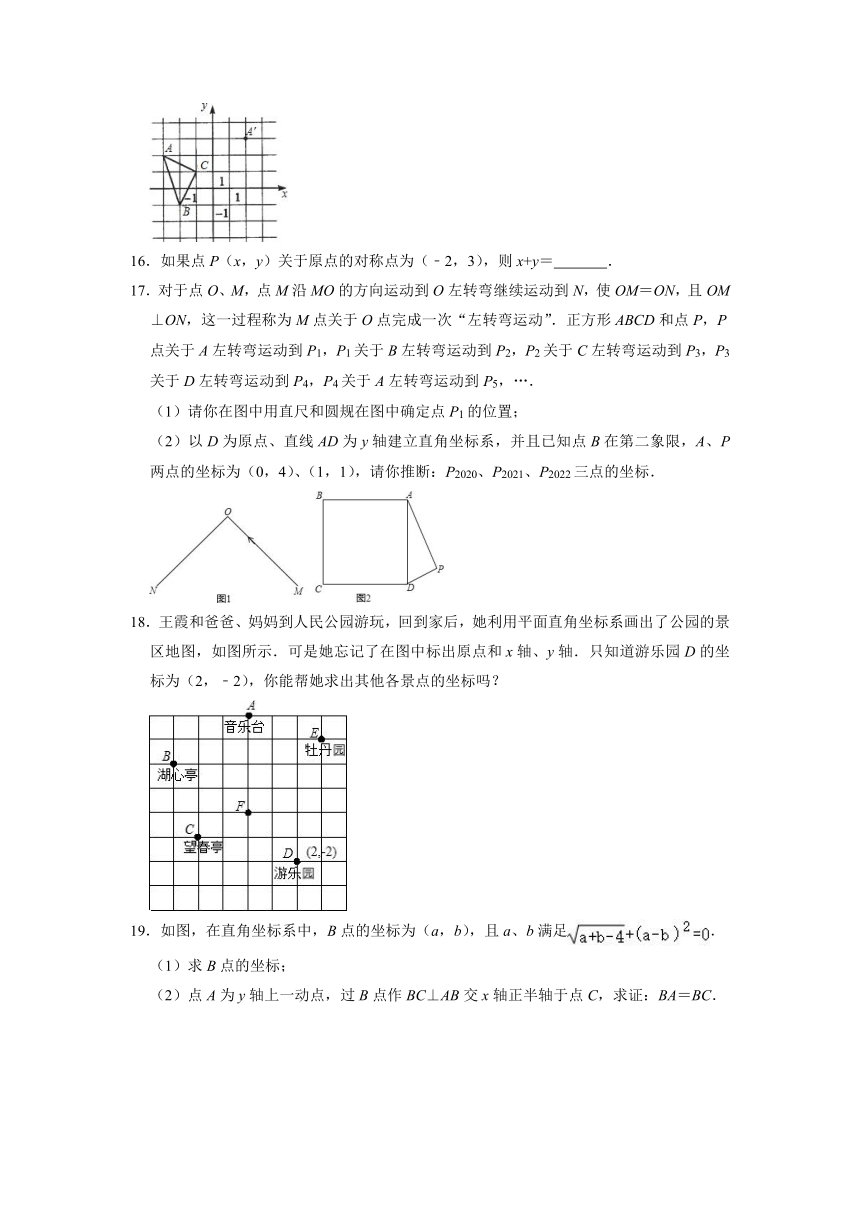
15.(经典题)如图所示,将三角形ABC,A移到A′,则B移到B′的坐标为 .C移到C′的坐标为 .
16.如果点P(x,y)关于原点的对称点为(﹣2,3),则x+y= .
17.对于点O、M,点M沿MO的方向运动到O左转弯继续运动到N,使OM=ON,且OM⊥ON,这一过程称为M点关于O点完成一次“左转弯运动”.正方形ABCD和点P,P点关于A左转弯运动到P1,P1关于B左转弯运动到P2,P2关于C左转弯运动到P3,P3关于D左转弯运动到P4,P4关于A左转弯运动到P5,….
(1)请你在图中用直尺和圆规在图中确定点P1的位置;
(2)以D为原点、直线AD为y轴建立直角坐标系,并且已知点B在第二象限,A、P两点的坐标为(0,4)、(1,1),请你推断:P2020、P2021、P2022三点的坐标.
18.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2),你能帮她求出其他各景点的坐标吗?
19.如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足.
(1)求B点的坐标;
(2)点A为y轴上一动点,过B点作BC⊥AB交x轴正半轴于点C,求证:BA=BC.
20.在直角坐标系中,△ABC满足,∠C=90°,AC=2,BC=1,点A,C分别在x轴、y轴上,当A点从原点开始在正x轴上运动时,点C随着在正y轴上运动.
(1)当A在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB;
(3)求原点O到点B的距离OB的最大值,并确定此时图形应满足什么条件?
21.如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
(1)在图中标出点M,N的位置,并分别写出点M,N的坐标: .
(2)请你依次连接M、N和第三次跳后的点,组成一个封闭的图形,并计算这个图形的面积;
(3)猜想一下,经过第2021次跳动之后,棋子将落到什么位置.
22.如图所示.
(1)写出三角形③的顶点坐标;
(2)通过平移由③能推出④吗?为什么?
(3)由对称性:由③可得①、②三角形,顶点坐标各是什么?
23.(1)在平面直角坐标系中,将点A(﹣3,4)向右平移5个单位到点A1,再将点A1绕坐标原点顺时针旋转90°到点A2.直接写出点A1,A2的坐标;
(2)在平面直角坐标系中,将第二象限内的点B(a,b)向右平移m个单位到第一象限点B1,再将点B1绕坐标原点顺时针旋转90°到点B2,直接写出点B1,B2的坐标;
(3)在平面直角坐标系中.将点P(c,d)沿水平方向平移n个单位到点P1,再将点P1绕坐标原点顺时针旋转90°到点P2,直接写出点P2的坐标.
24.在平面直角坐标系中,已知点P0的坐标为(1,0).将点P0绕着原点O按逆时针方向旋转30°得到点P1,延长OP1到点P2,使OP2=2OP1;再将点P2绕着原点O按逆时针方向旋转30°得到点P3,延长OP3到点P4,使OP4=2OP3;…如此继续下去.求:(1)点P2的坐标;(2)点P2003的坐标.
参考答案
1.解:∵g(a,b)=(b,a),
∴f(g(a,b))=f(b,a)=(﹣b,﹣a),故选A.
2.解:∵点p(m,1﹣2m)在第四象限,
∴m>0,1﹣2m<0,解得:m>,故选D.
3.解:设P1(x,y),
∵点P(0,2)关于A的对称点为P1,即A是线段PP1的中点,
∵点A(1,﹣1),
∴=1,=﹣1,解得x=2,y=﹣4,
∴P1(2,﹣4).
同理可得,P1(2,﹣4),P2(﹣4,2),P3(4,0),P4(﹣2,﹣2),P5(0,0),P6(0,2),P7(2,﹣4),…,…,
∴每6个坐标循环一次.
∵2021÷6=336…5,
∴点P2021的坐标是(0,0).
故选:A.
4.解:设到第n个三角形顶点的个数为y,
则y=2n+1,
∵当2n+1=19时,n=9,
∴A19是第9个三角形的最后一个顶点,
∵等腰直角三角形的斜边长分别为2、4、6、…,
∴第9个等腰直角三角形的斜边长为2×9=18,
由图可知,第奇数个三角形在x轴下方,关于直线x=1对称,
∴OA19=﹣1=8,
∴A19的坐标为(﹣8,0).
故选:D.
5.解:图案上各个点的横坐标和纵坐标分别乘以正数a得到的图案与原图案是以原点为位似中心,位似比为a2的位似图形,故选A.
6.解:根据轴对称的性质,得点P的坐标是(4,8),
则P点关于y轴的对称点P2的坐标是(﹣4,8).
故选:B.
7.解:∵点A与点B关于y轴对称
∴点B的坐标是(﹣2,﹣1)
∴点B在第三象限.
故选:C.
8.解:由点的平移规律可知,此题规律是(x,y+7),照此规律计算可知点M1的坐标为(﹣3,2).故选A.
9.解:横坐标从﹣2到3,说明是向右移动了3﹣(﹣2)=5,纵坐标从1到4,说明是向上移动了4﹣1=3,求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都减3.
则点B的坐标为(﹣1,﹣3).
10.解:∵点A关于x轴的对称点坐标为(﹣1,2),
∴点A坐标为(﹣1,﹣2);
∴点A关于原点的对称点的坐标为(1,2).
故选:A.
11.解:易得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵2022÷4=505…2;
∴A2022的坐标在第四象限,
横坐标为(2022﹣2)÷4+1=505;纵坐标为﹣505,
∴点A2022的坐标是(503,﹣503).
故答案为:(505,﹣505).
12.解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右1个单位,向上3个单位,
∵2021÷3=673…2,
∴走完第2021步,为第674个循环组的第2步,
所处位置的横坐标为673,
纵坐标为673×3+3=2022,
∴棋子所处位置的坐标是(673,2022).
故答案为:(673,2022).
13.解:根据题意易知C为小华家,A为学校,故图书馆是点B.
14.解:根据轴对称的性质,得x=﹣1,y=﹣5;
根据坐标轴上点的坐标特征,得m+3=0,
∴m=﹣3.
∴P点坐标为(0,﹣2).
15.解:由图中可知各点的坐标为:A(﹣3,2),B(﹣2,﹣1),C(﹣1,1).
点A横坐标从﹣3到2,说明是向右移动了2﹣(﹣3)=5个单位,纵坐标从2到3,说明是向上移动了3﹣2=1个单位,那么其余两点也遵循此规律,即点的横坐标都加5,纵坐标都加1.
则B移到B′的坐标为(3,0);C移到C′的坐标为(4,2).
故答案分别填:(3,0)、(4,2).
16.解:∵点P(x,y)关于原点的对称点为(﹣2,3),
∴x=2,y=﹣3;
∴x+y=﹣1.
17.解:(1)用直尺和圆规作图,作图痕迹清晰;
(2)点P(1,1)关于点A(0,4)左转弯运动到P1(﹣3,3),
点P1(﹣3,3)关于点B(﹣4,4)左转弯运动到点P2(﹣5,3),
点P2(﹣5,3)关于点C(﹣4,0)左转弯运动到点P3(﹣1,1),
点P3(﹣1,1)关于点D(0,0)左转弯运动到点P4(1,1),
点P4(1,1)关于点A(0,4)左转弯运动到点P5(﹣3,3),
点P5与点P1重合,点P6与点P2重合,
点P2020的坐标为(1,1),点P2021的坐标为(﹣3,3),点P2022的坐标为(﹣5,3).
18.解:由题意可知,本题是以点F为坐标原点(0,0),FA为y轴的正半轴,建立平面直角坐标系.
则A、B、C、E的坐标分别为:A(0,4);B(﹣3,2);C(﹣2,﹣1);E(3,3).
19.解:(1)∵,(a﹣b)2≥0,
而
∴,(a﹣b)2=0
∴.解得.
∴B点坐标为(2,2);
(2)作BM⊥y轴于M,BN⊥x轴于N点,如图:
∴∠MBN=90°.
∵BC⊥AB,
∴∠ABC=90°.
∴∠ABM=∠CBN.
∵B点坐标是(2,2),
∴BM=BN,
在△ABM和△CBN中,
,
∴△ABM≌△CBN(ASA).
∴BA=BC.
20.解:(1)当A点在坐标原点时,如图,
AC在y轴上,BC⊥y轴,
所以.
目的是从特殊情况理解题意,考察勾股定理的基本应用与计算.
(2)当OA=OC时,如图,△OAC是等腰直角三角形,AC=2.
所以∠1=∠2=45°,.
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
则∠3=90°﹣∠ACD=90°﹣(90°﹣45°)=45°.又BC=1,
所以,,
因此.
(3)解:如图,取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以.
在△ACB中,BC=1,,
所以.
若点O,E,B不在一条直线上,则,
若点O,E,B在一条直线上,
则,
所以当点O,E,B在一条直线上时,OB取到最大值,
最大值是.
当O,E,B在一条直线上时,OB取到最大值时,
从下图可见,OE=1,.∠CEB=45°,但CE=OE=1,
.
21.解:(1)M(﹣2,0),N(4,4);
(2)所得的三角形为PMN,且PM=2,MN=,PN=,
∴△PMN的面积=MP×NA=×5=10.
(3)棋子跳动3次后又回点P处,所以经过第2020次跳动后,棋子落在点M处,
∴经过第2021次跳动之后,棋子将落N的位置.
22.解:(1)(﹣1,﹣1),(﹣4,﹣4),(﹣3,﹣5);
(2)不能,下面两个点向右平移5个单位长度,上面一个点向右平移4个单位长度;
(3)三角形②顶点坐标为(﹣1,1),(﹣4,4),(﹣3,5);(三角形②与三角形③关于x轴对称)
三角形①顶点坐标为(1,1),(4,4),(3,5).(由③与①关于原点对称性可得①的顶点坐标)
23.解:(1)如图,∵将点A(﹣3,4)向右平移5个单位到点A1,
∴A1的坐标为(2,4),
∵又将点A1绕坐标原点顺时针旋转90°到点A2,
∴△OMA1≌△OM1A2,
∴A2的坐标(4,﹣2).
(2)根据(1)中的规律得:
B1的坐标为(a+m,b),B2的坐标为(b,﹣a﹣m).
(3)分两种情况:
①当把点P(c,d)沿水平方向右平移n个单位到点P1,
∴P1的坐标为(c+n,d),
则P2的坐标为(d,﹣c﹣n);
②当把点P(c,d)沿水平方向左平移n个单位到点P1,
∴P1的坐标为(c﹣n,d),
然后将点P1绕坐标原点顺时针旋转90°到点P2,
∴P2的坐标(d,﹣c+n).
1.在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:
①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)
按照以上变换,那么f(g(a,b))等于( )
A.(﹣b,﹣a) B.(a,b) C.(b,a) D.(﹣a,﹣b)
2.如果点P(m,1﹣2m)在第四象限,那么m的取值范围是( )
A.0<m< B.﹣<m<0 C.m<0 D.m>
3.已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2021的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
4.如图,网格中的每个小正方形的边长都是1,A1、A2、A3、…都在格点上,△A1A2A3、△A3A4A5、△A5A6A7、…都是斜边在x轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若△A1A2A3的三个顶点坐标为A1(2,0)、A2(1,﹣1)、A3(0,0),则依图中规律,A19的坐标为( )
A.(10,0) B.(﹣10,0) C.(2,8) D.(﹣8,0)
5.直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数a(a>1),那么所得的图案与原来图案相比( )
A.形状不变,大小扩大到原来的a2倍 B.图案向右平移了a个单位
C.图案向上平移了a个单位 D.图案沿纵向拉长为a倍
6.点P关于x轴的对称点P1的坐标是(4,﹣8),则P点关于y轴的对称点P2的坐标是( )
A.(﹣4,﹣8) B.(﹣4,8) C.(4,8) D.(4,﹣8)
7.点A(2,﹣1)关于y轴的对称点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点M(﹣3,﹣5)向上平移7个单位到点M1的坐标为( )
A.(﹣3,2) B.(﹣2,﹣12) C.(4,﹣5) D.(﹣10,﹣5)
9.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,4),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,3) B.(﹣1,﹣3) C.(3,﹣3) D.(﹣3,﹣1)
10.已知点A关于x轴的对称点坐标为(﹣1,2),则点A关于原点的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
11.如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2022的坐标是 .
12.在平面直角坐标系中,智多星做走棋的游戏,其走法是:棋子从原点出发,第1步向上走1个单位,第2步向上走2个单位,第3步向右走1个单位,第4步向上走1个单位……依此类推,第n步的走法是:当n被3除,余数为2时,则向上走2个单位;当走完第2021步时,棋子所处位置的坐标是
13.如图中的三个点分别表示学校、图书馆、小华家,学校和图书馆分别在小华家的北偏西方向,学校又在图书馆的北偏东方向,那么图中表示图书馆的点是 .
14.已知直角坐标系中,点A(x,﹣5)与点B(1,y)关于y轴对称,则x= ,y= ;点P(m+3,m+1)在平面直角坐标系的y轴上,则P点坐标为 .
15.(经典题)如图所示,将三角形ABC,A移到A′,则B移到B′的坐标为 .C移到C′的坐标为 .
16.如果点P(x,y)关于原点的对称点为(﹣2,3),则x+y= .
17.对于点O、M,点M沿MO的方向运动到O左转弯继续运动到N,使OM=ON,且OM⊥ON,这一过程称为M点关于O点完成一次“左转弯运动”.正方形ABCD和点P,P点关于A左转弯运动到P1,P1关于B左转弯运动到P2,P2关于C左转弯运动到P3,P3关于D左转弯运动到P4,P4关于A左转弯运动到P5,….
(1)请你在图中用直尺和圆规在图中确定点P1的位置;
(2)以D为原点、直线AD为y轴建立直角坐标系,并且已知点B在第二象限,A、P两点的坐标为(0,4)、(1,1),请你推断:P2020、P2021、P2022三点的坐标.
18.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2),你能帮她求出其他各景点的坐标吗?
19.如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足.
(1)求B点的坐标;
(2)点A为y轴上一动点,过B点作BC⊥AB交x轴正半轴于点C,求证:BA=BC.
20.在直角坐标系中,△ABC满足,∠C=90°,AC=2,BC=1,点A,C分别在x轴、y轴上,当A点从原点开始在正x轴上运动时,点C随着在正y轴上运动.
(1)当A在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB;
(3)求原点O到点B的距离OB的最大值,并确定此时图形应满足什么条件?
21.如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
(1)在图中标出点M,N的位置,并分别写出点M,N的坐标: .
(2)请你依次连接M、N和第三次跳后的点,组成一个封闭的图形,并计算这个图形的面积;
(3)猜想一下,经过第2021次跳动之后,棋子将落到什么位置.
22.如图所示.
(1)写出三角形③的顶点坐标;
(2)通过平移由③能推出④吗?为什么?
(3)由对称性:由③可得①、②三角形,顶点坐标各是什么?
23.(1)在平面直角坐标系中,将点A(﹣3,4)向右平移5个单位到点A1,再将点A1绕坐标原点顺时针旋转90°到点A2.直接写出点A1,A2的坐标;
(2)在平面直角坐标系中,将第二象限内的点B(a,b)向右平移m个单位到第一象限点B1,再将点B1绕坐标原点顺时针旋转90°到点B2,直接写出点B1,B2的坐标;
(3)在平面直角坐标系中.将点P(c,d)沿水平方向平移n个单位到点P1,再将点P1绕坐标原点顺时针旋转90°到点P2,直接写出点P2的坐标.
24.在平面直角坐标系中,已知点P0的坐标为(1,0).将点P0绕着原点O按逆时针方向旋转30°得到点P1,延长OP1到点P2,使OP2=2OP1;再将点P2绕着原点O按逆时针方向旋转30°得到点P3,延长OP3到点P4,使OP4=2OP3;…如此继续下去.求:(1)点P2的坐标;(2)点P2003的坐标.
参考答案
1.解:∵g(a,b)=(b,a),
∴f(g(a,b))=f(b,a)=(﹣b,﹣a),故选A.
2.解:∵点p(m,1﹣2m)在第四象限,
∴m>0,1﹣2m<0,解得:m>,故选D.
3.解:设P1(x,y),
∵点P(0,2)关于A的对称点为P1,即A是线段PP1的中点,
∵点A(1,﹣1),
∴=1,=﹣1,解得x=2,y=﹣4,
∴P1(2,﹣4).
同理可得,P1(2,﹣4),P2(﹣4,2),P3(4,0),P4(﹣2,﹣2),P5(0,0),P6(0,2),P7(2,﹣4),…,…,
∴每6个坐标循环一次.
∵2021÷6=336…5,
∴点P2021的坐标是(0,0).
故选:A.
4.解:设到第n个三角形顶点的个数为y,
则y=2n+1,
∵当2n+1=19时,n=9,
∴A19是第9个三角形的最后一个顶点,
∵等腰直角三角形的斜边长分别为2、4、6、…,
∴第9个等腰直角三角形的斜边长为2×9=18,
由图可知,第奇数个三角形在x轴下方,关于直线x=1对称,
∴OA19=﹣1=8,
∴A19的坐标为(﹣8,0).
故选:D.
5.解:图案上各个点的横坐标和纵坐标分别乘以正数a得到的图案与原图案是以原点为位似中心,位似比为a2的位似图形,故选A.
6.解:根据轴对称的性质,得点P的坐标是(4,8),
则P点关于y轴的对称点P2的坐标是(﹣4,8).
故选:B.
7.解:∵点A与点B关于y轴对称
∴点B的坐标是(﹣2,﹣1)
∴点B在第三象限.
故选:C.
8.解:由点的平移规律可知,此题规律是(x,y+7),照此规律计算可知点M1的坐标为(﹣3,2).故选A.
9.解:横坐标从﹣2到3,说明是向右移动了3﹣(﹣2)=5,纵坐标从1到4,说明是向上移动了4﹣1=3,求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都减3.
则点B的坐标为(﹣1,﹣3).
10.解:∵点A关于x轴的对称点坐标为(﹣1,2),
∴点A坐标为(﹣1,﹣2);
∴点A关于原点的对称点的坐标为(1,2).
故选:A.
11.解:易得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵2022÷4=505…2;
∴A2022的坐标在第四象限,
横坐标为(2022﹣2)÷4+1=505;纵坐标为﹣505,
∴点A2022的坐标是(503,﹣503).
故答案为:(505,﹣505).
12.解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右1个单位,向上3个单位,
∵2021÷3=673…2,
∴走完第2021步,为第674个循环组的第2步,
所处位置的横坐标为673,
纵坐标为673×3+3=2022,
∴棋子所处位置的坐标是(673,2022).
故答案为:(673,2022).
13.解:根据题意易知C为小华家,A为学校,故图书馆是点B.
14.解:根据轴对称的性质,得x=﹣1,y=﹣5;
根据坐标轴上点的坐标特征,得m+3=0,
∴m=﹣3.
∴P点坐标为(0,﹣2).
15.解:由图中可知各点的坐标为:A(﹣3,2),B(﹣2,﹣1),C(﹣1,1).
点A横坐标从﹣3到2,说明是向右移动了2﹣(﹣3)=5个单位,纵坐标从2到3,说明是向上移动了3﹣2=1个单位,那么其余两点也遵循此规律,即点的横坐标都加5,纵坐标都加1.
则B移到B′的坐标为(3,0);C移到C′的坐标为(4,2).
故答案分别填:(3,0)、(4,2).
16.解:∵点P(x,y)关于原点的对称点为(﹣2,3),
∴x=2,y=﹣3;
∴x+y=﹣1.
17.解:(1)用直尺和圆规作图,作图痕迹清晰;
(2)点P(1,1)关于点A(0,4)左转弯运动到P1(﹣3,3),
点P1(﹣3,3)关于点B(﹣4,4)左转弯运动到点P2(﹣5,3),
点P2(﹣5,3)关于点C(﹣4,0)左转弯运动到点P3(﹣1,1),
点P3(﹣1,1)关于点D(0,0)左转弯运动到点P4(1,1),
点P4(1,1)关于点A(0,4)左转弯运动到点P5(﹣3,3),
点P5与点P1重合,点P6与点P2重合,
点P2020的坐标为(1,1),点P2021的坐标为(﹣3,3),点P2022的坐标为(﹣5,3).
18.解:由题意可知,本题是以点F为坐标原点(0,0),FA为y轴的正半轴,建立平面直角坐标系.
则A、B、C、E的坐标分别为:A(0,4);B(﹣3,2);C(﹣2,﹣1);E(3,3).
19.解:(1)∵,(a﹣b)2≥0,
而
∴,(a﹣b)2=0
∴.解得.
∴B点坐标为(2,2);
(2)作BM⊥y轴于M,BN⊥x轴于N点,如图:
∴∠MBN=90°.
∵BC⊥AB,
∴∠ABC=90°.
∴∠ABM=∠CBN.
∵B点坐标是(2,2),
∴BM=BN,
在△ABM和△CBN中,
,
∴△ABM≌△CBN(ASA).
∴BA=BC.
20.解:(1)当A点在坐标原点时,如图,
AC在y轴上,BC⊥y轴,
所以.
目的是从特殊情况理解题意,考察勾股定理的基本应用与计算.
(2)当OA=OC时,如图,△OAC是等腰直角三角形,AC=2.
所以∠1=∠2=45°,.
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
则∠3=90°﹣∠ACD=90°﹣(90°﹣45°)=45°.又BC=1,
所以,,
因此.
(3)解:如图,取AC的中点E,连接OE,BE.在Rt△AOC中,OE是斜边AC上的中线,所以.
在△ACB中,BC=1,,
所以.
若点O,E,B不在一条直线上,则,
若点O,E,B在一条直线上,
则,
所以当点O,E,B在一条直线上时,OB取到最大值,
最大值是.
当O,E,B在一条直线上时,OB取到最大值时,
从下图可见,OE=1,.∠CEB=45°,但CE=OE=1,
.
21.解:(1)M(﹣2,0),N(4,4);
(2)所得的三角形为PMN,且PM=2,MN=,PN=,
∴△PMN的面积=MP×NA=×5=10.
(3)棋子跳动3次后又回点P处,所以经过第2020次跳动后,棋子落在点M处,
∴经过第2021次跳动之后,棋子将落N的位置.
22.解:(1)(﹣1,﹣1),(﹣4,﹣4),(﹣3,﹣5);
(2)不能,下面两个点向右平移5个单位长度,上面一个点向右平移4个单位长度;
(3)三角形②顶点坐标为(﹣1,1),(﹣4,4),(﹣3,5);(三角形②与三角形③关于x轴对称)
三角形①顶点坐标为(1,1),(4,4),(3,5).(由③与①关于原点对称性可得①的顶点坐标)
23.解:(1)如图,∵将点A(﹣3,4)向右平移5个单位到点A1,
∴A1的坐标为(2,4),
∵又将点A1绕坐标原点顺时针旋转90°到点A2,
∴△OMA1≌△OM1A2,
∴A2的坐标(4,﹣2).
(2)根据(1)中的规律得:
B1的坐标为(a+m,b),B2的坐标为(b,﹣a﹣m).
(3)分两种情况:
①当把点P(c,d)沿水平方向右平移n个单位到点P1,
∴P1的坐标为(c+n,d),
则P2的坐标为(d,﹣c﹣n);
②当把点P(c,d)沿水平方向左平移n个单位到点P1,
∴P1的坐标为(c﹣n,d),
然后将点P1绕坐标原点顺时针旋转90°到点P2,
∴P2的坐标(d,﹣c+n).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
